Wenn die Anzahl der Schlitze in einem Hindernis groß ist, wird die Schärfe des Musters verbessert, die Maxima werden schmaler. Hindernisse mit einer großen Anzahl von Schlitzen (mehr als, sagen wir, 20 auf den Millimeter) werden Beugungsgitter genannt. Diese wurden erstmals von Fraunhofer im späten 18. Jahrhundert entwickelt und bestanden aus feinem Silberdraht, der auf zwei parallele Schrauben gewickelt war und etwa 30 Hindernisse pro Millimeter ergab.
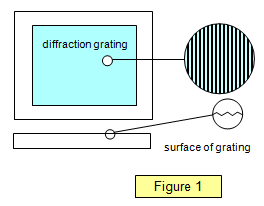
Seitdem wurden viele Verbesserungen vorgenommen, 1882 benutzte Rowland einen Diamanten, um feine Linien auf Glas zu zeichnen, wobei die Grate als Schlitze und die Lineale als Hindernisse fungierten (siehe Abbildung 1). Mit dieser Methode ist es möglich, Beugungsgitter mit bis zu 3000 Linien pro Millimeter zu erhalten, obwohl „grobe“ Gitter mit etwa 500 Linien pro Millimeter für den allgemeinen Gebrauch besser geeignet sind.
In vielen Schulen sind zwei Typen in Gebrauch, einer mit 300 Linien pro mm und der andere mit 80 Linien pro mm.
Es werden auch Reflexionsgitter verwendet, bei denen das gebeugte Bild nach der Reflexion an einer linierten Oberfläche betrachtet wird. Ein sehr gutes Beispiel für ein Reflexionsbeugungsgitter ist eine CD. Eine DVD mit feineren Linien ergibt ein viel breiteres Beugungsmuster.
Die Wellentheorie und das Beugungsgitter
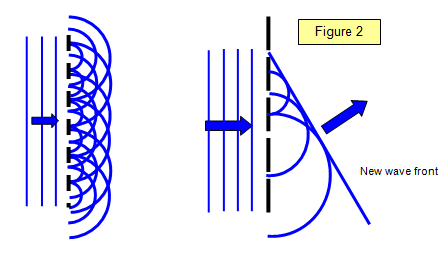
Abbildung 2 zeigt die Huygens-Konstruktion für ein Gitter. Man sieht, wie sich die kreisförmigen gebeugten Wellen von jedem Spalt in bestimmten Richtungen zu einer gebeugten Welle addieren, die eine ebene Wellenfront hat, genau wie die Wellen, die von links auf das Gitter treffen. Diese ebene Welle entsteht durch das Ziehen der Linie, die alle kleinen Kreiswellen trifft, und wird Hüllkurve all dieser kleinen Sekundärwellen genannt.
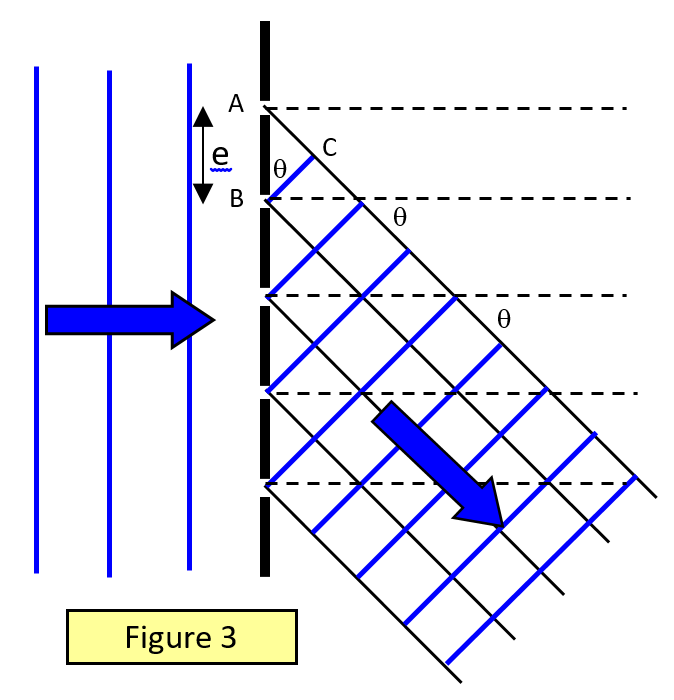
Die Beugungsgitterformel
Betrachten Sie einen parallelen Lichtstrahl, der normal auf ein Beugungsgitter mit einem Gitterabstand e einfällt (der Gitterabstand ist der Kehrwert der Anzahl der Linien pro Längeneinheit). Betrachten Sie Licht, das unter einem Winkel q zur Normalen gebeugt wird und von entsprechenden Punkten auf benachbarten Schlitzen kommt (Abbildung 3).
Für ein Maximum ist die Wegdifferenz = AC = mλ
Aber AC = e sinθ. Daher gilt für ein Maximum:
mλ = e sinθ
mit m = 0, 1, 2,3…
Die Zahl m wird als Ordnung des Spektrums bezeichnet, d.h. für m = 1 entsteht ein Spektrum erster Ordnung usw.
Wird Licht einer einzigen Wellenlänge, wie z.B. das eines Lasers, verwendet, so entsteht eine Reihe von scharfen Linien, eine Linie für jede Ordnung des Spektrums. Bei einer weißen Lichtquelle entsteht eine Reihe von Spektren, wobei das Licht mit der kürzesten Wellenlänge den kleinsten Beugungswinkel hat.
Bei der Herleitung der obigen Formel wurde angenommen, dass der einfallende Strahl rechtwinklig zur Fläche des Gitters steht. Wenn dies nicht der Fall ist, muss eine Korrektur vorgenommen werden. Der einfachste Weg ist, die Position des Spektrums erster Ordnung auf beiden Seiten des Zentrums zu messen, den Winkel zwischen diesen Positionen aufzuzeichnen und ihn dann zu halbieren, wie in Abbildung 4 gezeigt.
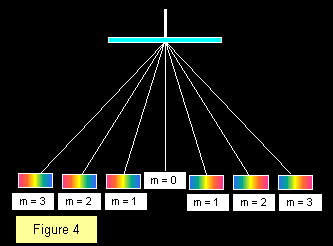
Die Anzahl der Ordnungen von Spektren, die mit einem gegebenen Gitter sichtbar sind, hängt vom Gitterabstand ab, wobei mehr Spektren bei gröberen Gittern sichtbar sind. Die linierte Fläche des Gitters sollte immer vom einfallenden Licht weg zeigen, um Fehler durch Richtungsänderungen aufgrund von Brechung im Glas zu vermeiden. Das Diagramm zeigt einen zentralen weißen Streifen mit drei Spektren auf jeder Seite, was insgesamt sieben Bilder ergibt.
(Siehe Beispielproblem )
1. Berechnen Sie die Wellenlänge des monochromatischen Lichts, an dem das Bild zweiter Ordnung unter einem Winkel von 25o gebeugt wird, unter Verwendung eines Beugungsgitters mit 300 Linien pro Millimeter.
Gitterabstand (e) = 10-3/300 m = 3.3×10-6 m
Wellenlänge (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Berechnen Sie die maximale Anzahl der sichtbaren Ordnungen bei einem Beugungsgitter mit 500 Linien pro Millimeter mit Licht der Wellenlänge 600 nm.
Maximaler Beugungswinkel = 90o e = 10-3/500 = 2×10-6 m
Daher m = esinq/l = 2×10-6/600×10-9 = 3,33
Daher maximale Anzahl der Ordnungen = 3, und es sind insgesamt sieben Bilder der Quelle zu sehen (drei auf jeder Seite eines zentralen Bildes).
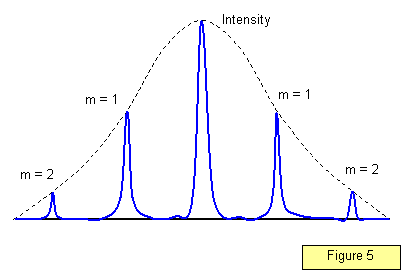
Die Intensitätsverteilung im Beugungsmuster für eine große Anzahl von Schlitzen ist in Abbildung 5 dargestellt. Beachten Sie, dass die Maxima viel schärfer werden; je größer die Anzahl der Schlitze pro Meter ist, desto besser sind die Maxima definiert.
Die Beugung von Cadmium- oder Quecksilberlicht wird verwendet, um den Abstand zweier Linien auf einer integrierten Schaltung zu bestimmen. Die folgenden Ergebnisse wurden für die Beugungsbilder zweiter Ordnung für verschiedene Wellenlängen erhalten. Verwenden Sie diese, um einen entsprechenden linearen Graphen zu zeichnen und daraus den mittleren Abstand der Leitungen auf der Schaltung zu bestimmen.
| Wellenlänge/nm | Brechungswinkel (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40.0 |