![]()
![]()

Die Binomialverteilung gibt die diskrete Wahrscheinlichkeitsverteilung ![]() des Erhalts von genau
des Erhalts von genau ![]() Erfolgen aus
Erfolgen aus ![]() Bernoulli-Versuchen (wobei das Ergebnis jedes Bernoulli-Versuchs mit Wahrscheinlichkeit
Bernoulli-Versuchen (wobei das Ergebnis jedes Bernoulli-Versuchs mit Wahrscheinlichkeit ![]() wahr und mit Wahrscheinlichkeit
wahr und mit Wahrscheinlichkeit ![]() ). Die Binomialverteilung ist also gegeben durch
). Die Binomialverteilung ist also gegeben durch
|
(1)
|
|||
|
(2)
|
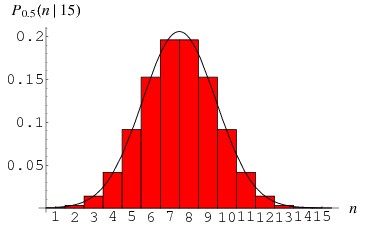
wobei ![]() ein Binomialkoeffizient ist. Die obige Darstellung zeigt die Verteilung von
ein Binomialkoeffizient ist. Die obige Darstellung zeigt die Verteilung von ![]() Erfolgen aus
Erfolgen aus ![]() Versuchen mit
Versuchen mit ![]() .
.
Die Binomialverteilung ist in der Wolfram Language als BinomialDistribution implementiert.
Die Wahrscheinlichkeit, mehr Erfolge als das ![]() zu erhalten, ist bei einer Binomialverteilung
zu erhalten, ist bei einer Binomialverteilung
|
(3)
|
wobei
|
(4)
|
![]() ist die Beta-Funktion, und
ist die Beta-Funktion, und ![]() ist die unvollständige Betafunktion.
ist die unvollständige Betafunktion.
Die charakteristische Funktion für die Binomialverteilung ist
|
(5)
|
(Papoulis 1984, p. 154). Die moment-erzeugende Funktion ![]() für die Verteilung ist
für die Verteilung ist
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
Der Mittelwert ist
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
Die Momente um 0 sind
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
so sind die Momente um den Mittelwert
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
Die Schiefe und Kurtosisexzess sind
|
(22)
|
|||
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
Der erste Kumulant ist
|
(26)
|
und die nachfolgenden Kumulanten sind gegeben durch die Rekursionsbeziehung
|
(27)
|
Die mittlere Abweichung ist gegeben durch
|
(28)
|
Für den Spezialfall ![]() , ist dies gleich
, ist dies gleich
|
(29)
|
|||
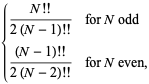 |
(30)
|
wobei ![]() eine doppelte Fakultät ist. Für
eine doppelte Fakultät ist. Für ![]() , 2, … sind die ersten paar Werte also 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 und A086117). Der allgemeine Fall ist gegeben durch
, 2, … sind die ersten paar Werte also 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 und A086117). Der allgemeine Fall ist gegeben durch
|
(31)
|
Steinhaus (1999, pp. 25-28) betrachtet die erwartete Anzahl von Quadraten ![]() , die eine gegebene Anzahl von Körnern
, die eine gegebene Anzahl von Körnern ![]() auf einem Brett der Größe
auf einem Brett der Größe ![]() nach einer Zufallsverteilung von
nach einer Zufallsverteilung von ![]() von Körnern enthalten,
von Körnern enthalten,
|
(32)
|
Nimmt man ![]() , erhält man die in der folgenden Tabelle zusammengefassten Ergebnisse.
, erhält man die in der folgenden Tabelle zusammengefassten Ergebnisse.
| 0 | 23.3591 |
| 1 | 23.7299 |
| 2 | 11.8650 |
| 3 | 3.89221 |
| 4 | 0.942162 |
| 5 | 0.179459 |
| 6 | 0.0280109 |
| 7 | 0.0036840 |
| 8 | |
| 9 | |
| 10 | |
Eine Approximation der Binomialverteilung für große ![]() kann durch Expansion um den Wert
kann durch Expansion um den Wert ![]() erhalten werden, wobei
erhalten werden, wobei ![]() ein Maximum ist, i.e., wobei
ein Maximum ist, i.e., wobei ![]() . Da die Logarithmusfunktion monoton ist, können wir stattdessen die Erweiterung des Logarithmus wählen. Sei
. Da die Logarithmusfunktion monoton ist, können wir stattdessen die Erweiterung des Logarithmus wählen. Sei ![]() , dann
, dann
|
(33)
|
wo
|
(34)
|
Aber wir expandieren um das Maximum, also, per Definition,
|
(35)
|
Das bedeutet auch, dass ![]() negativ ist, also können wir schreiben
negativ ist, also können wir schreiben ![]() . Wenn man nun den Logarithmus von (◇) nimmt, erhält man
. Wenn man nun den Logarithmus von (◇) nimmt, erhält man
|
(36)
|
Für große ![]() und
und ![]() können wir die Stirlingsche Näherung verwenden
können wir die Stirlingsche Näherung verwenden
|
(37)
|
so
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
|||
|
(41)
|
|||
|
(42)
|
und
|
(43)
|
Um ![]() zu finden, setzen Sie diesen Ausdruck auf 0 und lösen Sie für
zu finden, setzen Sie diesen Ausdruck auf 0 und lösen Sie für ![]() ,
,
|
(44)
|
|
(45)
|
|
(46)
|
|
(47)
|
da ![]() . Wir können nun die Terme in der Erweiterung finden
. Wir können nun die Terme in der Erweiterung finden
|
(48)
|
|||
|
(49)
|
|||
|
(50)
|
|||
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
|||
|
(55)
|
|||
|
(56)
|
|||
|
(57)
|
|||
|
(58)
|
|||
|
(59)
|
Nun behandeln wir die Verteilung als kontinuierlich,
|
(60)
|
Da jeder Term der Ordnung ![]() kleiner ist als der vorherige, können wir Terme höher als
kleiner ist als der vorherige, können wir Terme höher als ![]() ignorieren, also
ignorieren, also
|
(61)
|
Die Wahrscheinlichkeit muss normiert werden, also
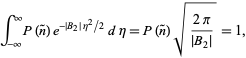 |
(62)
|
und
|
(63)
|
|||
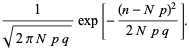 |
(64)
|
Definieren von ![]() ,
,
|
(65)
|
Das ist eine Normalverteilung. Die Binomialverteilung wird also für jedes feste ![]() (auch wenn
(auch wenn ![]() klein ist) durch eine Normalverteilung approximiert, wenn
klein ist) durch eine Normalverteilung approximiert, wenn ![]() auf unendlich gesetzt wird.
auf unendlich gesetzt wird.
Wenn ![]() und
und ![]() so sind, dass
so sind, dass ![]() , dann konvergiert die Binomialverteilung gegen die Poisson-Verteilung mit Mittelwert
, dann konvergiert die Binomialverteilung gegen die Poisson-Verteilung mit Mittelwert ![]() .
.
Lassen Sie ![]() und
und ![]() unabhängige binomiale Zufallsvariablen sein, die durch die Parameter
unabhängige binomiale Zufallsvariablen sein, die durch die Parameter ![]() und
und ![]() gekennzeichnet sind. Die bedingte Wahrscheinlichkeit von
gekennzeichnet sind. Die bedingte Wahrscheinlichkeit von ![]() bei
bei ![]() ist
ist
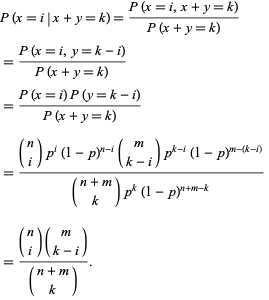 |
(66)
|
Beachten Sie, dass dies eine hypergeometrische Verteilung ist.