Das Interesse an maschinellem Lernen ist in den letzten Jahren sprunghaft angestiegen, seit ein Artikel der Harvard Business Review den „Data Scientist“ zum „sexiesten Job des 21. Jahrhunderts“ erklärt hat. Aber wenn Sie gerade erst mit dem maschinellen Lernen beginnen, kann der Einstieg etwas schwierig sein. Deshalb haben wir unseren immens beliebten Beitrag über gute Machine-Learning-Algorithmen für Anfänger neu aufgelegt.
(Dieser Beitrag wurde ursprünglich auf KDNuggets als The 10 Algorithms Machine Learning Engineers Need to Know veröffentlicht. Er wurde mit Erlaubnis erneut gepostet und zuletzt 2019 aktualisiert).
Dieser Post richtet sich an Anfänger. Wenn Sie schon etwas Erfahrung mit Data Science und maschinellem Lernen haben, sind Sie vielleicht mehr an diesem tiefergehenden Tutorial über maschinelles Lernen in Python mit scikit-learn oder an unseren Kursen zum maschinellen Lernen interessiert, die hier beginnen. Wenn Sie sich über die Unterschiede zwischen „Data Science“ und „Machine Learning“ noch nicht im Klaren sind, bietet dieser Artikel eine gute Erklärung: Maschinelles Lernen und Data Science – was unterscheidet sie?
Maschinelle Lernalgorithmen sind Programme, die aus Daten lernen und sich durch Erfahrung verbessern können, ohne dass ein Mensch eingreifen muss. Zu den Lernaufgaben gehören das Lernen der Funktion, die die Eingabe auf die Ausgabe abbildet, das Lernen der versteckten Struktur in unbeschrifteten Daten oder das „instanzbasierte Lernen“, bei dem ein Klassenlabel für eine neue Instanz erzeugt wird, indem die neue Instanz (Zeile) mit Instanzen aus den Trainingsdaten verglichen wird, die im Speicher abgelegt wurden.
Typen von Algorithmen des maschinellen Lernens
Es gibt 3 Arten von Algorithmen des maschinellen Lernens (ML):
Überwachte Lernalgorithmen:
Überwachtes Lernen verwendet markierte Trainingsdaten, um die Abbildungsfunktion zu lernen, die Eingabevariablen (X) in die Ausgabevariable (Y) umwandelt. Mit anderen Worten, es löst f in der folgenden Gleichung:
Dadurch können wir bei neuen Eingaben präzise Ausgaben generieren.
Wir werden über zwei Arten des überwachten Lernens sprechen: Klassifizierung und Regression.
Die Klassifizierung wird verwendet, um das Ergebnis einer gegebenen Probe vorherzusagen, wenn die Ausgabevariable in Form von Kategorien vorliegt. Ein Klassifizierungsmodell könnte sich die Eingabedaten ansehen und versuchen, Bezeichnungen wie „krank“ oder „gesund“ vorherzusagen.
Regression wird verwendet, um das Ergebnis einer gegebenen Stichprobe vorherzusagen, wenn die Ausgabevariable in Form von realen Werten vorliegt. Zum Beispiel könnte ein Regressionsmodell Eingabedaten verarbeiten, um die Menge des Niederschlags, die Größe einer Person usw. vorherzusagen.
Die ersten 5 Algorithmen, die wir in diesem Blog behandeln – Lineare Regression, Logistische Regression, CART, Naïve-Bayes und K-Nearest Neighbors (KNN) – sind Beispiele für überwachtes Lernen.
Ensembling ist eine weitere Art des überwachten Lernens. Es bedeutet, dass die Vorhersagen mehrerer maschineller Lernmodelle, die einzeln schwach sind, kombiniert werden, um eine genauere Vorhersage für eine neue Probe zu erhalten. Die Algorithmen 9 und 10 dieses Artikels – Bagging mit Random Forests, Boosting mit XGBoost – sind Beispiele für Ensemble-Techniken.
Unüberwachte Lernalgorithmen:
Unüberwachte Lernmodelle werden verwendet, wenn wir nur die Eingabevariablen (X) und keine entsprechenden Ausgabevariablen haben. Sie verwenden unmarkierte Trainingsdaten, um die zugrundeliegende Struktur der Daten zu modellieren.
Wir werden über drei Arten des unüberwachten Lernens sprechen:
Assoziation wird verwendet, um die Wahrscheinlichkeit des gemeinsamen Auftretens von Elementen in einer Sammlung zu entdecken. Sie wird häufig in der Warenkorbanalyse verwendet. Beispielsweise könnte ein Assoziationsmodell verwendet werden, um herauszufinden, dass ein Kunde, der Brot kauft, mit 80-prozentiger Wahrscheinlichkeit auch Eier kauft.
Clustering wird verwendet, um Stichproben so zu gruppieren, dass Objekte innerhalb desselben Clusters einander ähnlicher sind als den Objekten aus einem anderen Cluster.
Dimensionalitätsreduktion wird verwendet, um die Anzahl der Variablen eines Datensatzes zu reduzieren und gleichzeitig sicherzustellen, dass wichtige Informationen weiterhin vermittelt werden. Die Dimensionalitätsreduktion kann mit Methoden der Feature-Extraktion und der Feature-Selektion durchgeführt werden. Bei der Merkmalsauswahl wird eine Teilmenge der ursprünglichen Variablen ausgewählt. Die Feature-Extraktion führt eine Datentransformation von einem hochdimensionalen Raum in einen niedrigdimensionalen Raum durch. Beispiel: PCA-Algorithmus ist ein Feature-Extraktions-Ansatz.
Die hier behandelten Algorithmen 6-8 – Apriori, K-means, PCA – sind Beispiele für unüberwachtes Lernen.
Verstärkungslernen:
Verstärkungslernen ist eine Art von maschinellem Lernalgorithmus, der es einem Agenten ermöglicht, die beste nächste Aktion basierend auf seinem aktuellen Zustand zu entscheiden, indem er Verhaltensweisen lernt, die eine Belohnung maximieren.
Verstärkungsalgorithmen lernen optimale Aktionen normalerweise durch Versuch und Irrtum. Stellen Sie sich zum Beispiel ein Videospiel vor, in dem sich der Spieler zu bestimmten Zeiten an bestimmte Orte bewegen muss, um Punkte zu erhalten. Ein Verstärkungsalgorithmus, der dieses Spiel spielt, würde sich anfangs zufällig bewegen, aber mit der Zeit durch Versuch und Irrtum lernen, wo und wann er die Spielfigur bewegen muss, um seine Punktzahl zu maximieren.
Quantifizierung der Popularität von Algorithmen für maschinelles Lernen
Woher haben wir diese zehn Algorithmen? Jede solche Liste ist von Natur aus subjektiv. Studien wie diese haben die 10 beliebtesten Data-Mining-Algorithmen quantifiziert, aber sie verlassen sich immer noch auf die subjektiven Antworten von Befragten, meist fortgeschrittenen akademischen Praktikern. In der oben verlinkten Studie wurden beispielsweise die Gewinner des ACM KDD Innovation Award, des IEEE ICDM Research Contributions Award, die Mitglieder des Programmkomitees der KDD ’06, ICDM ’06 und SDM ’06 sowie die 145 Teilnehmer der ICDM ’06 befragt.
Die in diesem Beitrag aufgelisteten Top-10-Algorithmen wurden mit Blick auf Machine Learning-Anfänger ausgewählt. Es handelt sich hauptsächlich um Algorithmen, die ich im Kurs „Data Warehousing and Mining“ (DWM) während meines Bachelor-Studiums in Computer Engineering an der Universität von Mumbai gelernt habe. Die letzten beiden Algorithmen (Ensemble-Methoden) habe ich vor allem deshalb aufgenommen, weil sie häufig verwendet werden, um Kaggle-Wettbewerbe zu gewinnen.
Ohne weitere Umschweife, die Top 10 Machine Learning Algorithmen für Einsteiger:
1. Lineare Regression
Beim maschinellen Lernen haben wir einen Satz von Eingabevariablen (x), die zur Bestimmung einer Ausgabevariablen (y) verwendet werden. Es besteht eine Beziehung zwischen den Eingabevariablen und der Ausgabevariablen. Das Ziel von ML ist es, diese Beziehung zu quantifizieren.

Bei der linearen Regression wird die Beziehung zwischen den Eingangsvariablen (x) und der Ausgangsvariablen (y) als Gleichung der Form y = a + bx dargestellt. Das Ziel der linearen Regression ist es also, die Werte der Koeffizienten a und b herauszufinden. Dabei ist a der Achsenabschnitt und b die Steigung der Linie.
Abbildung 1 zeigt die aufgetragenen x- und y-Werte für einen Datensatz. Das Ziel ist es, eine Linie anzupassen, die den meisten Punkten am nächsten kommt. Dies würde den Abstand („Fehler“) zwischen dem y-Wert eines Datenpunktes und der Linie verringern.
2. logistische Regression
Die Vorhersagen der linearen Regression sind kontinuierliche Werte (z.B. Regenmenge in cm), die Vorhersagen der logistischen Regression sind diskrete Werte (z.B., ob ein Schüler bestanden/nicht bestanden hat) nach Anwendung einer Transformationsfunktion.
Die logistische Regression eignet sich am besten für binäre Klassifizierung: Datensätze, bei denen y = 0 oder 1 ist, wobei 1 die Standardklasse bezeichnet. Bei der Vorhersage, ob ein Ereignis eintritt oder nicht, gibt es zum Beispiel nur zwei Möglichkeiten: dass es eintritt (was wir als 1 bezeichnen) oder dass es nicht eintritt (0). Wenn wir also vorhersagen würden, ob ein Patient krank ist, würden wir kranke Patienten mit dem Wert von 1 in unserem Datensatz kennzeichnen.
Die logistische Regression ist nach der Transformationsfunktion benannt, die sie verwendet, nämlich der logistischen Funktion h(x)= 1/ (1 + ex). Diese bildet eine S-förmige Kurve.
Bei der logistischen Regression erfolgt die Ausgabe in Form von Wahrscheinlichkeiten der Standardklasse (im Gegensatz zur linearen Regression, bei der die Ausgabe direkt erfolgt). Da es sich um eine Wahrscheinlichkeit handelt, liegt die Ausgabe im Bereich von 0-1. Wenn wir also z. B. vorhersagen wollen, ob Patienten krank sind, wissen wir bereits, dass kranke Patienten mit 1 bezeichnet werden. Wenn also unser Algorithmus einem Patienten den Wert 0,98 zuweist, hält er diesen Patienten für ziemlich wahrscheinlich krank.
Diese Ausgabe (y-Wert) wird durch Log-Transformation des x-Wertes unter Verwendung der logistischen Funktion h(x)= 1/(1 + e^ -x) erzeugt. Ein Schwellenwert wird dann angewendet, um diese Wahrscheinlichkeit in eine binäre Klassifizierung zu zwingen.

Abbildung 2: Logistische Regression zur Bestimmung, ob ein Tumor bösartig oder gutartig ist. Als bösartig eingestuft, wenn die Wahrscheinlichkeit h(x)>= 0,5. Quelle
In Abbildung 2, um zu bestimmen, ob ein Tumor bösartig ist oder nicht, ist die Standardvariable y = 1 (Tumor = bösartig). Die x-Variable könnte ein Maß für den Tumor sein, z. B. die Größe des Tumors. Wie in der Abbildung dargestellt, transformiert die logistische Funktion den x-Wert der verschiedenen Instanzen des Datensatzes in den Bereich von 0 bis 1. Wenn die Wahrscheinlichkeit den Schwellenwert von 0,5 überschreitet (dargestellt durch die horizontale Linie), wird der Tumor als bösartig eingestuft.
Die logistische Regressionsgleichung P(x) = e ^ (b0 + b1x) / (1 + e(b0 + b1x)) kann in ln(p(x) / 1-p(x)) = b0 + b1x umgewandelt werden.
Das Ziel der logistischen Regression ist es, anhand der Trainingsdaten die Werte der Koeffizienten b0 und b1 so zu finden, dass der Fehler zwischen dem vorhergesagten Ergebnis und dem tatsächlichen Ergebnis minimiert wird. Diese Koeffizienten werden mit der Technik der Maximum-Likelihood-Schätzung geschätzt.
3. CART
Klassifikations- und Regressionsbäume (CART) sind eine Implementierung von Entscheidungsbäumen.
Die nicht-terminalen Knoten von Klassifikations- und Regressionsbäumen sind der Wurzelknoten und der interne Knoten. Die Endknoten sind die Blattknoten. Jeder nicht-terminale Knoten repräsentiert eine einzelne Eingangsvariable (x) und einen Aufteilungspunkt auf dieser Variable; die Blattknoten repräsentieren die Ausgangsvariable (y). Das Modell wird wie folgt verwendet, um Vorhersagen zu treffen: Gehen Sie die Splits des Baums ab, um zu einem Blattknoten zu gelangen, und geben Sie den am Blattknoten vorhandenen Wert aus.
Der Entscheidungsbaum in Abbildung 3 unten klassifiziert, ob eine Person einen Sportwagen oder einen Minivan kaufen wird, und zwar in Abhängigkeit von ihrem Alter und Familienstand. Wenn die Person über 30 Jahre alt und unverheiratet ist, gehen wir den Baum wie folgt durch: ‚über 30 Jahre?‘ -> ja -> ‚verheiratet?‘ -> nein. Folglich gibt das Modell einen Sportwagen aus.

Abbildung 3: Teile eines Entscheidungsbaums. Quelle
4. Naïve Bayes
Um die Wahrscheinlichkeit zu berechnen, dass ein Ereignis eintritt, wenn ein anderes Ereignis bereits eingetreten ist, verwenden wir das Bayes’sche Theorem. Um die Wahrscheinlichkeit zu berechnen, dass die Hypothese(h) wahr ist, wenn wir unser Vorwissen(d) haben, verwenden wir das Bayes’sche Theorem wie folgt:
wobei:
- P(h|d) = Posteriorwahrscheinlichkeit. Die Wahrscheinlichkeit, dass die Hypothese h wahr ist, wenn die Daten d gegeben sind, wobei P(h|d)= P(d1| h) P(d2| h)….P(dn| h) P(d)
- P(d|h) = Likelihood. Die Wahrscheinlichkeit der Daten d, wenn die Hypothese h wahr wäre.
- P(h) = Klassenprioritätswahrscheinlichkeit. Die Wahrscheinlichkeit, dass die Hypothese h wahr ist (unabhängig von den Daten)
- P(d) = Prädiktor-Vorauswahrscheinlichkeit. Wahrscheinlichkeit der Daten (unabhängig von der Hypothese)
Dieser Algorithmus wird „naiv“ genannt, weil er davon ausgeht, dass alle Variablen unabhängig voneinander sind, was in realen Beispielen eine naive Annahme ist.

Abbildung 4: Verwendung von Naive Bayes zur Vorhersage des Status von „Spiel“ anhand der Variable „Wetter“.
Wie lautet das Ergebnis am Beispiel von Abbildung 4, wenn Wetter = ’sonnig‘ ist?
Um das Ergebnis Spiel = ‚ja‘ oder ’nein‘ angesichts des Wertes der Variable Wetter = ’sonnig‘ zu bestimmen, berechnen Sie P(ja|sonnig) und P(nein|sonnig) und wählen Sie das Ergebnis mit der höheren Wahrscheinlichkeit.
->P(ja|sonnig)= (P(sonnig|ja) * P(ja)) / P(sunny) = (3/9 * 9/14 ) / (5/14) = 0,60
-> P(no|sunny)= (P(sunny|no) * P(no)) / P(sonnig) = (2/5 * 5/14 ) / (5/14) = 0,40
Wenn also das Wetter = „sonnig“ ist, ist das Ergebnis Spiel = „ja“.
5. KNN
Der K-Nächste-Nachbarn-Algorithmus verwendet den gesamten Datensatz als Trainingssatz, anstatt den Datensatz in einen Trainingssatz und einen Testsatz aufzuteilen.
Wenn ein Ergebnis für eine neue Dateninstanz benötigt wird, geht der KNN-Algorithmus durch den gesamten Datensatz, um die k-nächsten Instanzen zu der neuen Instanz zu finden, oder die k Anzahl von Instanzen, die dem neuen Datensatz am ähnlichsten sind, und gibt dann den Mittelwert der Ergebnisse (für ein Regressionsproblem) oder den Modus (häufigste Klasse) für ein Klassifikationsproblem aus. Der Wert von k ist benutzerspezifisch.
Die Ähnlichkeit zwischen Instanzen wird mithilfe von Maßen wie der Euklidischen Distanz und der Hamming-Distanz berechnet.
Unüberwachte Lernalgorithmen
6. Apriori
Der Apriori-Algorithmus wird in einer Transaktionsdatenbank verwendet, um häufige Elementmengen zu ermitteln und dann Assoziationsregeln zu generieren. Er wird häufig in der Warenkorbanalyse verwendet, wo man nach Kombinationen von Produkten sucht, die häufig in der Datenbank vorkommen. Im Allgemeinen schreiben wir die Assoziationsregel für „wenn eine Person Artikel X kauft, dann kauft sie auch Artikel Y“ als : X -> Y.
Beispiel: Wenn eine Person Milch und Zucker kauft, dann wird sie wahrscheinlich auch Kaffeepulver kaufen. Dies könnte in Form einer Assoziationsregel geschrieben werden als: {Milch,Zucker} -> Kaffeepulver. Assoziationsregeln werden nach Überschreiten der Schwellenwerte für Support und Konfidenz erzeugt.

Abbildung 5: Formeln für Support, Konfidenz und Lift für die Assoziationsregel X->Y.
Das Unterstützungsmaß hilft, die Anzahl der Kandidaten-Itemsets zu reduzieren, die bei der Generierung von häufigen Itemsets berücksichtigt werden. Dieses Unterstützungsmaß wird durch das Apriori-Prinzip geleitet. Das Apriori-Prinzip besagt, dass, wenn eine Itemmenge häufig ist, alle ihre Untermengen ebenfalls häufig sein müssen.
7. K-means
K-means ist ein iterativer Algorithmus, der ähnliche Daten in Clustern gruppiert.Er berechnet die Schwerpunkte von k Clustern und ordnet einen Datenpunkt demjenigen Cluster zu, der den geringsten Abstand zwischen seinem Schwerpunkt und dem Datenpunkt aufweist.

Abbildung 6: Schritte des K-means-Algorithmus. Quelle
So funktioniert es:
Zunächst wählen wir einen Wert für k. Hier sagen wir k = 3. Dann weisen wir jeden Datenpunkt zufällig einem der 3 Cluster zu. Berechnen Sie den Clusterschwerpunkt für jeden der Cluster. Die roten, blauen und grünen Sterne bezeichnen die Zentroide für jeden der 3 Cluster.
Nächste Zuweisung jedes Punktes zum nächstgelegenen Cluster-Zentroid. In der obigen Abbildung wurden die oberen 5 Punkte dem Cluster mit dem blauen Zentroid zugewiesen. Gehen Sie genauso vor, um die Punkte den Clustern mit den roten und grünen Zentroiden zuzuordnen.
Berechnen Sie dann die Zentroide für die neuen Cluster. Die alten Zentroide sind graue Sterne, die neuen Zentroide sind die roten, grünen und blauen Sterne.
Schließlich wiederholen Sie die Schritte 2 bis 3, bis es keinen Wechsel von Punkten von einem Cluster zum anderen gibt. Sobald es in zwei aufeinanderfolgenden Schritten keinen Wechsel mehr gibt, beenden Sie den K-Means-Algorithmus.
8. PCA
Die Hauptkomponentenanalyse (PCA) wird verwendet, um Daten einfach zu untersuchen und zu visualisieren, indem die Anzahl der Variablen reduziert wird. Dies geschieht durch die Erfassung der maximalen Varianz in den Daten in einem neuen Koordinatensystem mit Achsen, die „Hauptkomponenten“ genannt werden.
Jede Komponente ist eine lineare Kombination der ursprünglichen Variablen und ist orthogonal zueinander. Orthogonalität zwischen den Komponenten bedeutet, dass die Korrelation zwischen diesen Komponenten Null ist.
Die erste Hauptkomponente erfasst die Richtung der maximalen Variabilität in den Daten. Die zweite Hauptkomponente erfasst die restliche Varianz in den Daten, hat aber Variablen, die nicht mit der ersten Komponente korreliert sind. In ähnlicher Weise erfassen alle nachfolgenden Hauptkomponenten (PC3, PC4 usw.) die verbleibende Varianz, während sie mit der vorherigen Komponente unkorreliert sind.
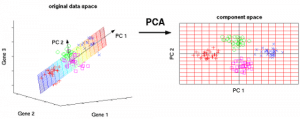
Abbildung 7: Die 3 ursprünglichen Variablen (Gene) werden auf 2 neue Variablen reduziert, die als Hauptkomponenten (PC’s) bezeichnet werden. Quelle
Ensemble-Lerntechniken:
Ensembling bedeutet, die Ergebnisse mehrerer Lerner (Klassifikatoren) zu kombinieren, um bessere Ergebnisse zu erzielen, und zwar durch Abstimmung oder Mittelwertbildung. Voting wird bei der Klassifikation und Mittelwertbildung bei der Regression verwendet. Die Idee ist, dass Ensembles von Lernern besser abschneiden als einzelne Lerner.
Es gibt 3 Arten von Ensembling-Algorithmen: Bagging, Boosting und Stacking. Wir werden hier nicht auf „Stacking“ eingehen, aber wenn Sie eine ausführliche Erklärung dazu wünschen, finden Sie hier eine solide Einführung von Kaggle.
9. Bagging mit Random Forests
Der erste Schritt beim Bagging ist die Erstellung mehrerer Modelle mit Datensätzen, die mit der Bootstrap Sampling Methode erstellt wurden. Beim Bootstrap Sampling setzt sich jeder erzeugte Trainingssatz aus zufälligen Teilproben des Originaldatensatzes zusammen.
Jeder dieser Trainingssätze hat die gleiche Größe wie der Originaldatensatz, aber einige Datensätze wiederholen sich mehrfach und einige Datensätze kommen überhaupt nicht vor. Dann wird der gesamte Originaldatensatz als Testsatz verwendet. Wenn also die Größe des Originaldatensatzes N ist, dann ist die Größe jedes generierten Trainingssatzes ebenfalls N, wobei die Anzahl der eindeutigen Datensätze etwa (2N/3) beträgt; die Größe des Testsatzes ist ebenfalls N.
Der zweite Schritt beim Bagging besteht darin, mehrere Modelle zu erstellen, indem derselbe Algorithmus auf die verschiedenen generierten Trainingssätze angewendet wird.
Hier kommen Random Forests ins Spiel. Im Gegensatz zu einem Entscheidungsbaum, bei dem jeder Knoten auf das beste Merkmal aufgeteilt wird, das den Fehler minimiert, wählen wir in Random Forests eine zufällige Auswahl von Merkmalen für die Konstruktion der besten Aufteilung. Der Grund für die Zufälligkeit ist folgender: Selbst beim Bagging, wenn Entscheidungsbäume das beste Feature zum Aufteilen wählen, enden sie mit einer ähnlichen Struktur und korrelierten Vorhersagen. Aber Bagging nach der Aufteilung auf eine zufällige Teilmenge von Merkmalen bedeutet weniger Korrelation zwischen den Vorhersagen der Teilbäume.
Die Anzahl der Merkmale, die an jedem Aufteilungspunkt gesucht werden sollen, wird als Parameter für den Random-Forest-Algorithmus angegeben.
Daher wird beim Bagging mit Random Forest jeder Baum mit einer Zufallsstichprobe von Datensätzen und jede Aufteilung mit einer Zufallsstichprobe von Prädiktoren konstruiert.
10. Boosting mit AdaBoost
Adaboost steht für Adaptive Boosting. Bagging ist ein paralleles Ensemble, da jedes Modell unabhängig aufgebaut wird. Im Gegensatz dazu ist Boosting ein sequentielles Ensemble, bei dem jedes Modell basierend auf der Korrektur der Fehlklassifikationen des vorherigen Modells erstellt wird.
Bagging beinhaltet meist eine „einfache Abstimmung“, bei der jeder Klassifikator abstimmt, um ein Endergebnis zu erhalten – eines, das von der Mehrheit der parallelen Modelle bestimmt wird; Boosting beinhaltet eine „gewichtete Abstimmung“, bei der jeder Klassifikator abstimmt, um ein Endergebnis zu erhalten, das von der Mehrheit bestimmt wird – aber die sequentiellen Modelle wurden durch die Zuweisung größerer Gewichte für falsch klassifizierte Instanzen der vorherigen Modelle erstellt.

Abbildung 9: Adaboost für einen Entscheidungsbaum. Quelle
In Abbildung 9 beinhalten die Schritte 1, 2 und 3 einen schwachen Lerner, der als Entscheidungsstumpf bezeichnet wird (ein 1-Ebenen-Entscheidungsbaum, der eine Vorhersage basierend auf dem Wert von nur einem Eingabemerkmal trifft; ein Entscheidungsbaum, dessen Wurzel unmittelbar mit seinen Blättern verbunden ist).
Der Prozess der Konstruktion von schwachen Lernern wird fortgesetzt, bis eine benutzerdefinierte Anzahl von schwachen Lernern konstruiert wurde oder bis es beim Training keine weitere Verbesserung gibt. Schritt 4 kombiniert die 3 Entscheidungsstümpfe der vorherigen Modelle (und hat somit 3 Aufteilungsregeln im Entscheidungsbaum).
Beginnen Sie mit einem Entscheidungsbaumstumpf, um eine Entscheidung über eine Eingabevariable zu treffen.
Die Größe der Datenpunkte zeigt, dass wir gleiche Gewichte angewendet haben, um sie als Kreis oder Dreieck zu klassifizieren. Der Entscheidungsstumpf hat in der oberen Hälfte eine horizontale Linie erzeugt, um diese Punkte zu klassifizieren. Es ist zu erkennen, dass es zwei Kreise gibt, die fälschlicherweise als Dreiecke vorhergesagt wurden. Daher werden wir diesen beiden Kreisen höhere Gewichte zuweisen und einen weiteren Entscheidungsbaumstumpf anwenden.
Zweitens wird ein weiterer Entscheidungsbaumstumpf verwendet, um eine Entscheidung über eine andere Eingabevariable zu treffen.
Wir stellen fest, dass die Größe der beiden falsch klassifizierten Kreise aus dem vorherigen Schritt größer ist als die der restlichen Punkte. Nun wird der zweite Entscheidungsbaumstumpf versuchen, diese beiden Kreise korrekt vorherzusagen.
Durch die Zuweisung höherer Gewichte wurden diese beiden Kreise durch die vertikale Linie auf der linken Seite korrekt klassifiziert. Dies hat nun aber dazu geführt, dass die drei Kreise oben falsch klassifiziert wurden. Daher werden wir diesen drei Kreisen oben höhere Gewichtungen zuweisen und einen weiteren Entscheidungsstumpf anwenden.
Drittes, trainieren Sie einen weiteren Entscheidungsbaumstumpf, um eine Entscheidung über eine andere Eingabevariable zu treffen.
Die drei falsch klassifizierten Kreise aus dem vorherigen Schritt sind größer als der Rest der Datenpunkte. Jetzt wurde eine vertikale Linie nach rechts erzeugt, um die Kreise und Dreiecke zu klassifizieren.
Viertens, Kombinieren der Entscheidungsstümpfe.
Wir haben die Separatoren aus den drei vorherigen Modellen kombiniert und beobachten, dass die komplexe Regel aus diesem Modell die Datenpunkte im Vergleich zu jedem der einzelnen schwachen Lerner richtig klassifiziert.
Fazit:
Zusammenfassend haben wir einige der wichtigsten maschinellen Lernalgorithmen für die Datenwissenschaft behandelt:
- 5 überwachte Lernverfahren – Lineare Regression, Logistische Regression, CART, Naïve Bayes, KNN.
- 3 unüberwachte Lerntechniken- Apriori, K-means, PCA.
- 2 Ensembling-Techniken- Bagging mit Random Forests, Boosting mit XGBoost.
Anmerkung des Herausgebers: Dieser Artikel wurde ursprünglich auf KDNuggets veröffentlicht und wurde mit Genehmigung erneut veröffentlicht. Die Autorin Reena Shaw ist Entwicklerin und Data-Science-Journalistin.

Reena Shaw ist eine Liebhaberin von allen Dingen, die mit Daten zu tun haben, von würzigem Essen und Alfred Hitchcock. Kontaktieren Sie sie über die Links in der „Weiterlesen“-Schaltfläche zu Ihrer Rechten: Linkedin| |@ReenaShawLegacy