Ein Divide-and-Conquer-Algorithmus ist eine Strategie zur Lösung eines großen Problems durch
- Zerlegung des Problems in kleinere Teilprobleme
- Lösung der Teilprobleme und
- Kombination dieser Teilprobleme, um das gewünschte Ergebnis zu erhalten.
Um den Divide-and-Conquer-Algorithmus anzuwenden, wird Rekursion verwendet. Erfahren Sie mehr über die Rekursion in verschiedenen Programmiersprachen:
- Rekursion in Java
- Rekursion in Python
- Rekursion in C++
Wie funktionieren Divide-and-Conquer-Algorithmen?
Hier sind die beteiligten Schritte:
- Teilen: Das gegebene Problem mittels Rekursion in Teilprobleme zerlegen.
- Conquer: Die kleineren Teilprobleme rekursiv lösen. Wenn das Teilproblem klein genug ist, dann lösen Sie es direkt.
- Kombinieren: Kombinieren Sie die Lösungen der Teilprobleme, die Teil des rekursiven Prozesses sind, um das eigentliche Problem zu lösen.
Lassen Sie uns dieses Konzept mit Hilfe eines Beispiels verstehen.
Hier werden wir ein Array mit dem Divide-and-Conquer-Ansatz sortieren (d.h..
- Lassen Sie das gegebene Array sein:

Array für die Mischsortierung - Teilen Sie das Array in zwei Hälften.

Teilen Sie das Array in zwei Unterteile Auch hier teilen Sie jedes Unterteil rekursiv in zwei Hälften, bis Sie einzelne Elemente erhalten.
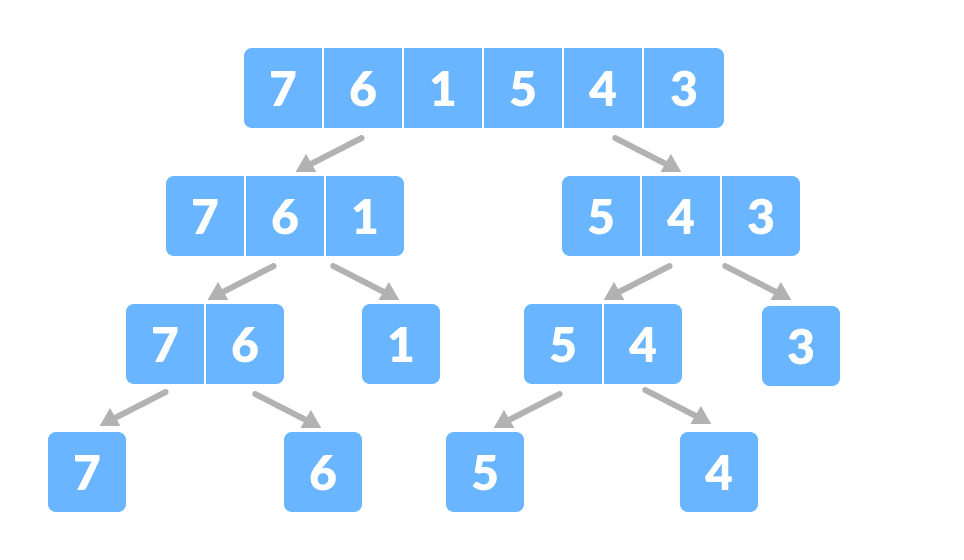
Das Array in kleinere Unterteile aufteilen - Nun kombinieren Sie die einzelnen Elemente sortiert. Hier gehen die Schritte conquer und combine Hand in Hand.
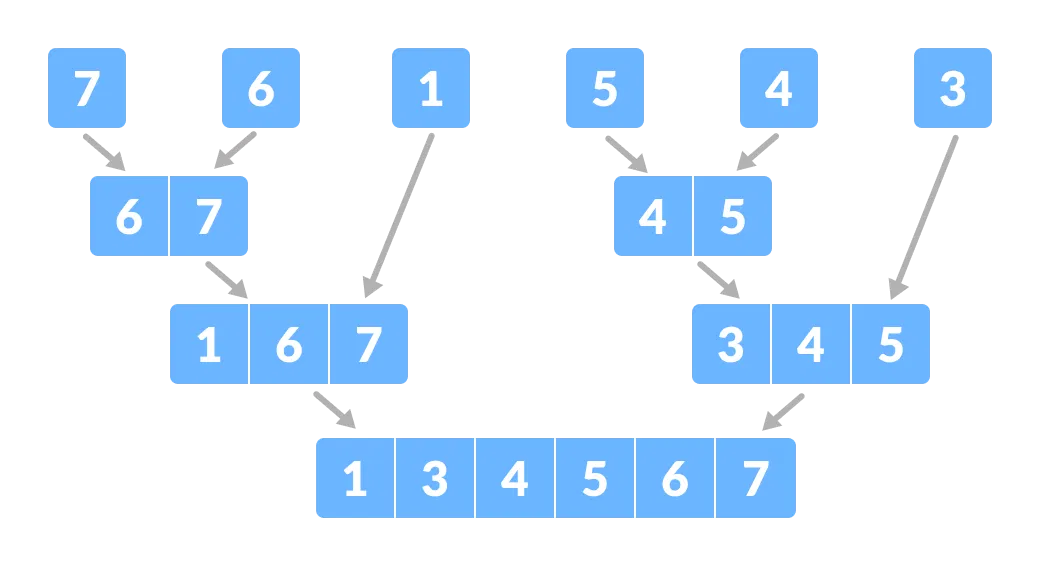
Kombinieren Sie die Unterteile
Zeitkomplexität
Die Komplexität des Divide-and-Conquer-Algorithmus wird mit Hilfe des Master-Theorems berechnet.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Lassen Sie uns ein Beispiel nehmen, um die Zeitkomplexität eines rekursiven Problems zu finden.
Für eine Merge-Sortierung kann die Gleichung geschrieben werden als:
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Divide and Conquer Vs Dynamic approach
Beim Divide and Conquer-Ansatz wird ein Problem in kleinere Teilprobleme unterteilt; diese Teilprobleme werden dann rekursiv weiter gelöst. Das Ergebnis jedes Teilproblems wird nicht für die Zukunft gespeichert, wohingegen bei einem dynamischen Ansatz das Ergebnis jedes Teilproblems für die Zukunft gespeichert wird.
Verwenden Sie den Divide-and-Conquer-Ansatz, wenn dasselbe Teilproblem nicht mehrfach gelöst wird. Verwenden Sie den dynamischen Ansatz, wenn das Ergebnis eines Teilproblems in der Zukunft mehrfach verwendet werden soll.
Lassen Sie uns dies anhand eines Beispiels verstehen. Angenommen, wir versuchen, die Fibonacci-Reihe zu finden. Dann:
Divide and Conquer Ansatz:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Dynamischer Ansatz:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
Bei einem dynamischen Ansatz wird das Ergebnis jedes Teilproblems gespeichert.
Vorteile des Divide-and-Conquer-Algorithmus
- Die Komplexität für die Multiplikation zweier Matrizen mit der naiven Methode ist O(n3), wohingegen die Verwendung des Divide-and-Conquer-Ansatzes (d. h. die Matrixmultiplikation nach Strassen) O(n2,8074) ist. Dieser Ansatz vereinfacht auch andere Probleme, wie z. B. den Turm von Hanoi.
- Dieser Ansatz ist für Multiprozessorsysteme geeignet.
- Er macht effizienten Gebrauch von Speicher-Caches.
Divide and Conquer Anwendungen
- Binäre Suche
- Merge Sort
- Quick Sort
- Strassens Matrix-Multiplikation
- Karatsuba Algorithmus



