Die Methode der Lagrange-Multiplikatoren ist das Arbeitspferd der Ökonomen zur Lösung von Optimierungsproblemen. Die Technik ist ein Kernstück der ökonomischen Theorie, aber leider wird sie meist schlecht gelehrt.
Die meisten Lehrbücher konzentrieren sich auf das mechanische Aufstellen von Formeln und lassen die Studenten im Unklaren darüber, warum sie eigentlich funktioniert. In diesem Beitrag erkläre ich einen einfachen Weg, um zu sehen, warum Lagrange-Multiplikatoren tatsächlich das tun, was sie tun – nämlich eingeschränkte Optimierungsprobleme durch die Verwendung einer halbmysteriösen Lagrange-Funktion lösen.
Ein wenig Hintergrund
Bevor Sie sehen können, warum die Methode funktioniert, müssen Sie etwas über Gradienten wissen. Für Funktionen von einer Variablen gibt es – normalerweise – eine erste Ableitung. Für Funktionen von n Variablen gibt es n erste Ableitungen. Ein Gradient ist einfach ein Vektor, der alle partiellen ersten Ableitungen der Funktion an einem Ort sammelt.
Jedes Element im Gradienten ist eine der partiellen ersten Ableitungen der Funktion. Eine einfache Art, sich einen Gradienten vorzustellen, ist, dass er uns die „Richtung“ der Funktion angibt, wenn wir einen Punkt auf einer Funktion auswählen. Wenn unsere Funktion beschriftet ist
die Notation für die Steigung von f lautet
Das Wichtigste, was man über Steigungen wissen muss, ist, dass sie immer in die Richtung der steilsten Steigung einer Funktion an einem bestimmten Punkt zeigen. Um dies zu verdeutlichen, sehen Sie sich die folgende Zeichnung an. Sie veranschaulicht, wie Gradienten für eine Funktion mit zwei Variablen aus x1 und x2 funktionieren.
Die Funktion f in der Zeichnung bildet einen Hügel. Zur Spitze hin habe ich zwei Bereiche eingezeichnet, in denen wir die Höhe von f auf einem bestimmten Niveau a konstant halten. Diese werden als Niveaukurven von f bezeichnet und sind mit f = a1 und f = a2 markiert.
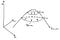
Stellen Sie sich vor, Sie stehen auf einer dieser ebenen Kurven. Denken Sie an einen Wanderweg an einem Berghang. Wenn Sie auf dem Pfad stehen, in welche Richtung ist der Berg am steilsten? Offensichtlich ist die steilste Richtung gerade den Berg hinauf, senkrecht zum Wanderweg. In der Zeichnung sind diese Wege des steilsten Anstiegs mit Pfeilen markiert. Dies sind die Steigungen
an verschiedenen Stellen entlang der Höhenkurven. So wie die steilste Wanderung immer senkrecht auf unserem Weg steht, stehen die Steigungen von f immer senkrecht auf den ebenen Kurven.
Das ist die Schlüsselidee hier: Ebenenkurven sind dort, wo
und
Wie die Methode funktioniert
Um zu sehen, wie Lagrange-Multiplikatoren funktionieren, werfen Sie einen Blick auf die folgende Zeichnung. Ich habe die Funktion f von oben neu gezeichnet, zusammen mit einer Zwangsbedingung g = c. In der Zeichnung ist die Zwangsbedingung eine Ebene, die durch unseren Hang schneidet. Ich habe auch ein paar Ebenen-Kurven von f gezeichnet.

Unser Ziel ist es, so hoch auf den Hügel zu klettern, wie wir können, vorausgesetzt, wir können nicht höher klettern als dort, wo die Bedingung g = c den Hügel schneidet.
In der Zeichnung ist die Grenze, an der die Zwangsbedingung die Funktion schneidet, mit einer dicken Linie markiert. Entlang dieser Linie liegen die höchsten Punkte, die wir erreichen können, ohne unsere Zwangsbedingung zu überschreiten. Das ist ein offensichtlicher Ort, um mit der Suche nach einem gebundenen Maximum zu beginnen.
Stellen Sie sich vor, Sie wandern von links nach rechts auf der Bindungslinie. Während wir an Höhe gewinnen, gehen wir durch verschiedene Niveaukurven von f. Ich habe zwei im Bild markiert. Stellen Sie sich vor, dass Sie an jeder ebenen Kurve die Steigung überprüfen – also die Steigung einer Tangente an die Kurve – und diese mit der Steigung auf der Zwangsbedingung vergleichen, auf der wir gerade stehen.
Wenn unsere Steigung größer ist als die ebene Kurve, können wir einen höheren Punkt auf dem Hügel erreichen, wenn wir weiter nach rechts gehen. Wenn unsere Steigung kleiner ist als die Niveaulinie – z. B. nach rechts, wo unsere Constraint-Linie abfällt – müssen wir uns nach links zurückbewegen, um einen höheren Punkt zu erreichen.
Wenn wir einen Punkt erreichen, an dem die Steigung der Constraint-Linie gerade der Steigung der Niveaulinie entspricht, haben wir uns so hoch wie möglich bewegt. Das heißt, wir haben unser gebundenes Maximum erreicht. Jede weitere Bewegung von diesem Punkt aus führt uns nach unten. In der Abbildung ist dieser Punkt mit einem großen Pfeil markiert, der auf die Spitze zeigt.
An diesem Punkt haben die Pegelkurve f = a2 und die Zwangsbedingung die gleiche Steigung. Das heißt, sie sind parallel und zeigen in dieselbe Richtung. Aber wie wir oben gesehen haben, sind Steigungen immer senkrecht zu Niveaukurven. Wenn also diese beiden Kurven parallel sind, müssen auch ihre Steigungen parallel sein.
Das bedeutet, dass die Steigungen von f und g beide in dieselbe Richtung zeigen und sich höchstens um einen Skalar unterscheiden. Nennen wir diesen Skalar „lambda“. Dann haben wir,
Auflösen für Null, erhalten wir
Dies ist die Bedingung, die gelten muss, wenn wir das Maximum von f unter der Nebenbedingung g = c erreicht haben. Wenn wir clever sind, können wir eine einzige Gleichung schreiben, die diese Idee einfängt. Hier kommt die bekannte Lagrangesche Gleichung ins Spiel:
oder noch expliziter,
Um zu sehen, wie diese Gleichung funktioniert, schauen wir uns an, was passiert, wenn wir dem üblichen Lagrangeschen Verfahren folgen. Zuerst finden wir die drei partiellen ersten Ableitungen von L,
und setzen sie gleich Null. Das heißt, wir müssen die Steigung von L gleich Null setzen. Um die Steigung von L zu finden, nehmen wir die drei partiellen Ableitungen von L in Bezug auf x1, x2 und lambda. Dann setzen wir jede als ein Element in einen 3 x 1 Vektor. So erhalten wir Folgendes:
Erinnern Sie sich, dass wir hier zwei „Regeln“ zu befolgen haben. Erstens, die Steigungen von f und g müssen in die gleiche Richtung zeigen, oder
Und zweitens müssen wir unsere Bedingung erfüllen, oder
Das erste und zweite Element des Gradienten von L sorgen dafür, dass die erste Regel eingehalten wird. D.h., sie erzwingen
Damit ist sichergestellt, dass die Steigungen von f und g beide in dieselbe Richtung zeigen. Das dritte Element des Gradienten von L ist einfach ein Trick, um sicherzustellen, dass g = c ist, was unsere Nebenbedingung ist. Wenn wir in der Lagrange-Funktion die partielle Ableitung nach Lambda nehmen, erhalten wir einfach unsere ursprüngliche Zwangsbedingungsgleichung zurück.
An dieser Stelle haben wir drei Gleichungen mit drei Unbekannten. Wir können sie also für die optimalen Werte von x1 und x2 lösen, die f unter Berücksichtigung unserer Nebenbedingung maximieren. Und wir sind fertig.
Unterm Strich ist der Lagrange-Multiplikator also nur ein Algorithmus, der herausfindet, wo der Gradient einer Funktion in die gleiche Richtung wie die Gradienten ihrer Nebenbedingungen zeigt, während er gleichzeitig diese Nebenbedingungen erfüllt.
Wie in den meisten Bereichen der Mathematik sind die Dinge viel einfacher, als die meisten Ökonomen sie darstellen, wenn man den Dingen erst einmal auf den Grund gegangen ist – in diesem Fall, dass Optimierung eigentlich nur Hillclimbing ist, was jeder versteht.