Zurück zum Lektionsindex | Lektionen der Reihe nach bearbeiten | Druckfreundliche Seite
Faktoren
Faktoren sind sehr einfache Dinge. Sie sind einfach Produkte, die durch ein Ausrufezeichen gekennzeichnet sind. Zum Beispiel wird „vierfaktoriell“ als „4!“ geschrieben und bedeutet 1×2×3×4 = 24. Im Allgemeinen wird n! („enn faktoriell“) bedeutet das Produkt aller ganzen Zahlen von 1 bis n, also n! = 1×2×3×…×n.
(Aus verschiedenen Gründen ist 0! als gleich 1 definiert, nicht als 0. Prägen Sie sich das gut ein: 0! = 1.)
- Werten Sie 6! aus.
1×2×3×4×5×6 = 720
Viele (die meisten?) Taschenrechner können Faktorzahlen für Sie auswerten. Auf einem meiner Taschenrechner ist der Befehl für die Fakultät zum Beispiel im Menü „Wahrscheinlichkeit“ verfügbar:

Suchen Sie nach einer “ ! “ Taste, oder schauen Sie in der Bedienungsanleitung nach.
- Vereinfachen Sie 12! Copyright © Elizabeth Stapel 2004-2011 Alle Rechte vorbehalten
12! = 1×2×3×4×… Ach, was soll’s. Wo ist mein Taschenrechner…?

12! = 479001600
Anmerkung
Wenn Sie anfangen, sich mit Kombinationen, Permutationen und Wahrscheinlichkeiten zu beschäftigen, werden Sie Ausdrücke vereinfachen, die Faktoren im Zähler und im Nenner haben. Zum Beispiel:
- Vereinfachen Sie Folgendes:
![]()
Ich kann das in meinem Taschenrechner machen:

Ich kann auch mit der Definition einer Fakultät arbeiten:
![]()
In beiden Fällen gilt: 6! ÷ 4! = 30
Beachten Sie, wie ich in der vorherigen Aufgabe eine Reihe von Zahlen streichen konnte. Das liegt daran, wie Faktoren definiert sind, und diese Eigenschaft kann Ihre Arbeit sehr vereinfachen.
- Vereinfachen Sie Folgendes:
![]()
Sofort kann ich die Faktoren 1 bis 14 streichen, die sowohl 17! als auch 14! gemeinsam sind. Dann kann ich vereinfachen, was übrig bleibt und erhalte:
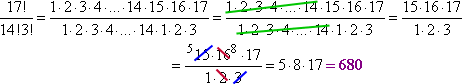
Beachten Sie, wie ich das, was ich schreiben musste, verkürzt habe, indem ich in der Mitte eine Lücke (die „Ellipse“ oder den Dreifach-Periodenstrich) ließ. Dieses Lücken- und Abbruchverfahren wird später sehr nützlich sein (z. B. in der Analysis, wo Sie diese Technik oft verwenden werden), besonders wenn Sie mit Ausdrücken zu tun haben, die Ihr Taschenrechner nicht verarbeiten kann. Zum Beispiel:
- Vereinfachen Sie das Folgende:
![]()
Mein Taschenrechner kann das nicht für mich auswerten, da ich es mit Variablen und nicht mit Zahlen zu tun habe. Ich muss das von Hand vereinfachen. Dazu werde ich die Faktoren ausschreiben und dabei so viele Faktoren verwenden, dass sich die Dinge aufheben können. Wenn ich an „Zahlen“-Wortprobleme zurückdenke, sind aufeinanderfolgende ganze Zahlen eine Einheit voneinander entfernt, also haben die Faktoren im Produkt (n + 2)! die Form:
1×2×3×4×…×(n – 1)×(n)×(n + 1)×(n + 2)
Indem ich die Liste der Faktoren bis zu „n – 1“ zurückverfolge, habe ich eine Liste von Faktoren erstellt, die sich aufheben können:
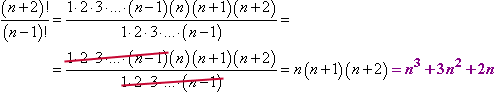
Beachten Sie die Art und Weise, wie ich diese Aufhebung behandelt habe. Ich habe die faktoriellen Ausdrücke so erweitert, dass ich sehen konnte, wo ich doppelte Faktoren streichen kann. Auch wenn ich keine Ahnung hatte, wie groß n sein könnte, konnte ich trotzdem stornieren. Merken Sie sich diese Technik, denn auch wenn Sie sie jetzt nicht brauchen, werden Sie sie später mit Sicherheit brauchen.
Für Informationen über die Anzahl der Nullen am Ende einer Fakultät (z. B. „Wie viele Nullen stehen am Ende von 23! nachdem man sie ausmultipliziert hat?“), schauen Sie sich diesen Hinweis an.
Top | Zurück zum Index
|
Zitiere diesen Artikel als: |
Stapel, Elizabeth. „Factorials.“ Purplemath. Verfügbar unter 2016
|