⇐ Vorheriges Thema|Nächstes Thema ⇒ Inhaltsverzeichnis
Bevor Sie ein Experiment durchführen, sollten Sie eine Power-Analyse durchführen, um die Anzahl der Beobachtungen abzuschätzen, die Sie benötigen, um eine gute Chance zu haben, den gesuchten Effekt zu entdecken.
Einleitung
Wenn Sie ein Experiment planen, ist es eine gute Idee, die benötigte Stichprobengröße abzuschätzen. Das gilt besonders dann, wenn Sie vorhaben, etwas Schmerzhaftes an Menschen oder anderen Wirbeltieren durchzuführen, wo es besonders wichtig ist, die Anzahl der Individuen zu minimieren (ohne die Stichprobengröße so klein zu machen, dass das ganze Experiment eine Verschwendung von Zeit und Leid ist), oder wenn Sie ein sehr zeitaufwendiges oder teures Experiment planen. Für viele statistische Tests wurden Methoden entwickelt, um die Stichprobengröße zu schätzen, die benötigt wird, um einen bestimmten Effekt zu entdecken, oder um die Größe des Effekts zu schätzen, der mit einer bestimmten Stichprobengröße entdeckt werden kann.
Um eine Power-Analyse durchzuführen, müssen Sie eine Effektgröße angeben. Dies ist die Größe des Unterschieds zwischen Ihrer Nullhypothese und der Alternativhypothese, die Sie zu entdecken hoffen. In der angewandten und klinischen biologischen Forschung kann es eine ganz bestimmte Effektgröße geben, die Sie nachweisen möchten. Wenn Sie z. B. ein neues Hundeshampoo testen, könnte die Marketingabteilung Ihrer Firma Ihnen sagen, dass sich die Herstellung des neuen Shampoos nur dann lohnt, wenn es das Fell der Hunde im Durchschnitt um mindestens 25 % glänzender macht. Das wäre Ihre Effektgröße, und Sie würden sie verwenden, wenn Sie entscheiden, wie viele Hunde Sie durch das Hundereflektometer schicken müssen.
Bei biologischer Grundlagenforschung weiß man oft nicht, wie groß der Unterschied ist, nach dem man sucht, und die Versuchung kann darin bestehen, einfach die größte Stichprobengröße zu verwenden, die man sich leisten kann, oder eine ähnliche Stichprobengröße wie bei anderen Untersuchungen in Ihrem Bereich zu verwenden. Sie sollten dennoch eine Power-Analyse durchführen, bevor Sie das Experiment durchführen, nur um eine Vorstellung davon zu bekommen, welche Art von Effekten Sie entdecken könnten. Zum Beispiel haben einige Impfgegner vorgeschlagen, dass die US-Regierung eine große Studie mit ungeimpften und geimpften Kindern durchführt, um zu sehen, ob Impfstoffe Autismus verursachen. Es ist nicht klar, welche Effektgröße interessant wäre: 10% mehr Autismus in einer Gruppe? 50% mehr? doppelt so viel? Eine Power-Analyse zeigt jedoch, dass selbst wenn die Studie jedes ungeimpfte Kind in den USA im Alter von 3 bis 6 Jahren und eine gleiche Anzahl von geimpften Kindern einschließen würde, es 25% mehr Autismus in einer Gruppe geben müsste, um eine hohe Chance zu haben, einen signifikanten Unterschied zu sehen. Eine plausiblere Studie mit 5.000 ungeimpften und 5.000 geimpften Kindern würde nur dann einen signifikanten Unterschied mit hoher Aussagekraft feststellen, wenn es in einer Gruppe dreimal mehr Autismus gäbe als in der anderen. Da es unwahrscheinlich ist, dass es einen so großen Unterschied zwischen geimpften und ungeimpften Kindern in Bezug auf Autismus gibt, und da das Nichtfinden eines Zusammenhangs mit einer solchen Studie die Impfgegner nicht davon überzeugen würde, dass es keinen Zusammenhang gibt (nichts würde sie davon überzeugen, dass es keinen Zusammenhang gibt – das ist es, was sie zu Spinnern macht), sagt Ihnen die Power-Analyse, dass sich eine so große, teure Studie nicht lohnen würde.
Parameter
Es gibt vier oder fünf Zahlen, die an einer Power-Analyse beteiligt sind. Sie müssen die Werte für jede einzelne davon auswählen, bevor Sie die Analyse durchführen. Wenn Sie keinen guten Grund für die Verwendung eines bestimmten Wertes haben, können Sie verschiedene Werte ausprobieren und die Auswirkung auf die Stichprobengröße betrachten.
Effektgröße
Die Effektgröße ist die minimale Abweichung von der Nullhypothese, die Sie zu entdecken hoffen. Wenn Sie zum Beispiel Hühner mit etwas behandeln, von dem Sie hoffen, dass es das Geschlechterverhältnis ihrer Küken verändert, könnten Sie entscheiden, dass die minimale Veränderung im Geschlechterverhältnis, nach der Sie suchen, 10 % beträgt. Sie würden dann sagen, dass Ihre Effektgröße 10 % beträgt. Wenn Sie etwas testen, das die Hühner dazu bringt, mehr Eier zu legen, könnte die Effektgröße 2 Eier pro Monat sein.
Gelegentlich haben Sie einen guten ökonomischen oder klinischen Grund für die Wahl einer bestimmten Effektgröße. Wenn Sie ein Hühnerfuttermittel testen, das 1,50 $ pro Monat kostet, sind Sie nur daran interessiert, herauszufinden, ob es mehr als 1,50 $ an zusätzlichen Eiern pro Monat produziert; zu wissen, dass ein Mittel 0,1 zusätzliche Eier pro Monat produziert, ist keine nützliche Information für Sie, und Sie müssen Ihr Experiment nicht so anlegen, dass Sie das herausfinden. Aber für die meisten grundlegenden biologischen Untersuchungen ist die Effektgröße nur eine nette runde Zahl, die Sie sich aus dem Hintern gezogen haben. Nehmen wir an, Sie machen eine Power-Analyse für eine Studie über eine Mutation in einer Promotorregion, um zu sehen, ob sie die Genexpression beeinflusst. Nach wie viel Veränderung in der Genexpression suchen Sie? 10%? 20%? 50%? Das ist eine ziemlich willkürliche Zahl, aber sie wird einen großen Einfluss auf die Anzahl der transgenen Mäuse haben, die ihr teures kleines Leben für Ihre Wissenschaft geben werden. Wenn Sie keinen guten Grund haben, nach einer bestimmten Effektgröße zu suchen, können Sie das genauso gut zugeben und ein Diagramm mit der Stichprobengröße auf der X-Achse und der Effektgröße auf der Y-Achse zeichnen. G*Power erledigt das für Sie.
Alpha
Alpha ist das Signifikanzniveau des Tests (der P-Wert), die Wahrscheinlichkeit, die Nullhypothese zurückzuweisen, obwohl sie wahr ist (ein falsches Positiv). Der übliche Wert ist alpha=0,05. Einige Potenzrechner verwenden das einseitige Alpha, was verwirrend ist, da das zweiseitige Alpha viel üblicher ist. Stellen Sie sicher, dass Sie wissen, welchen Wert Sie verwenden.
Beta oder Power
Beta ist in einer Power-Analyse die Wahrscheinlichkeit, die Nullhypothese anzunehmen, obwohl sie falsch ist (ein falsches Negativ), wenn der tatsächliche Unterschied gleich der minimalen Effektgröße ist. Die Potenz eines Tests ist die Wahrscheinlichkeit, die Nullhypothese abzulehnen (ein signifikantes Ergebnis zu erhalten), wenn der tatsächliche Unterschied gleich der Mindesteffektgröße ist. Die Potenz ist 1-beta. Es gibt keinen klaren Konsens über den zu verwendenden Wert, also ist dies eine weitere Zahl, die Sie aus dem Ärmel schütteln; eine Potenz von 80 % (entspricht einem Beta von 20 %) ist wahrscheinlich die gebräuchlichste, während einige Leute 50 % oder 90 % verwenden. Die Kosten, die Ihnen ein falsches Negativ verursacht, sollten Ihre Wahl der Power beeinflussen; wenn Sie wirklich sicher sein wollen, dass Sie Ihre Effektgröße entdecken, werden Sie einen höheren Wert für die Power (niedrigeres Beta) verwenden wollen, was zu einem größeren Stichprobenumfang führt. Einige Potenzrechner fordern Sie auf, Beta einzugeben, während andere nach der Potenz (1-Beta) fragen; seien Sie sehr sicher, dass Sie verstehen, welche Sie verwenden müssen.
Standardabweichung
Für Messvariablen benötigen Sie auch eine Schätzung der Standardabweichung. Je größer die Standardabweichung ist, desto schwieriger wird es, einen signifikanten Unterschied festzustellen, sodass Sie eine größere Stichprobengröße benötigen. Ihre Schätzung der Standardabweichung kann aus Pilotexperimenten oder aus ähnlichen Experimenten aus der veröffentlichten Literatur stammen. Es ist unwahrscheinlich, dass Ihre Standardabweichung nach der Durchführung des Experiments genau gleich ist, so dass Ihr Experiment tatsächlich etwas mehr oder weniger aussagekräftig sein wird, als Sie vorhergesagt haben.
Für nominale Variablen ist die Standardabweichung eine einfache Funktion des Stichprobenumfangs, so dass Sie sie nicht separat schätzen müssen.
Wie es funktioniert
Die Details einer Power-Analyse sind für verschiedene statistische Tests unterschiedlich, aber die grundlegenden Konzepte sind ähnlich; hier werde ich den exakten Binomialtest als Beispiel verwenden. Stellen Sie sich vor, Sie untersuchen Handgelenksfrakturen und Ihre Nullhypothese ist, dass die Hälfte der Menschen, die sich ein Handgelenk brechen, sich das rechte Handgelenk brechen, und die Hälfte das linke. Sie entscheiden, dass die minimale Effektgröße 10 % beträgt; wenn der Prozentsatz der Personen, die sich das rechte Handgelenk brechen, 60 % oder mehr oder 40 % oder weniger beträgt, wollen Sie ein signifikantes Ergebnis aus dem exakten Binomialtest haben. Ich habe keine Ahnung, warum Sie 10% gewählt haben, aber das ist es, was Sie verwenden werden. Alpha ist 5%, wie üblich. Sie wollen eine Potenz von 90%, d.h. wenn der Prozentsatz der gebrochenen rechten Handgelenke wirklich 40% oder 60% beträgt, wollen Sie eine Stichprobengröße, die in 90% der Fälle ein signifikantes (P<0,05) Ergebnis liefert, und in nur 10% der Fälle ein nicht signifikantes Ergebnis (was in diesem Fall ein falsches Negativ wäre).
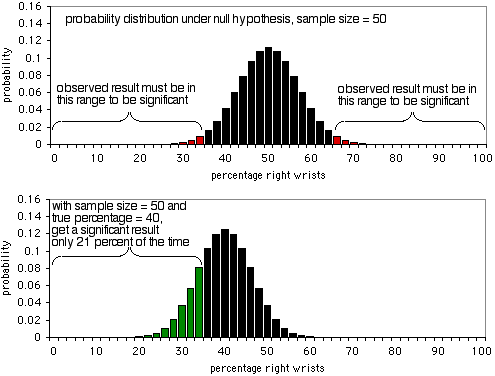

Der erste Graph zeigt die Wahrscheinlichkeitsverteilung unter der Nullhypothese, mit einer Stichprobengröße von 50 Individuen. Wenn die Nullhypothese wahr ist, werden etwa 5 % der Personen weniger als 36 % oder mehr als 64 % der Personen ihr rechtes Handgelenk brechen (ein falsches Positiv). Wie das zweite Diagramm zeigt, sind die Stichprobendaten bei einem wahren Prozentsatz von 40 % nur in 21 % der Fälle kleiner als 36 oder größer als 64 %; Sie würden also nur in 21 % der Fälle ein wahres Positiv und in 79 % der Fälle ein falsches Negativ erhalten. Offensichtlich ist eine Stichprobengröße von 50 zu klein für dieses Experiment; es würde nur in 21% der Fälle ein signifikantes Ergebnis liefern, selbst wenn es ein 40:60-Verhältnis von gebrochenen rechten Handgelenken zu linken Handgelenken gibt.
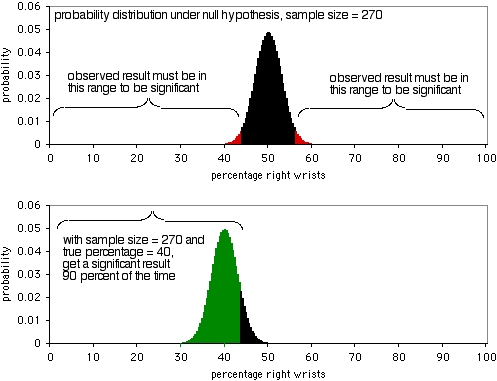

Der nächste Graph zeigt die Wahrscheinlichkeitsverteilung unter der Nullhypothese, mit einer Stichprobengröße von 270 Individuen. Um auf dem P<0,05-Niveau signifikant zu sein, müsste das beobachtete Ergebnis weniger als 43,7% oder mehr als 56,3% der Personen betragen, die sich das rechte Handgelenk brechen. Wie das zweite Diagramm zeigt, wenn der wahre Prozentsatz 40% beträgt, werden die Stichprobendaten in 90% der Fälle dieses Extrem aufweisen. Eine Stichprobengröße von 270 ist ziemlich gut für dieses Experiment; es würde in 90% der Fälle ein signifikantes Ergebnis liefern, wenn das Verhältnis von gebrochenen rechten Handgelenken zu linken Handgelenken 40:60 ist. Wenn das Verhältnis von gebrochenen rechten zu linken Handgelenken weiter von 50:50 entfernt ist, haben Sie eine noch höhere Wahrscheinlichkeit, ein signifikantes Ergebnis zu erhalten.
Beispiele
Sie planen, Erbsen zu kreuzen, die heterozygot für die Erbsenfarbe Gelb/Grün sind, wobei Gelb dominant ist. Das erwartete Verhältnis in der Nachkommenschaft ist 3 Gelb: 1 Grün. Sie möchten wissen, ob gelbe Erbsen tatsächlich mehr oder weniger fit sind, was sich als ein anderer Anteil an gelben Erbsen als erwartet zeigen könnte. Sie entscheiden willkürlich, dass Sie eine Stichprobengröße wollen, die einen signifikanten (P<0,05) Unterschied entdeckt, wenn es 3% mehr oder weniger gelbe Erbsen als erwartet gibt, mit einer Potenz von 90%. Sie testen die Daten mit dem exakten Binomialtest der Anpassungsgüte, wenn der Stichprobenumfang klein genug ist, oder mit einem G-Test der Anpassungsgüte, wenn der Stichprobenumfang größer ist. Die Potenzanalyse ist für beide Tests gleich.
Bei Verwendung von G*Power, wie für den exakten Test der Anpassungsgüte beschrieben, ergibt sich, dass man 2109 Erbsenpflanzen benötigen würde, um in 90% der Fälle ein signifikantes (P<0,05) Ergebnis zu erhalten, wenn der wahre Anteil der gelben Erbsen 78% beträgt, und 2271 Erbsen, wenn der wahre Anteil 72% gelb ist. Da Sie an einer Abweichung in beide Richtungen interessiert wären, verwenden Sie die größere Zahl, 2271. Das ist eine Menge Erbsen, aber Sie können beruhigt sein, dass es keine lächerliche Zahl ist. Wenn Sie einen Unterschied von 0,1 % zwischen der erwarteten und der beobachteten Anzahl gelber Erbsen feststellen wollen, können Sie berechnen, dass Sie 1.970.142 Erbsen benötigen; wenn das das ist, was Sie feststellen müssen, sagt Ihnen die Stichprobengrößenanalyse, dass Sie einen Erbsensortierroboter in Ihr Budget aufnehmen müssen.
Die Beispieldaten für den t-Test mit zwei Stichproben zeigen, dass die durchschnittliche Körpergröße im Abschnitt „Biologische Datenanalyse“ um 14 Uhr 66,6 cm und im Abschnitt „Biologische Datenanalyse“ um 17 Uhr 64,6 cm betrug, aber der Unterschied ist nicht signifikant (P=0,207). Sie möchten wissen, wie viele Schüler Sie in die Stichprobe aufnehmen müssten, um eine 80%ige Chance zu haben, dass ein so großer Unterschied signifikant ist. Geben Sie unter Verwendung von G*Power, wie auf der Seite t-Test für zwei Stichproben beschrieben, 2,0 für die Differenz der Mittelwerte ein. Berechnen Sie mithilfe der Funktion STDEV in Excel die Standardabweichung für jede Stichprobe in den Originaldaten; sie beträgt 4,8 für Stichprobe 1 und 3,6 für Stichprobe 2. Geben Sie 0,05 für Alpha und 0,80 für Power ein. Das Ergebnis ist 72, was bedeutet, dass Sie, wenn die Schüler um 17 Uhr wirklich zwei Zentimeter kleiner sind als die Schüler um 14 Uhr, 72 Schüler in jeder Klasse benötigen, um in 80 % der Fälle einen signifikanten Unterschied zu erkennen, wenn der wahre Unterschied wirklich 2,0 Zentimeter beträgt.
Wie man Power-Analysen durchführt
G*Power
G*Power ist ein ausgezeichnetes, kostenloses Programm, das für Mac und Windows verfügbar ist und Power-Analysen für eine große Anzahl von Tests durchführt. Ich werde erklären, wie man G*Power für Power-Analysen für die meisten Tests in diesem Handbuch verwendet.
R
Salvatore Mangiafico’s R Companion hat R-Beispielprogramme, um Power-Analysen für viele der Tests in diesem Handbuch durchzuführen; gehen Sie auf die Seite für den individuellen Test und scrollen Sie nach unten, um das Power-Analyseprogramm zu finden.
SAS
SAS hat ein PROC POWER, das Sie für Power-Analysen verwenden können. Sie geben die benötigten Parameter ein (die je nach Test variieren) und geben einen Punkt (der in SAS fehlende Daten symbolisiert) für den Parameter ein, für den Sie eine Lösung suchen (normalerweise ntotal, die gesamte Stichprobengröße, oder npergroup, die Anzahl der Stichproben in jeder Gruppe). Ich finde, dass G*Power für diesen Zweck einfacher zu verwenden ist als SAS, daher empfehle ich nicht, SAS für Ihre Power-Analysen zu verwenden.
⇐ Vorheriges Thema|Nächstes Thema ⇒ Inhaltsverzeichnis
Diese Seite wurde zuletzt am 20. Juli 2015 überarbeitet. Sie trägt die Adresse http://www.biostathandbook.com/power.html. Sie kann zitiert werden als:
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. Diese Webseite enthält den Inhalt der Seiten 40-44 in der gedruckten Version.
©2014 by John H. McDonald. Sie können mit diesem Inhalt wahrscheinlich machen, was Sie wollen; siehe die Seite mit den Genehmigungen für Details.