Heading

Was ist ein Interquartilsbereich?

Der Interquartilsbereich ist ein Maß dafür, wo die „Mitte fünfzig“ in einem Datensatz ist. Während ein Bereich ein Maß dafür ist, wo der Anfang und das Ende in einer Menge liegen, ist ein Interquartilsbereich ein Maß dafür, wo der Großteil der Werte liegt. Deshalb wird er gegenüber vielen anderen Streuungsmaßen bevorzugt, wenn Dinge wie Schulleistungen oder SAT-Scores berichtet werden.

Die Formel für den Interquartilsbereich ist das erste Quartil subtrahiert vom dritten Quartil:

Inhalt (Klicken Sie, um zum Seitenabschnitt zu springen):

Lösen Sie die Formel von Hand:

1. Lösen Sie die Formel von Hand (ungerade Zahlenmenge).
2. Was ist, wenn ich eine gerade Zahlenmenge habe?
3. Ermitteln Sie einen Interquartilsbereich für eine ungerade Zahlenmenge: Zweite Methode
4. Box Plot Interquartilsbereich: Wie man ihn findet

Mit Hilfe der Technik:

1. Interquartilsbereich in Minitab
2. Interquartilsbereich in Excel
3. Interquartilsbereich in SPSS
4. Interquartilsbereich auf dem TI83
5. Q1, Q3 und der IQR auf dem TI89

Allgemeine Informationen:

1. Was ist ein Interquartilsbereich?
2. Was ist die Interquartilsbereichsformel?
3. IQR als Test für die Normalverteilung
4. Wofür wird ein Interquartilsbereich verwendet?
5. Geschichte des Interquartilsbereichs.

Lösen Sie die Formel von Hand.

Schauen Sie sich das Video an oder lesen Sie die Schritte unten. Wenn Sie immer noch Schwierigkeiten haben, schauen Sie sich die Tutoren auf Chegg.com an. Die ersten 30 Minuten sind kostenlos!

Schritte:

• Schritt 1: Bringen Sie die Zahlen in die richtige Reihenfolge.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
• Schritt 2: Finde den Median.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
• Schritt 3: Setze Klammern um die Zahlen oberhalb und unterhalb des Medians.
  Statistisch nicht notwendig, aber es macht Q1 und Q3 leichter zu erkennen.
  (1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27).
• Schritt 4: Finden Sie Q1 und Q3
  Betrachten Sie Q1 als Median in der unteren Hälfte der Daten und betrachten Sie Q3 als Median für die obere Hälfte der Daten.
  (1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27). Q1 = 5 und Q3 = 18.
• Schritt 5: Subtrahieren Sie Q1 von Q3, um den Interquartilsbereich zu finden.
  18 – 5 = 13.

Like the explanation? Schauen Sie sich das Handbuch Praktisch schummelnder Statistik an, das Hunderte weiterer Schritt-für-Schritt-Erklärungen enthält, genau wie diese!

Was ist, wenn ich eine gerade Menge von Zahlen habe?

Beispielfrage: Finden Sie den IQR für den folgenden Datensatz: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.

• Schritt 1: Bringen Sie die Zahlen in die richtige Reihenfolge.
  3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
• Schritt 2: Machen Sie eine Markierung in der Mitte der Daten:
  3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
• Schritt 3: Setzen Sie Klammern um die Zahlen über und unter der Markierung, die Sie in Schritt 2 gemacht haben – so sind Q1 und Q3 leichter zu erkennen.
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).
• Schritt 4: Finden Sie Q1 und Q3
  Q1 ist der Median (die Mitte) der unteren Hälfte der Daten, und Q3 ist der Median (die Mitte) der oberen Hälfte der Daten.
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 und Q3 = 16.
• Schritt 5: Subtrahieren Sie Q1 von Q3.
  16 – 7 = 9.
  Das ist Ihr IQR.

Zurück zum Anfang

Bestimmen Sie einen Interquartilsbereich für eine ungerade Menge von Zahlen: Alternative Methode

Wie Sie vielleicht schon wissen, ist in der Statistik nichts „in Stein gemeißelt“: Wenn einige Statistiker einen Interquartilsbereich für eine Menge ungerader Zahlen finden, schließen sie den Median in beide Quartile ein. Zum Beispiel in der folgenden Zahlenreihe: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 würden einige Statistiker sie in zwei Hälften aufteilen und den Median (9) in beide Hälften einschließen:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Das führt zu zwei Hälften mit einem geraden Satz von Zahlen, so dass Sie die obigen Schritte befolgen können, um den IQR zu finden.
Zurück zum Anfang

Box Plot Interquartilsbereich: Wie man ihn findet

Schauen Sie sich das Video an oder lesen Sie die Schritte unten:

Box Plot Interquartilsbereich: Wie man ihn findet

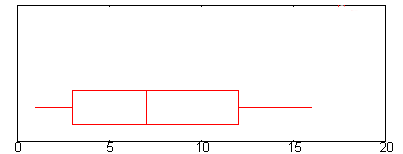
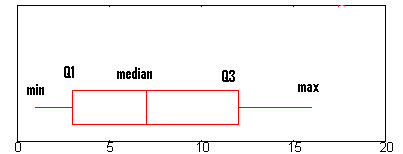
Beispielfrage: Finden Sie den Interquartilsbereich für den obigen Boxplot.

• Schritt 1: Finden Sie Q1.Q1 wird durch den linken Rand der „Box“ dargestellt (an dem Punkt, an dem der Whisker aufhört).
  

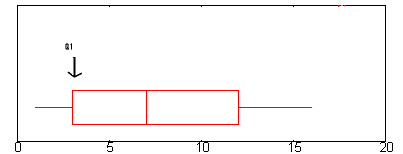
  In der obigen Grafik liegt Q1 ungefähr bei 2,6. (Eine vollständige Erklärung von Q1 finden Sie hier: Die Fünf-Zahlen-Zusammenfassung.)

• Schritt 2: Finden Sie Q3.
  Q3 wird auf einem Boxplot durch den rechten Rand der „Box“ dargestellt.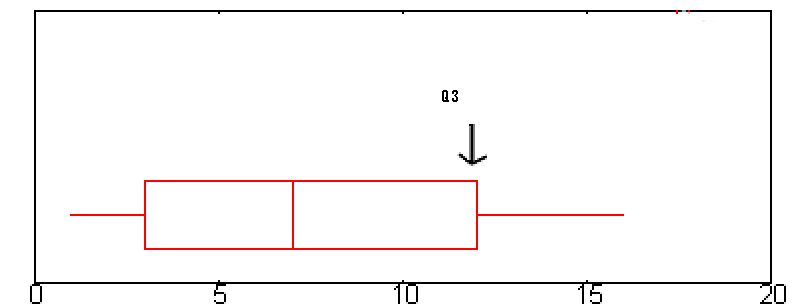
  
  Q3 ist in diesem Diagramm ungefähr 12.
• Schritt 3: Subtrahieren Sie die Zahl, die Sie in Schritt 1 gefunden haben, von der Zahl, die Sie in Schritt 3 gefunden haben.
  So erhalten Sie den Interquartilsbereich. 12 – 2,6 = 9,4.

Das war’s!

Zurück zum Anfang

Interquartilsbereich in Minitab

Lesen Sie weiter, um eine Schritt-für-Schritt-Anleitung zu erhalten, oder sehen Sie sich die Video-Version unten an.

Interquartilsbereich in Minitab: Schritte

Beispielfrage: Finden Sie in Minitab einen Interquartilsbereich für den Notendurchschnitt (GPA) im folgenden Datensatz:
Notendurchschnitt (GPA): 1(3,2), 1(3,1), 2(3,5), 2(2,0), 3(1.9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5(3.3), 6(3.4), 6(2.6), 6(2.5), 7(2.0), 7(1.5), 8(4.0), 8(2.0).

Schritt 1: Geben Sie Ihre Daten in ein Minitab Arbeitsblatt ein. Geben Sie Ihre Daten in eine oder zwei Spalten ein.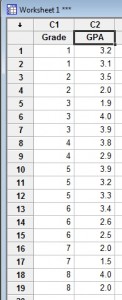

Schritt 2: Klicken Sie auf „Statistik“, dann auf „Grundlegende Statistik“ und anschließend auf „Deskriptive Statistik anzeigen“, um das Menü „Deskriptive Statistik“ zu öffnen.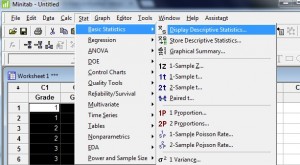

Schritt 3: Klicken Sie auf einen Variablennamen im linken Fenster und dann auf die Schaltfläche „Auswählen“, um den Variablennamen in das rechte Fenster zu übertragen.

Schritt 4: Klicken Sie auf die Schaltfläche „Statistik“.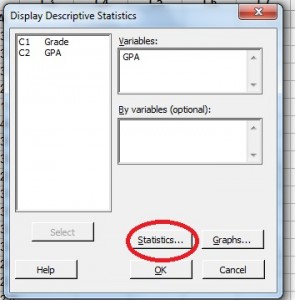

Schritt 5: Markieren Sie „Interquartile Range.“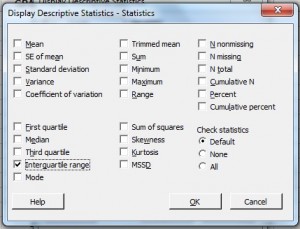
.

Schritt 6: Klicken Sie auf die Schaltfläche „OK“ (es öffnet sich ein neues Fenster mit dem Ergebnis). Der IQR für den GPA in diesem speziellen Datensatz ist 1,8.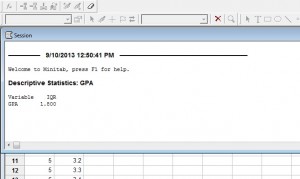

Das war’s!

Tipp: Wenn Sie keine anschauliche Statistik in einem Fenster angezeigt bekommen, klicken Sie in der Symbolleiste auf „Fenster“ und dann auf „Kacheln“. Klicken Sie auf das Sitzungsfenster (hier wird die deskriptive Statistik angezeigt) und scrollen Sie dann nach oben, um Ihre Ergebnisse zu sehen.

Zurück zum Anfang

Wie man einen Interquartilsbereich in Excel 2007 findet

Schauen Sie sich das Video an oder lesen Sie die folgenden Schritte, um einen Interquartilsbereich in Excel 2007 zu finden:

Schritte:
Schritt 1: Geben Sie Ihre Daten in eine einzelne Excel-Spalte auf einem Arbeitsblatt ein. Geben Sie Ihre Daten zum Beispiel in die Zellen A2 bis A10 ein. Lassen Sie keine Lücken in Ihren Daten.

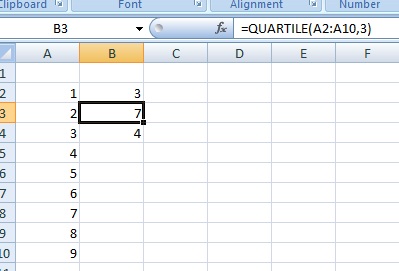
Schritt 2: Klicken Sie auf eine leere Zelle (z. B. auf Zelle B2) und geben Sie dann =QUARTILE(A2:A10,1) ein. Sie müssen A2:A10 durch die tatsächlichen Werte aus Ihrem Datensatz ersetzen. Wenn Sie Ihre Daten zum Beispiel in B2 bis B50 eingegeben haben, lautet die Gleichung =QUARTILE(B2:B50,1). Die „1“ in dieser Excel-Formel(A2:A10,1) steht für das erste Quartil (d. h. den Punkt, der bei 25 % des Datensatzes liegt).

Schritt 3: Klicken Sie auf eine zweite leere Zelle (z. B. auf Zelle B3) und geben Sie dann =QUARTILE(A2:A10,3) ein. Ersetzen Sie A2:A10 durch die tatsächlichen Werte aus Ihrem Datensatz. Die „3“ in dieser Excel-Formel (A2:A10,3) steht für das dritte Quartil (d. h. den Punkt, der bei 75 % des Datensatzes liegt).

Schritt 4: Klicken Sie auf eine dritte leere Zelle (z. B. auf Zelle B4) und geben Sie dann =B3-B2 ein. Wenn sich Ihre Quartilsfunktionen aus Schritt 2 und 3 an unterschiedlichen Stellen befinden, ändern Sie die Zellbezüge.

Schritt 5: Drücken Sie die „Enter“-Taste. Excel gibt den IQR in der Zelle zurück, auf die Sie in Schritt 4 geklickt haben

Das war’s!

Zurück zum Anfang

Wie man einen Interquartilsbereich in SPSS findet

Wie die meisten Technologien verfügt SPSS über mehrere Möglichkeiten, wie Sie den IQR berechnen können. Wenn Sie jedoch auf den intuitivsten Weg klicken, den Sie erwarten würden, um ihn zu finden („Deskriptive Statistik > Häufigkeiten“), ist die Überraschung, dass der IQR nicht aufgelistet wird (obwohl er das erste, zweite und dritte Quartil auflistet). Sie könnten diesen Weg nehmen und dann das dritte Quartil vom ersten subtrahieren, um den IQR zu erhalten. Der einfachste Weg, den Interquartilsbereich in SPSS zu finden, ist jedoch die Verwendung des Befehls „Explore“. Wenn Sie bereits Daten in Ihr Arbeitsblatt eingegeben haben, springen Sie zu Schritt 3.

Schauen Sie sich das Video an oder lesen Sie die folgenden Schritte:

Schritte

Schritt 1: Öffnen Sie eine neue Datendatei in SPSS. Klicken Sie auf „Datei“, fahren Sie mit der Maus über „Neu“ und klicken Sie dann auf „Daten“.

Schritt 2: Geben Sie Ihre Daten in die Spalten des Arbeitsblatts ein. Sie können so viele Spalten verwenden, wie Sie benötigen, aber lassen Sie keine leeren Zeilen oder Leerzeichen zwischen Ihren Daten. Siehe: So geben Sie Daten in SPSS ein.

Schritt 3: Klicken Sie auf „Analysieren“, dann mit der Maus auf „Deskriptive Statistik“. Klicken Sie auf „Erkunden“, um das Dialogfeld „Erkunden“ zu öffnen.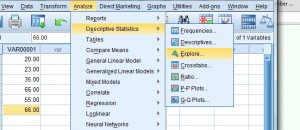

Schritt 4: Klicken Sie auf den Variablennamen (das ist nur ein schicker Name für die Spaltenüberschrift) und dann auf den oberen Pfeil, um die Variable in das Feld „Abhängige Liste“ zu verschieben.

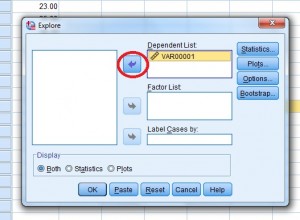
Das Dialogfeld „Variablen erkunden“.

Schritt 5: Klicken Sie auf „OK“. Der Interquartilsbereich wird im Feld „Beschreibungen“ aufgelistet.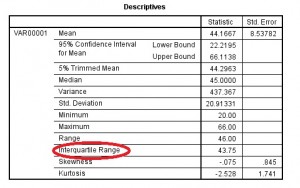

Tipp: In diesem Beispiel ist nur eine Liste in das Datenblatt eingegeben, aber Sie haben möglicherweise mehrere zur Auswahl, je nachdem, wie Sie Ihre Daten eingegeben haben. Stellen Sie sicher, dass Sie die richtige Variable (Spaltennamen) auswählen, bevor Sie fortfahren. Wenn Sie einprägsamere Variablennamen wünschen, ändern Sie den Spaltentitel, indem Sie auf die Schaltfläche „Variablenansicht“ ganz unten links auf dem Arbeitsblatt klicken. Geben Sie Ihren neuen Variablennamen ein und kehren Sie dann zur Datenansicht zurück, indem Sie auf die Schaltfläche „Datenansicht“ klicken.
Zurück zum Anfang

Was ist ein Interquartilsbereich?

Stellen Sie sich alle Daten in einer Menge als Punkte auf einer Zahlenlinie vor. Wenn Sie zum Beispiel 3, 7 und 28 in Ihrem Datensatz haben, stellen Sie sich diese als Punkte auf einer Zahlengeraden vor, die auf 0 zentriert ist, sich aber sowohl unendlich unter als auch unendlich über Null ausdehnt. Einmal auf dieser Zahlengeraden aufgetragen, bilden der kleinste Datenpunkt und der größte Datenpunkt im Datensatz die Grenzen (d. h. eine untere und eine obere Grenze) eines Intervalls auf der Zahlengeraden, das alle Datenpunkte im Satz enthält. Der Interquartilsbereich (IQR) ist die Länge der mittleren 50% dieses Raumintervalls.

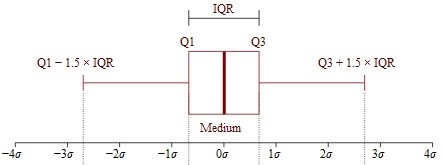
Der Interquartilsbereich ist die mittleren 50% eines Datensatzes. Box and whiskers image by Jhguch at en.wikipedia

Wenn Sie wissen wollen, was der IQR formal gesehen ist, wird der IQR berechnet als: Die Differenz zwischen dem dritten oder oberen Quartil und dem ersten oder unteren Quartil. Quartil ist ein Begriff, der verwendet wird, um zu beschreiben, wie man den Datensatz in vier gleiche Portionen unterteilt (denken Sie an Viertel).

IQR-Beispiel

Wenn Sie eine Menge haben, die die Datenpunkte 1, 3, 5, 7, 8, 10, 11 und 13 enthält, ist das erste Quartil 4, das zweite Quartil ist 7,5 und das dritte Quartil ist 10,5. Zeichnen Sie diese Punkte auf eine Zahlenlinie und Sie werden sehen, dass diese drei Zahlen die Zahlenlinie in Quartile von 1 bis 13 unterteilen. Der IQR dieses Datensatzes ist also 6,5, berechnet als 10,5 minus 4. Das erste und das dritte Quartil werden manchmal auch als 25. und 75. Perzentil bezeichnet, da dies die entsprechenden Zahlen sind, wenn der Datensatz in Prozente und nicht in Quartale unterteilt wird.

Zurück zum Anfang

Interquartilsbereich mit dem TI83

Schauen Sie sich das Video an oder lesen Sie die folgenden Schritte:

Während Sie den eleganten Online-Interquartilsbereich-Rechner auf dieser Website verwenden können, ist das in einem Quiz oder Test möglicherweise keine Option. Die meisten Dozenten erlauben die Verwendung eines TI-83 in Tests, und er ist sogar einer der wenigen Rechner, die in der AP-Statistikprüfung erlaubt sind. Um den Interquartilsbereich des TI 83 zu finden, müssen Sie lediglich Ihre Datenliste eingeben und ein paar Tasten drücken.

Beispielproblem: Finden Sie den Interquartilsbereich des TI 83 für die Höhen der 10 höchsten Gebäude der Welt (Stand: 2009). Die Höhen (in Fuß) sind: 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272.

Schritte

Schritt 1: Geben Sie die obigen Daten in eine Liste auf dem TI 83 Taschenrechner ein. Drücken Sie die Taste STAT und dann die Taste ENTER. Geben Sie die erste Zahl (2717) ein, und drücken Sie dann ENTER. Fahren Sie mit der Eingabe von Zahlen fort und drücken Sie nach jeder Eingabe ENTER.

Schritt 2: Drücken Sie die STAT-Taste.

Schritt 3: Drücken Sie die rechte Pfeiltaste (die Pfeiltasten befinden sich oben rechts auf dem Tastenfeld), um „Calc.“

Schritt 4: Drücken Sie ENTER, um „1-Var Stats“ zu markieren.

Schritt 5: Drücken Sie erneut ENTER, um eine Liste der Stats aufzurufen.

Schritt 6: Blättern Sie mit den Pfeiltasten in der Liste nach unten, um Q1 und Q3 zu finden. Schreiben Sie diese Zahlen auf. Sie könnten die Zahlen kopieren und einfügen, aber leider macht Texas Instruments dies nicht einfach:

1. Benutzen Sie die Pfeiltasten, um den Cursor an den Anfang des
   Textes zu setzen, den Sie hervorheben möchten.
2. Benutzen Sie die TI-Tastatur, drücken und halten Sie die Umschalttaste und benutzen Sie dann die Pfeiltasten, um den Text zu markieren.
3. Lassen Sie die Umschalttaste und die Pfeiltaste los.

Es sollte das Menü „Kopieren und Einfügen“ erscheinen, mit dem Sie die Daten kopieren und einfügen können. Sie müssten dies zweimal tun (und jedes Mal zum HOME-Bildschirm zurückkehren), daher ist es viel schneller, die Zahlen einfach aufzuschreiben.

Schritt 7: Subtrahieren Sie Q1 von Q3, um den IQR zu finden (strong>624 Fuß für diesen Satz von Zahlen).

Das war’s!
Zurück zum Anfang

Wie man Q1, Q3 und den Interquartilsbereich TI 89 findet

Schauen Sie sich das Video an oder lesen Sie die Schritte unten:

Beispielproblem: Finden Sie Q1, Q3 und den IQR für die folgende Liste von Zahlen: 1, 9, 2, 3, 7, 8, 9, 2.

Schritt 1: Drücken Sie APPS. Blättern Sie zu Statistiken/Listeneditor (verwenden Sie zum Blättern die Pfeiltasten auf dem Tastenfeld). Drücken Sie ENTER. Wenn Sie den Statistik-/Listeneditor nicht haben, können Sie ihn hier herunterladen.

Schritt 2: Löschen Sie die Daten im Listeneditor: Drücken Sie F1 8.

Schritt 3: Drücken Sie ALPHA 9 ALPHA 1 ENTER. Dies gibt Ihrer Liste den Namen „IQ“.

Schritt 4: Geben Sie Ihre Zahlen ein, eine nach der anderen. Nach jeder Eingabe drücken Sie die ENTER-Taste. Für unsere Zahlengruppe geben Sie
1,9,2,3,7,8,9,2

Schritt 5: Drücken Sie F4 und dann ENTER (für den 1-Var-Statistikbildschirm).

Schritt 6: Teilen Sie dem Rechner mit, dass Sie Statistiken für die Liste „IQ“ wünschen, indem Sie ALPHA 9 ALPHA 1 in das Feld „Liste:“ eingeben. Der Rechner sollte den Cursor automatisch für Sie dorthin setzen. Drücken Sie zweimal ENTER.

Schritt 7: Lesen Sie die Ergebnisse. Q1 wird als Q1X aufgelistet (in unserem Beispiel Q1X=2). Q3 wird als Q3X aufgeführt (Q3X=8,5). Um den IQR zu ermitteln, subtrahieren Sie Q1 von Q3 auf dem Startbildschirm. Der IQR ist 8,5-2=6,5.

Das war’s!

Zurück zum Seitenanfang

Was ist die Interquartilsbereichsformel?

Die IQR-Formel lautet:
IQR = Q3 – Q1

Wobei Q3 das obere Quartil und Q1 das untere Quartil ist.

IQR als Test auf Normalverteilung

Die Interquartilsbereichsformel kann zusammen mit dem Mittelwert und der Standardabweichung verwendet werden, um zu testen, ob eine Grundgesamtheit eine Normalverteilung aufweist oder nicht. Die Formeln, um festzustellen, ob eine Population normalverteilt ist oder nicht, lauten:
Q1 – (σ z1) + X
Q3 – (σ z3) + X
Wobei Q1 das erste Quartil, Q3 das dritte Quartil, σ die Standardabweichung, z der Standardwert („z-score“) und X der Mittelwert ist. Um festzustellen, ob eine Grundgesamtheit normalverteilt ist, lösen Sie beide Gleichungen und vergleichen dann die Ergebnisse. Gibt es einen signifikanten Unterschied zwischen den Ergebnissen und dem ersten oder dritten Quartil, dann ist die Grundgesamtheit nicht normalverteilt.

Zurück zum Anfang

Wofür wird ein Interquartilsbereich verwendet?

Der IQR wird verwendet, um zu messen, wie weit die Datenpunkte in einem Satz vom Mittelwert des Datensatzes entfernt sind. Je höher der IQR ist, desto weiter liegen die Datenpunkte auseinander; im Gegensatz dazu sind die Datenpunkte um den Mittelwert herum umso mehr gebündelt, je kleiner der IQR ist. Der IQR-Bereich ist eine von vielen Messungen, die verwendet werden, um zu messen, wie weit die Datenpunkte in einem Datensatz verstreut sind. Er wird am besten zusammen mit anderen Messungen wie dem Median und dem Gesamtbereich verwendet, um ein vollständiges Bild von der Tendenz eines Datensatzes zu erhalten, sich um seinen Mittelwert zu gruppieren.
Zurück zum Anfang

Woher kommt der Begriff Interquartilsbereich?

Wer hat den Begriff „Interquartilsbereich“ erfunden? Um das herauszufinden, müssen wir bis ins 19. Jahrhundert zurückgehen.

Geschichte

Der britische Arzt Sir Donald MacAlister verwendete die Begriffe unteres Quartil und höheres Quartil in der 1879 erschienenen Publikation „The Law of the Geometric Mean. Proc. R. Soc. XXIX, S. 374: „Da diese beiden Maße, zusammen mit dem Mittelwert, die Kurve der Anlage in vier gleiche Teile teilen, schlage ich vor, sie ‚höheres Quartil‘ bzw. ‚unteres Quartil‘ zu nennen.“

Obwohl von Beruf Arzt, war er mathematisch begabt und erreichte 1877 die höchste Punktzahl in den abschließenden Mathematikprüfungen an der Universität Cambridge. Er sprach neunzehn Sprachen, darunter Englisch, Tschechisch und Schwedisch.

Macalisters Arbeit, das Gesetz des geometrischen Mittels, war eigentlich eine Antwort auf eine Frage von Francis Galton (Erfinder des Galton-Boards). Aber erst 1882 verwendete Galton („Report of the Anthropometric Committee“) die Werte des oberen und unteren Quartils und den Begriff „Interquartilsbereich“ – definiert als das Doppelte des wahrscheinlichen Fehlers. Galton war nicht nur Statistiker, sondern auch Anthropologe, Geograph, Protogenetiker und Psychometriker, der mehr als 340 Bücher veröffentlichte. Er prägte auch die statistischen Begriffe „Korrelation“ und „Regression zum Mittelwert“.

Gonick, L. und Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, S. 20-21, 1993.

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study erhalten Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf diesem Gebiet. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!