Heading

Im Jahr 1072 n. Chr. dokumentierte Omar Khayyam die genaueste jemals berechnete Jahreslänge – eine Zahl, die für die meisten Zwecke in der modernen Welt immer noch genau genug ist. Khayyam war ein Astronom, Astrologe, Arzt, Philosoph und Mathematiker: Er leistete herausragende Beiträge zur Algebra. Seine Poesie ist im Westen bekannter als die jedes anderen nicht-westlichen Dichters.

Der Mann selbst bleibt etwas rätselhaft. Verschiedene Biographen haben ihn als einen lebenslustigen, Wein trinkenden Agnostiker, einen heimlichen Zoroastrier, einen Sufi-Muslim, einen orthodoxen sunnitischen Moslem und einen Anhänger der antiken griechischen Philosophie beschrieben. Alle sind sich einig, dass er ein herausragender Intellektueller war.

Anfänge

Omar Khayyam wurde am 18. Mai 1048 in der großen Handelsstadt Nishapur in Nordpersien geboren. Heute liegt die Stadt im Iran. Omars Vater war Ebrahim Khayyami, ein wohlhabender Arzt. Der Name von Omars Mutter ist nicht bekannt. Einige Autoren haben geschrieben, dass Omars Vater seinen Lebensunterhalt mit der Herstellung von Zelten verdiente, denn Khayyami bedeutet „Zeltmacher“. Aber auch wenn viele Engländer Smith heißen, bedeutet das nicht, dass ihre Väter ihre Tage damit verbrachten, heißes Metall auf einen Amboss zu hämmern.

Omars Familie war muslimisch. Sein Vater scheint der Religion gegenüber entspannt gewesen zu sein und stellte einen Mathematiker namens Bahmanyar bin Marzban, einen Anhänger der alten persischen Religion des Zoroastrismus, als Tutor für Omar ein. Bahmanyar war ein Schüler des großen Arztes, Wissenschaftlers und Philosophen Avicenna gewesen, und er gab Omar eine gründliche Ausbildung in Wissenschaft, Philosophie und Mathematik. Khawjah al-Anbari lehrte Omar Astronomie und führte ihn durch Ptolemäus‘ Almagest.

In seiner frühen Jugend arbeitete Omar in der Praxis seines Vaters und lernte etwas über Medizin.

Omar Khayyam feierte seinen achtzehnten Geburtstag im Jahr 1066. Im selben Jahr erschien der Halleysche Komet am Himmel, die normannische Armee von Wilhelm dem Eroberer fiel in England ein und Omars Vater Ebrahim starb. Wenige Monate nach Ebrahims Tod starb auch Omars Hauslehrer Bahmanyar.

Es war das Ende einer Ära im Leben von Omar Khayyam. Es war an der Zeit, die Angelegenheiten seiner Familie zu ordnen und weiterzuziehen.

Samarkand

Omar Khayyam schloss sich einer der regelmäßigen Karawanen an, die eine dreimonatige Reise von Nishapur in die große Stadt Samarkand machten, die heute in Usbekistan liegt. Samarkand war ein Zentrum der Gelehrsamkeit, und Khayyam kam dort wahrscheinlich im Jahr 1068 im Alter von 20 Jahren an.

In Samarkand nahm er Kontakt mit dem alten Freund seines Vaters Abu Tahir auf, der Gouverneur und oberster Richter der Stadt war. Tahir, der Khayyams außerordentliches Talent im Umgang mit Zahlen bemerkte, gab ihm einen Job in seinem Büro. Bald erhielt Khayyam eine Stelle in der Schatzkammer des Königs.

Während er in Samarkand lebte, machte Khayyam einen großen Fortschritt in der Algebra.

Omar Khayyams Beiträge zur Wissenschaft

Algebra

In der Schule lernen wir Gleichungen der Form ax2 + bx + c = 0; diese werden quadratische Gleichungen genannt. Kubische Gleichungen haben die Form ax3 + bx2 + cx + d = 0. Natürlich sind kubische Gleichungen schwieriger zu lösen als quadratische.

Khayyam vermutete richtig, dass es nicht möglich ist, kubische Gleichungen mit den traditionellen altgriechischen geometrischen Werkzeugen von Lineal und Zirkel zu lösen. Andere Methoden sind erforderlich.

Im Alter von 22 Jahren, im Jahr 1070, veröffentlichte Khayyam eines seiner größten Werke: Treatise on Demonstration of Problems of Algebra and Balancing. Darin zeigte er, dass eine kubische Gleichung mehr als eine Lösung haben kann. Er zeigte auch, wie die Schnittpunkte von Kegelschnitten wie Parabeln und Kreisen genutzt werden können, um geometrische Lösungen von kubischen Gleichungen zu erhalten. Archimedes hatte tatsächlich begonnen Arbeit in diesem Bereich über tausend Jahre früher, als er als das spezifische Problem der Suche nach dem Verhältnis des Volumens von einem Teil einer Kugel zu einem anderen. Khayyam betrachtete das Problem auf eine allgemeinere, methodischere Weise.

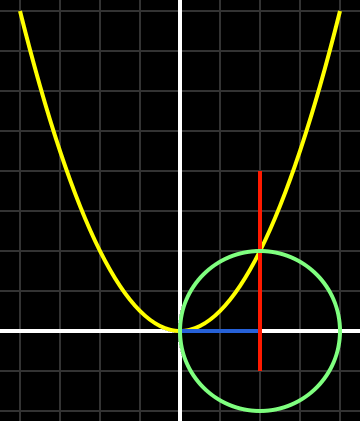
In der Sprache der modernen Mathematik zeigt Khayyams Lösung der Gleichung x3 + a2x = b eine Parabel der Gleichung x2 = ay, einen Kreis mit dem Durchmesser b/a2 und eine senkrechte Linie durch den Schnittpunkt. Die Lösung ist durch den Abstand auf der x-Achse zwischen dem Ursprung und der (roten) senkrechten Linie gegeben. Bild von Pieter Kuiper.

Khayyams Lösungen vermieden negative Koeffizienten und negative Wurzeln, weil negative Zahlen in der islamischen Mathematik nicht anerkannt waren. (Einige Kulturen hatten jedoch negative Zahlen in die Mathematik aufgenommen – zum Beispiel hatte Brahmagupta 400 Jahre zuvor negative Zahlen in die indische Mathematik eingeführt.)

Obwohl Khayyams Leistung großartig war, war er persönlich enttäuscht, dass er die Geometrie einsetzen musste, um kubische Gleichungen zu lösen – er hatte gehofft, einen Algorithmus zu entdecken, der nur Algebra verwendet.

Die Abhandlung über die Demonstration von Problemen der Algebra und des Gleichgewichts etablierte Khayyam als einen Mathematiker ersten Ranges, und sein Ruf verbreitete sich schnell in ganz Persien.

Nach Khayyams Durchbruch gab es kaum nennenswerte Fortschritte bei kubischen Gleichungen bis 1535, als Niccolo Tartaglia allgemeine Lösungen für alle kubischen Gleichungen fand.

Khayyams Algebra war nicht das System von Buchstaben und Zeichen, das wir heute verwenden. Seine Algebra wurde in Worten ausgedrückt. Wo wir heute also schreiben:

Lösen Sie für x:

x2 + 6 = 5x

Khayyam schrieb: Wie groß ist ein Quadrat, so dass es, wenn man 6 Dirham dazu addiert, gleich der fünften Wurzel dieses Quadrats wird?

Verknüpfung von Algebra und Geometrie

Algebra und Geometrie wurden von Pierre de Fermat und René Descartes im 16. Jahrhundert erfolgreich verknüpft, was zum modernen x-y-Koordinatensystem führte.

Khayyams Arbeit mit Würfeln hatte ihn davon überzeugt, dass Algebra und Geometrie miteinander verbunden sind, und er zitierte Euklids Elemente, um die Idee zu unterstützen:

Wer glaubt, Algebra sei ein Trick, um Unbekannte zu erhalten, hat vergeblich gedacht. Es sollte nicht beachtet werden, dass Algebra und Geometrie sich äußerlich unterscheiden. Algebren sind geometrische Tatsachen, die durch die Sätze 5 und 6 des Buches 2 der Elemente von Euklid bewiesen werden.

Jahreslänge

Im Jahr 1073 erhielt Khayyam eine Einladung in die persische Stadt Isfahan, der Hauptstadt des Seldschukenreiches, um einen Kalender zu erstellen, der geordnet funktionieren und für immer genau sein sollte – dies war eine Zeit, in der die Jahreslängen regelmäßig geändert wurden.

Khayyams Einladung kam von den beiden mächtigsten Männern des Seldschukenreiches, zu dem Persien gehörte: Das waren Malik Shah, der Sultan des Reiches, und Nizam al-Mulk, sein Wesir.

Khayyam rekrutierte andere talentierte Wissenschaftler, die ihn 1074 nach Isfahan begleiteten. Dort wurde ihm ein außerordentlich hohes Gehalt gezahlt und er genoss einen privilegierten Lebensstil. Malik Shah bezahlte Khayyam, um ein Observatorium zu gründen, das zunächst 30 Jahre lang Himmelsbeobachtungen machen sollte. In dieser Zeit sollte Saturn, der damals am weitesten entfernte Planet, eine Umlaufbahn vollenden.

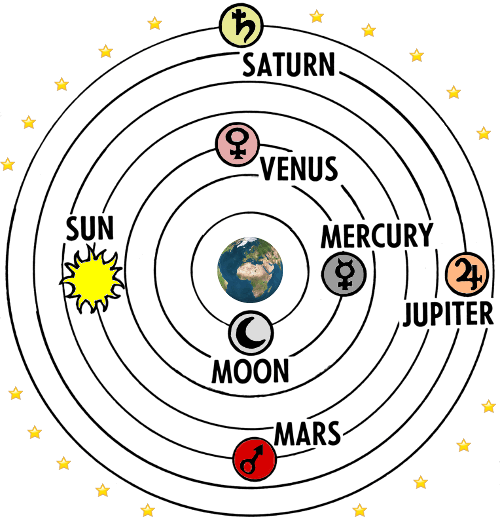
Ptolemäus‘ Universum – das von Omar Khayyam akzeptierte Modell.

Während seiner Zeit in Isfahan maß Khayyam die Länge eines Jahres – genauer gesagt die tropische Jahreslänge – mit bemerkenswerter Genauigkeit und Präzision.

Khayyam fand heraus, dass 1.029.983 Tage 2.820 Jahre ergeben. Das ergibt eine tropische Jahreslänge von 365,2422 Tagen auf sieben signifikante Stellen genau. Obwohl es Mode geworden ist, mehr Nachkommastellen als diese anzugeben, enthält Khayyams Eingabe von 1.029.983 Tagen sieben signifikante Ziffern, so dass es unvernünftig ist, mehr als diese Anzahl signifikanter Ziffern in der berechneten Jahreslänge anzugeben.

Heute wissen wir, dass sich die Länge eines tropischen Jahres tatsächlich von Jahr zu Jahr um bis zu 30 Minuten ändert. Die durchschnittliche Länge eines tropischen Jahres, die heute angegeben wird, beträgt 365,242189 Tage, was auf sieben signifikante Ziffern genau 365,2422 Tage ergibt – genau die Zahl, auf die Khayyam vor fast tausend Jahren kam. Die Länge eines tropischen Jahres nimmt im Laufe der Zeit ebenfalls leicht zu, wenn auch nicht genug zwischen Khayyams Ära und der unseren, um auf einer Skala von sieben signifikanten Zahlen aufzufallen.

Malik Shah führte Khayyams neuen Kalender im Seldschukenreich am 15. März 1079 ein. Er wurde bis ins 20. Jahrhundert verwendet.

Das Parallelpostulat

Die 13 Bücher von Euklids Elementen, die um 300 v. Chr. veröffentlicht wurden, waren wohl die einflussreichsten Bücher in der gesamten Geschichte der Mathematik. Die Elemente waren auf fünf geometrischen Postulaten aufgebaut – also fünf Dingen, von denen man annahm, dass sie in der Geometrie wahr sind: zum Beispiel, dass alle rechten Winkel gleich sind.

Das fünfte von Euklids fünf Postulaten war das Parallelitätspostulat. Das Parallelitätspostulat war für Jahrtausende eine Quelle der Verwirrung, der Irritation und der Freude für Mathematiker. Die Freude war meist nur von kurzer Dauer und gehörte Mathematikern, die glaubten, das Postulat bewiesen zu haben, nur um dann enttäuscht zu sein, wenn ein Fehler in ihrem ‚Beweis‘ entdeckt wurde.

Euklid hatte eine gerade Linie betrachtet, die zwei andere gerade Linien kreuzt. Er betrachtete die Situation, wenn sich die Innenwinkel (im Bild unten) zu weniger als 180 Grad addieren. Unter diesen Umständen sagte er, dass sich die beiden Geraden schließlich auf der Seite der beiden Winkel treffen werden, die sich zu weniger als 180 Grad addieren.

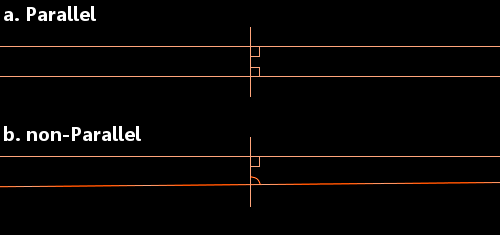
a. Wenn jeder Winkel 90 Grad beträgt, sind die Linien parallel.
b. Wenn einer oder beide Winkel kleiner als 90 Grad sind, treffen sich die Linien.

Seit der Zeit der ersten Veröffentlichung der Elemente hatten Mathematiker versucht, Euklids erste vier Postulate zu verwenden, um das Parallelitätspostulat zu beweisen. Sie waren zum Scheitern verurteilt. Wir wissen heute, dass es unmöglich ist, das Parallelenpostulat mit Hilfe der anderen Postulate Euklids zu beweisen.

Omar Khayyam’s Versuch war interessant. In seinen Erläuterungen zu den Schwierigkeiten bei den Postulaten in Euklids Elementen bittet er seine Leser, eine gerade Linie AB zu betrachten:

Er bittet seine Leser, zwei gleiche Linien zu betrachten, die senkrecht auf AB stehen und sieht drei mögliche Anordnungen, die vierseitige Figuren ergeben können:

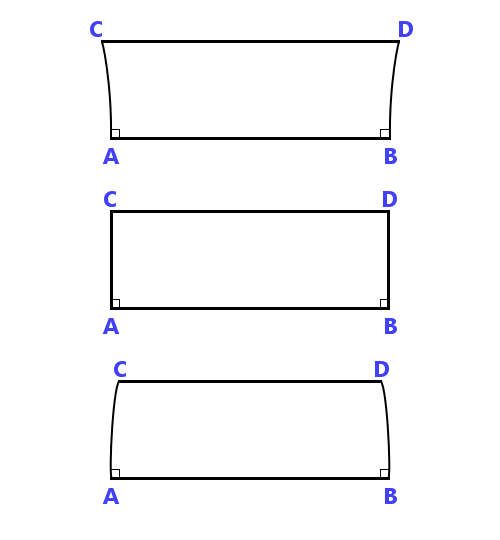
Dann widerlegt er die Möglichkeit, dass die Winkel C und/oder D etwas anderes als rechte Winkel sein können, und in der obigen Abbildung ist nur die mittlere Option möglich. Er glaubt also, er habe das Parallelitätspostulat bewiesen. In Wirklichkeit hat er das nicht getan, er hat es nur anders formuliert.

Was für Mathematikhistoriker interessant ist, ist, dass sie in Khayyams Ideen – die in den obigen Bildern grob dargestellt sind – die ersten Schimmer der nicht-euklidischen Geometrie sehen können.

Einige persönliche Details und das Ende

Vollständige Details über Khayyams persönliches Leben sind nicht bekannt. Es wird angenommen, dass er verheiratet war und mindestens einen Sohn und eine Tochter hatte.

Im Jahr 1092 starben sowohl Malik Schah als auch sein Wesir – der erste wahrscheinlich durch Vergiftung, der zweite durch ein Attentat. Khayyam versteckte sich während des daraus resultierenden Machtkampfes. Sein Überleben hing davon ab, sich bedeckt zu halten. Er war Malik Schahs Leibarzt gewesen und sein enger persönlicher Freund geworden – was ihn zu Feinden gemacht hatte – und Khayyams Poesie deutet darauf hin, dass sein Verhalten nicht unbedingt fromm war – was ihn ebenfalls zu Feinden gemacht hatte. Khayyam hat zu seinen Lebzeiten eigentlich keine Gedichte veröffentlicht. Einige seiner Grübeleien hätten ihn möglicherweise in Lebensgefahr gebracht.

Nach dem Machtkampf dauerte es etwa 20 Jahre, bis Khayyam vollständig rehabilitiert war und er mit 64 Jahren wieder in der Gesellschaft der Mächtigen auftauchte. Allerdings weigerte er sich, zu lehren. Eines seiner Gedichte deutet an, warum das so sein könnte:

Omar Khayyam starb im Alter von 83 Jahren am 4. Dezember 1131 in seiner Heimatstadt Nishapur. Er wurde in einem Grab beigesetzt, dessen Standort er in einem Obstgarten gewählt hatte, in dem zweimal im Jahr die Blüte fiel.

Khayyams Poesie wurde in den 1800er Jahren durch Edward FitzGeralds Übersetzungen in den Rubaiyat von Omar Khayyam popularisiert. Khayyam wurde im Westen so bewundert, dass der Schah von Iran 1963 sein Grab exhumieren ließ und Khayyams Überreste in ein riesiges, eigens errichtetes Mausoleum in Nishapur überführte, wo Touristen dem großen Dichter huldigen können.

Wir wollen mit einem von Khayyams berühmtesten und eindrucksvollsten Vierzeilern enden:

Autor dieser Seite: The Doc
Die Bilder wurden von dieser Website digital bearbeitet und koloriert. © Alle Rechte vorbehalten.

Diese Seite zitieren

Bitte verwenden Sie die folgende MLA-konforme Zitation:

"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.

Veröffentlicht von FamousScientists.org

Weitere Literatur
Edward FitzGerald (Übersetzer)
The Rubaiyat of Omar Khayyam
Howard Willford Bell, 1901

Victor J. Katz
A History of Mathematics: An Introduction
HarperCollins College Publishers, New York, 1993

Roshdi Rashed (Editor)
Encyclopedia of the History of Arabic science
Routledge, 1996

Geschichte der Astronomie – Mittlerer Osten
ephemeris.com, 2003

Hazhir Teimourian
Omar Khayyam: Poet, Rebel, Astronom
The History Press, 2008

Mehdi Aminrazavi
The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam
Oneworld Publications, 2013