Lernziele
Am Ende dieses Abschnitts werden Sie in der Lage sein:
- Definieren Sie nichtkonservative Kräfte und erklären Sie, wie sie mechanische Energie beeinflussen.
- Zeigen Sie, wie der Energieerhaltungssatz angewendet werden kann, indem Sie die konservativen Kräfte in Bezug auf ihre potenziellen Energien und alle nichtkonservativen Kräfte in Bezug auf die von ihnen verrichtete Arbeit behandeln.
Nichtkonservative Kräfte und Reibung
Kräfte sind entweder konservativ oder nichtkonservativ. Konservative Kräfte wurden in Konservative Kräfte und potentielle Energie besprochen. Eine nicht konservative Kraft ist eine, bei der die Arbeit vom zurückgelegten Weg abhängt. Reibung ist ein gutes Beispiel für eine nicht konservative Kraft. Wie in Abbildung 1 dargestellt, hängt die gegen Reibung verrichtete Arbeit von der Länge des Weges zwischen Start- und Endpunkt ab. Aufgrund dieser Abhängigkeit vom Weg gibt es keine potenzielle Energie, die mit nicht konservativen Kräften verbunden ist. Ein wichtiges Merkmal ist, dass die von einer nicht konservativen Kraft geleistete Arbeit einem System mechanische Energie hinzufügt oder entzieht. Reibung zum Beispiel erzeugt thermische Energie, die sich verflüchtigt und dem System Energie entzieht. Darüber hinaus kann die thermische Energie, selbst wenn sie zurückgehalten oder eingefangen wird, nicht vollständig in Arbeit zurückverwandelt werden, so dass sie auch in diesem Sinne verloren oder nicht rückgewinnbar ist.

Abbildung 1. Die Menge des gelöschten fröhlichen Gesichts hängt vom Weg des Radiergummis zwischen den Punkten A und B ab, ebenso wie die gegen die Reibung verrichtete Arbeit. Für den Weg in (a) wird weniger Arbeit verrichtet und weniger von dem Gesicht gelöscht als für den Weg in (b). Die Kraft ist hier die Reibung, und der größte Teil der Arbeit geht in Wärmeenergie über, die anschließend das System verlässt (die glückliche Fläche plus der Radierer). Die aufgewendete Energie kann nicht vollständig zurückgewonnen werden.
Wie nicht-konservative Kräfte die mechanische Energie beeinflussen
Mechanische Energie kann nicht erhalten bleiben, wenn nicht-konservative Kräfte wirken. Wenn z. B. ein Auto durch Reibung auf ebenem Boden zum Stehen gebracht wird, verliert es kinetische Energie, die als thermische Energie dissipiert wird und seine mechanische Energie reduziert. Abbildung 2 vergleicht die Auswirkungen von konservativen und nicht konservativen Kräften. Wir entscheiden uns oft dafür, zunächst einfachere Systeme wie das in Abbildung 2a zu verstehen, bevor wir kompliziertere Systeme wie in Abbildung 2b untersuchen.

Abbildung 2. Vergleich der Auswirkungen von konservativen und nicht konservativen Kräften auf die mechanische Energie eines Systems. (a) Ein System mit nur konservativen Kräften. Wenn ein Stein auf eine Feder fallen gelassen wird, bleibt seine mechanische Energie konstant (unter Vernachlässigung des Luftwiderstands), da die Kraft in der Feder konservativ ist. Die Feder kann den Stein wieder auf seine ursprüngliche Höhe befördern, wo er wieder nur potenzielle Energie aufgrund der Schwerkraft hat. (b) Ein System mit nicht konservativen Kräften. Wenn derselbe Stein auf den Boden fällt, wird er durch nicht-konservative Kräfte gestoppt, die seine mechanische Energie als Wärmeenergie, Schall und Oberflächenverformung zerstreuen. Der Stein hat mechanische Energie verloren.
Wie der Arbeit-Energie-Satz angewendet wird
Betrachten wir nun, welche Form der Arbeit-Energie-Satz annimmt, wenn sowohl konservative als auch nicht-konservative Kräfte wirken. Wir werden sehen, dass die Arbeit, die von nicht-konservativen Kräften verrichtet wird, gleich der Änderung der mechanischen Energie eines Systems ist. Wie in Kinetische Energie und der Arbeit-Energie-Satz beschrieben, besagt der Arbeit-Energie-Satz, dass die Nettoarbeit eines Systems gleich der Änderung seiner kinetischen Energie ist, oder Wnet = ΔKE. Die Nettoarbeit ist die Summe der Arbeit durch nicht-konservative Kräfte plus der Arbeit durch konservative Kräfte. Das heißt,
Wnet = Wnc + Wc,
so dass
Wnc + Wc = ΔKE,
wobei Wnc die Gesamtarbeit aller nichtkonservativen Kräfte und Wc die Gesamtarbeit aller konservativen Kräfte ist.

Abbildung 3. Eine Person schiebt eine Kiste eine Rampe hinauf und verrichtet dabei Arbeit an der Kiste. Reibung und Gravitationskraft (nicht dargestellt) wirken ebenfalls auf die Kiste ein; beide Kräfte wirken dem Schieben der Person entgegen. Wenn die Kiste die Rampe hinaufgeschoben wird, gewinnt sie an mechanischer Energie, was bedeutet, dass die von der Person geleistete Arbeit größer ist als die von der Reibung geleistete Arbeit.
Betrachten Sie Abbildung 3, in der eine Person eine Kiste eine Rampe hinaufschiebt und dabei auf Reibung trifft. Wie im vorherigen Abschnitt stellen wir fest, dass die von einer konservativen Kraft geleistete Arbeit aus einem Verlust an potenzieller Gravitationsenergie stammt, so dass Wc = -ΔPE. Setzt man diese Gleichung in die vorhergehende ein und löst Wnc, so erhält man
Wnc = ΔKE + ΔPE.
Diese Gleichung bedeutet, dass sich die gesamte mechanische Energie (KE + PE) genau um den Betrag der Arbeit ändert, die durch nichtkonservative Kräfte verrichtet wird. In Abbildung 3 ist dies die von der Person geleistete Arbeit abzüglich der durch die Reibung geleisteten Arbeit. Selbst wenn also die Energie für das interessierende System (z. B. die Kiste) nicht konserviert ist, wissen wir, dass eine gleiche Menge an Arbeit geleistet wurde, um die Änderung der gesamten mechanischen Energie zu verursachen.
Wir ordnen Wnc = ΔKE + ΔPE um und erhalten
KEi + PEi + Wnc = KEf + PEf.
Das bedeutet, dass der Betrag der Arbeit, der durch nicht konservative Kräfte geleistet wird, zur mechanischen Energie eines Systems hinzukommt. Wenn Wnc positiv ist, dann wird die mechanische Energie erhöht, z. B. wenn die Person die Kiste die Rampe in Abbildung 3 hinaufschiebt. Wenn Wnc negativ ist, wird die mechanische Energie verringert, z. B. wenn der Stein in Abbildung 2b auf den Boden trifft. Wenn Wnc gleich Null ist, bleibt die mechanische Energie erhalten, und die nicht konservativen Kräfte sind ausgeglichen. Wenn Sie z. B. einen Rasenmäher mit konstanter Geschwindigkeit auf ebenem Boden schieben, wird Ihre geleistete Arbeit durch die Reibungsarbeit aufgehoben, und der Mäher hat eine konstante Energie.
Anwendung der Energieerhaltung bei nicht-konservativen Kräften
Wenn keine Änderung der potentiellen Energie auftritt, läuft die Anwendung von KEi + PEi + Wnc = KEf + PEf auf die Anwendung des Arbeit-Energie-Satzes hinaus, indem die Änderung der kinetischen Energie gleich der Nettoarbeit gesetzt wird, die am System verrichtet wird, was im allgemeinsten Fall sowohl konservative als auch nicht-konservative Kräfte einschließt. Wenn man aber stattdessen versucht, eine Änderung der gesamten mechanischen Energie in Situationen zu finden, die sowohl Änderungen der potentiellen als auch der kinetischen Energie beinhalten, besagt die vorherige Gleichung KE i + PEi + Wnc = KEf + PEf, dass man damit beginnen kann, die Änderung der mechanischen Energie zu finden, die sich nur aus den konservativen Kräften, einschließlich der Änderungen der potentiellen Energie, ergeben hätte, und dazu die Arbeit mit dem richtigen Vorzeichen zu addieren, die von allen beteiligten nicht-konservativen Kräften geleistet wird.
Beispiel 1. Berechnen der zurückgelegten Strecke: Wie weit ein Baseballspieler rutscht
Betrachten Sie die in Abbildung 4 dargestellte Situation, in der ein Baseballspieler auf ebenem Boden zum Stillstand kommt. Berechnen Sie mit Hilfe von Energiebetrachtungen die Strecke, die der 65,0 kg schwere Baseballspieler rutscht, wenn seine Anfangsgeschwindigkeit 6,00 m/s beträgt und die Reibungskraft gegen ihn konstant 450 N beträgt.

Abbildung 4. Der Baseballspieler gleitet in einer Strecke d zum Stillstand. Dabei wird durch Reibung die kinetische Energie des Spielers abgebaut, indem eine Arbeit verrichtet wird, die der anfänglichen kinetischen Energie entspricht.
Strategie
Die Reibung hält den Spieler an, indem sie seine kinetische Energie in andere Formen umwandelt, einschließlich thermischer Energie. Im Sinne des Arbeit-Energie-Satzes wird die durch die Reibung geleistete Arbeit, die negativ ist, zur anfänglichen kinetischen Energie addiert, um sie auf Null zu reduzieren. Die von der Reibung geleistete Arbeit ist negativ, weil f in die entgegengesetzte Richtung der Bewegung geht (d. h. θ = 180º, und somit cos θ = -1). Somit ist Wnc = -fd. Die Gleichung vereinfacht sich zu
\frac{1}{2}{mv_{\text{i}}^2-fd=0\\
oder
fd=\frac{1}{2}{mv_{\text{i}}^2\\.
Diese Gleichung kann nun für den Abstand d gelöst werden.
Lösung
Löst man die vorherige Gleichung für d und setzt bekannte Werte ein, so erhält man
\begin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0\text{ kg})(6.00\text{ m/s})^2}{(2)(450\text{ N})}\text{ }&&2.60\text{ m}\end{array}\
Diskussion
Der wichtigste Punkt dieses Beispiels ist, dass der Betrag der nicht konservativen Arbeit gleich der Änderung der mechanischen Energie ist. Zum Beispiel muss man härter arbeiten, um einen Lastwagen mit seiner großen mechanischen Energie anzuhalten, als um eine Mücke anzuhalten.
Beispiel 2. Berechnen der zurückgelegten Strecke: Hinaufrutschen an einer Steigung
Angenommen, der Spieler aus Beispiel 1 läuft einen Hügel mit einer Steigung von 5,00º hinauf, dessen Oberfläche der im Baseballstadion ähnelt. Der Spieler rutscht mit der gleichen Anfangsgeschwindigkeit. Bestimmen Sie, wie weit er rutscht.

Abbildung 5. Derselbe Baseballspieler rutscht auf einer 5,00º Steigung zum Stillstand.
Strategie
In diesem Fall reduziert die Arbeit, die durch die nicht konservative Reibungskraft auf den Spieler ausgeübt wird, die mechanische Energie, die er hat, von seiner kinetischen Energie bei Höhe Null auf die endgültige mechanische Energie, die er hat, wenn er sich über die Strecke d bewegt, um die Höhe h entlang des Hügels zu erreichen, mit h = d sin 5,00º. Dies wird durch die Gleichung KE + PEi + Wnc = KE f + PEf ausgedrückt.
Lösung
Die durch Reibung verrichtete Arbeit ist wiederum Wnc = -fd; anfangs ist die potentielle Energie PEi = mg – 0 = 0 und die kinetische Energie \text{KE}_{\text{i}}=\frac{1}{2}mv_{\text{i}}^2\\; die Endenergiebeiträge sind KEf = 0 für die kinetische Energie und PEf = mgh = mgd sin θ für die potentielle Energie.
Das Substituieren dieser Werte ergibt
\frac{1}{2}{mv_{\text{i}}^2+0+\left(-fd\right)=0+mgd\sin\theta\
Lösen Sie dies für d, um zu erhalten
\begin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65.0\text{ kg})(6.00\text{ m/s})^2}{450\text{ N}+(65.0\text{ kg})\links(9.80\text{ m/s}^2\rechts)\sin(5.00^{\circ})}\&&2.31\text{ m}\end{array}\
Diskussion
Wie zu erwarten war, rutscht der Spieler eine kürzere Strecke, wenn er bergauf rutscht. Beachten Sie, dass das Problem auch direkt mit den Kräften und dem Arbeitstheorem hätte gelöst werden können, anstatt die potentielle Energie zu verwenden. Bei dieser Methode hätte man die Vektoren der Normalkraft und der Schwerkraft, die sich nicht mehr gegenseitig aufheben, weil sie in unterschiedliche Richtungen zeigen, sowie die Reibung kombinieren müssen, um die Nettokraft zu finden. Man könnte dann die Nettokraft und die Nettoarbeit verwenden, um die Strecke d zu finden, die die kinetische Energie auf Null reduziert. Indem wir die Energieerhaltung anwenden und stattdessen die potenzielle Energie verwenden, müssen wir nur die potenzielle Gravitationsenergie mgh berücksichtigen, ohne die Kraftvektoren zu kombinieren und aufzulösen. Dies vereinfacht die Lösung erheblich.
Verbindungen herstellen: Take-Home Investigation – Bestimmung der Reibung aus dem Bremsweg
Bei diesem Experiment geht es um die Umwandlung der potenziellen Gravitationsenergie in Wärmeenergie. Verwenden Sie das Lineal, das Buch und die Murmel aus dem Abschnitt „Zusammenhänge herstellen“ von Gravitationspotentialenergie. Zusätzlich benötigen Sie einen Schaumstoffbecher mit einem kleinen Loch in der Seite, wie in Abbildung 6 gezeigt. Lassen Sie die Murmel von der 10-cm-Position auf dem Lineal in den Becher rollen, der sich am unteren Ende des Lineals befindet. Messen Sie die Strecke d, die der Becher zurücklegt, bevor er zum Stillstand kommt. Welche Kräfte haben sie zum Stillstand gebracht? Was ist mit der kinetischen Energie der Murmel am unteren Ende des Lineals passiert? Platzieren Sie als nächstes die Murmel an den Positionen 20 cm und 30 cm und messen Sie erneut die Strecke, die der Becher zurücklegt, nachdem die Murmel in ihn hineingekommen ist. Zeichnen Sie die Strecke, die sich der Becher bewegt, gegen die Ausgangsposition der Murmel auf dem Lineal auf. Ist diese Beziehung linear?
Mit einigen einfachen Annahmen können Sie aus diesen Daten den kinetischen Reibungskoeffizienten μk der Tasse auf dem Tisch ermitteln. Die Reibungskraft f auf die Tasse ist μkN, wobei die Normalkraft N nur das Gewicht der Tasse plus der Murmel ist. Die Normalkraft und die Schwerkraft verrichten keine Arbeit, da sie senkrecht zur Verschiebung der Tasse stehen, die sich horizontal bewegt. Die durch Reibung verrichtete Arbeit ist fd. Sie benötigen auch die Masse der Murmel, um ihre anfängliche kinetische Energie zu berechnen.
Es ist interessant, das obige Experiment auch mit einer Stahlmurmel (oder einem Kugellager) durchzuführen. Wenn Sie diese an denselben Stellen auf dem Lineal loslassen wie die Glasmurmel, ist dann die Geschwindigkeit dieser Stahlmurmel die gleiche wie die der Murmel am Boden des Lineals? Ist die Entfernung, die der Becher zurücklegt, proportional zur Masse der Stahl- und der Glasmurmel?

Abbildung 6. Eine Murmel rollt ein Lineal hinunter in einen Schaumstoffbecher.
PhET Explorations: Die Rampe
Erforschen Sie Kräfte, Energie und Arbeit, indem Sie Haushaltsgegenstände eine Rampe hoch- und runterschieben. Senken und heben Sie die Rampe, um zu sehen, wie der Neigungswinkel die parallel wirkenden Kräfte auf den Aktenschrank beeinflusst. Diagramme zeigen Kräfte, Energie und Arbeit.
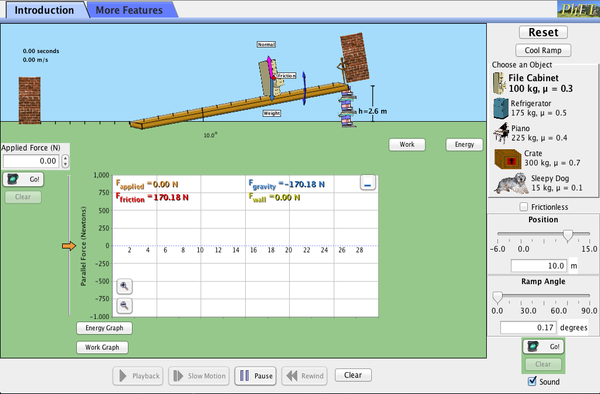
Klicken Sie zum Download. Mit Java ausführen.
Zusammenfassung des Abschnitts
- Eine nicht konservative Kraft ist eine Kraft, bei der die Arbeit vom Weg abhängt.
- Reibung ist ein Beispiel für eine nicht konservative Kraft, die mechanische Energie in thermische Energie umwandelt.
- Die von einer nicht konservativen Kraft verrichtete Arbeit Wnc ändert die mechanische Energie eines Systems. In Gleichungsform ist Wnc = ΔKE + ΔPE oder, äquivalent, KEi + PEi + Wnc = KEf + PEf.
- Wenn sowohl konservative als auch nicht-konservative Kräfte wirken, kann die Energieerhaltung angewandt und verwendet werden, um die Bewegung in Bezug auf die bekannten potenziellen Energien der konservativen Kräfte und die von den nicht-konservativen Kräften geleistete Arbeit zu berechnen, anstatt die Nettoarbeit aus der Nettokraft zu ermitteln oder die Newtonschen Gesetze direkt anwenden zu müssen.
Probleme & Übungen
- Eine 60,0 kg schwere Skiläuferin mit einer Anfangsgeschwindigkeit von 12,0 m/s fährt eine 2,50 m hohe Steigung hinauf, wie in Abbildung 7 dargestellt. Ermitteln Sie ihre Endgeschwindigkeit am Gipfel, wenn der Reibungskoeffizient zwischen den Skiern und dem Schnee 0,0800 beträgt. (Tipp: Ermitteln Sie die zurückgelegte Strecke auf der Steigung unter der Annahme eines geradlinigen Weges, wie in der Abbildung gezeigt.)

Abbildung 7. Die anfängliche kinetische Energie des Skifahrers wird beim Ausrollen auf den Gipfel einer Steigung teilweise verbraucht.
- (a) Wie hoch kann ein Auto einen Hügel hinaufrollen (Motor ausgekuppelt), wenn die durch Reibung verrichtete Arbeit vernachlässigbar ist und seine Anfangsgeschwindigkeit 110 km/h beträgt? (b) Wenn tatsächlich beobachtet wird, dass ein 750 kg schweres Auto mit einer Anfangsgeschwindigkeit von 110 km/h einen Hügel bis zu einer Höhe von 22,0 m über seinem Ausgangspunkt hinaufrollt, wie viel Wärmeenergie wurde dann durch Reibung erzeugt? c) Wie groß ist die durchschnittliche Reibungskraft, wenn der Hügel eine Neigung von 2,5º über der Horizontalen hat?
Glossar
Konservative Kraft: eine Kraft, deren Arbeit vom Weg zwischen der gegebenen Anfangs- und Endkonfiguration abhängt
Reibung: Kraft zwischen Oberflächen, die dem Gleiten einer Oberfläche auf der anderen entgegenwirkt; Reibung wandelt mechanische Energie in thermische Energie um
Ausgewählte Lösungen zu Problemen & Übungen
1. 9,46 m/s