Suivant : 8.5 Les cycles de puissance de Rankine Haut : 8. Les cycles de puissance avec Précédent : 8.3 Le cycle de Carnot Sommaire Index
Jusqu’à présent, nous n’avons considéré que les gaz idéaux et nous voudrions montrer que les propriétés 
, etc. sont de vraies variables d’état et que les 1ère et 2ème lois de la thermodynamique tiennent lorsque le milieu de travail n’est pas un gaz idéal (c’est-à-dire un milieu diphasique). Une façon élégante de le faire est de considérer un cycle de Carnot pour un milieu diphasique. Le fait d’affirmer que tous les moteurs de Carnot fonctionnant entre deux températures données ont le même rendement est une façon d’énoncer la deuxième loi de la thermodynamique. Le fluide de travail ne doit pas nécessairement être un gaz idéal et peut être un milieu diphasique changeant de phase.
L’idée est de faire fonctionner un moteur de Carnot entre les températures 
et
pour un milieu diphasique et de le laisser subir un changement de phase. Nous pouvons alors dériver une relation importante connue sous le nom d’équation de Clausius-Clapeyron, qui donne la pente de la courbe de pression de vapeur. Nous pouvons alors mesurer la courbe de pression de vapeur de diverses substances et comparer la pente mesurée à l’équation de Clausius-Clapeyron. Cela peut alors être considéré comme une preuve expérimentale de la validité générale des 1ère et 2ème lois de la thermodynamique !
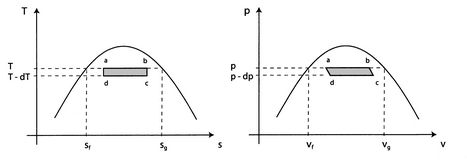
Considérons le cycle infinitésimal de Carnot 
représenté sur laFigure 8.8. La chaleur est absorbée entre les états
et 
. Pour vaporiser une quantité arbitraire de masse, 
, laquantité de chaleur
 |
(8..1) |
doivent être fournis au système. A partir des 1ère et2ème lois de la thermodynamique, le rendement thermiquepour un cycle de Carnot peut être écrit comme
 |
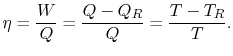Donc, pour le cycle infinitésimal considéré ci-dessus,
 |
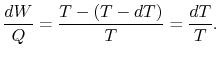(8..2) |
Les travaux le long de 
et 
s’annulent quasiment. s’annulent de sorte que le travail net est la différence entre le travail le long de 
et 
, et 
peut être considérée comme l’aire délimitée par le rectangle :
 |
 |
|
 |
(8..3) |
Substituer les équations (8.1) et(8.3) dans (8.2) onobtient
 |
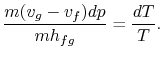L’arrangement des termes donne l’équation de Clausius-Clapeyron,qui définit la pente de la courbe de pression de vapeur :
 |
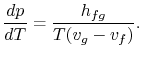(8…4) |
La beauté est que nous avons trouvé une relation générale entre des quantités mesurables expérimentalement à partir de premiers principes(1ère et 2ème lois de la thermodynamique).
Pour tracer la relation Clausius-Clapeyron et la comparer aux courbes de pression de vapeur mesurées expérimentalement, nous devons intégrer l’équation (8.4). Pour ce faire, la chaleur de vaporisation et les volumes spécifiques doivent être des fonctions connues de la température. C’est un problème important en physico-chimie, mais nous ne le poursuivrons pas ici, sauf pour mentionner que si
- les variations de la chaleur de vaporisation peuvent être négligées,
- la phase vapeur est supposée être un gaz idéal, et
- le volume spécifique du liquide est petit par rapport à celui de la phase vapeur,
 |
. |
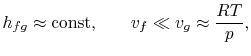L’intégration peut être facilement réalisée8.1. En faisant ces approximations, l’équation de Clausius-Clapeyronequation devient
 |
En effectuant l’intégration, on obtient l’expression suivante :
 |
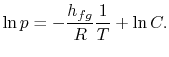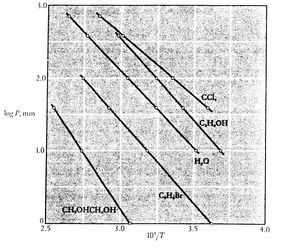
Notez que que les courbes de pression de vapeur sont des lignes droites si 
est tracé en fonction de 
et que la pente des courbes est
, directement liée à la chaleur de vaporisation.Les figures 8.9, 8.9 et 8.22 illustrent les courbes de pression de vapeur de diverses substances. Le fait que toutes les substances connues dans la région diphasique remplissent l’équation de Clausius-Clapeyronfournit la validité générale des 1ère et2ème lois de la thermodynamique !
Suivant : 8.5 Les cycles de puissance de Rankine Haut : 8. Cycles de puissance avec Précédent : 8.3 Le cycle de Carnot Sommaire Index
UnifiedTP