Un algorithme diviser et conquérir est une stratégie de résolution d’un grand problème en
- brisant le problème en sous-problèmes plus petits
- résolvant les sous-problèmes, et
- les combinant pour obtenir le résultat souhaité.
Pour utiliser l’algorithme diviser et conquérir, la récursion est utilisée. Découvrez la récursion dans différents langages de programmation :
- Récursion en Java
- Récursion en Python
- Récursion en C++
Comment fonctionnent les algorithmes de division et de conquête ?
Voici les étapes impliquées :
- Diviser : Diviser le problème donné en sous-problèmes en utilisant la récursion.
- Conquérir : Résoudre les plus petits sous-problèmes de manière récursive. Si le sous-problème est suffisamment petit, alors le résoudre directement.
- Combiner : Combiner les solutions des sous-problèmes qui font partie du processus récursif pour résoudre le problème réel.
Comprenons ce concept à l’aide d’un exemple.
Ici, nous allons trier un tableau en utilisant l’approche diviser et conquérir (ie. merge sort).
- Disons que le tableau donné est :

Tableau pour le merge sort - Diviser le tableau en deux moitiés.
Diviser le tableau en deux sous-parties Encore, diviser chaque sous-partie récursivement en deux moitiés jusqu’à obtenir des éléments individuels.
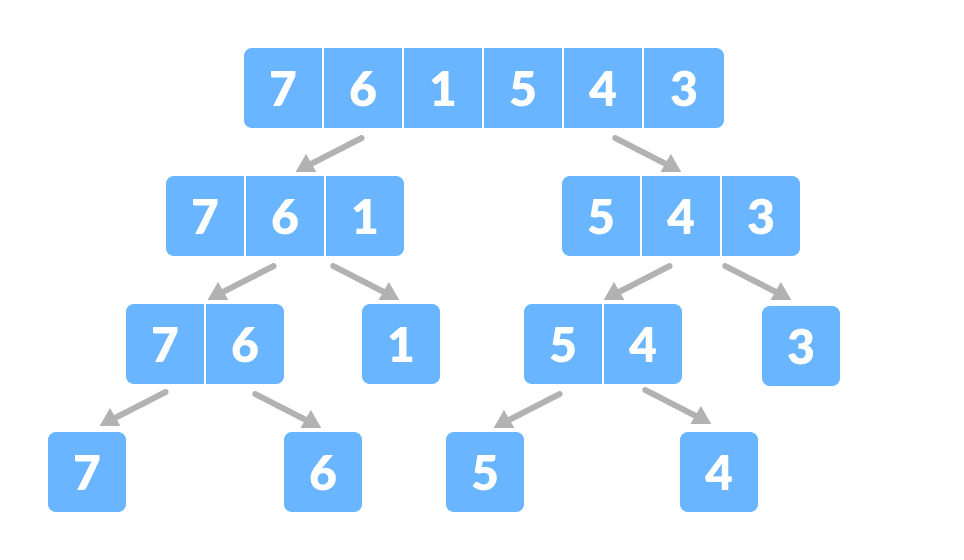
Diviser le tableau en sous-parties plus petites - Maintenant, combinez les éléments individuels de manière triée. Ici, les étapes de conquête et de combinaison vont côte à côte.
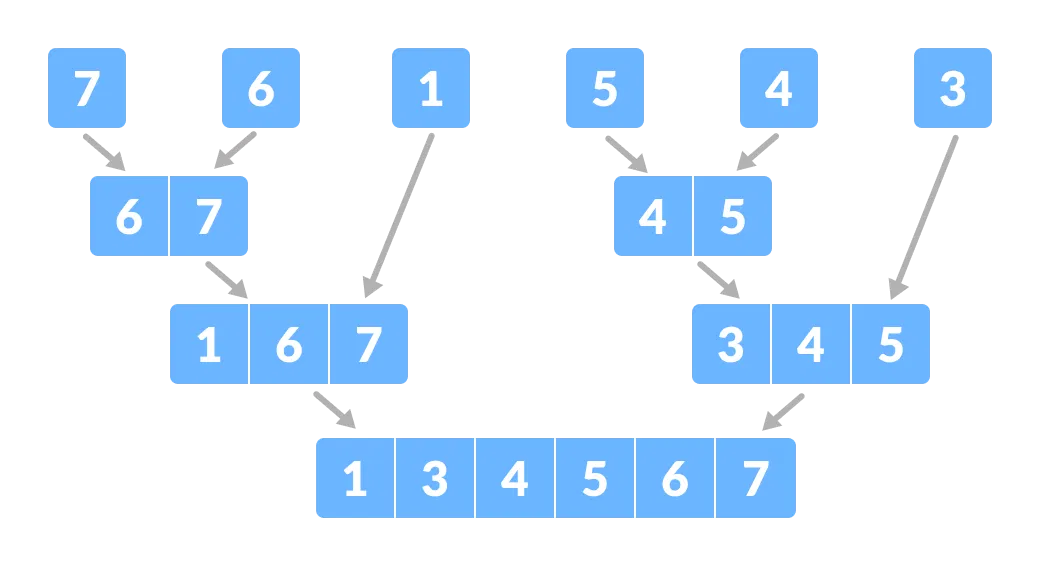
Combiner les sous-parties .
Complexité temporelle
La complexité de l’algorithme diviser pour régner est calculée à l’aide du théorème du maître.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Prenons un exemple pour trouver la complexité temporelle d’un problème récursif.
Pour un tri par fusion, l’équation peut être écrite comme suit :
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Diviser et conquérir Vs approche dynamique
L’approche diviser et conquérir divise un problème en sous-problèmes plus petits ; ces sous-problèmes sont ensuite résolus de manière récursive. Le résultat de chaque sous-problème n’est pas stocké pour référence future, alors que, dans une approche dynamique, le résultat de chaque sous-problème est stocké pour référence future.
Utilisez l’approche diviser et conquérir lorsque le même sous-problème n’est pas résolu plusieurs fois. Utilisez l’approche dynamique lorsque le résultat d’un sous-problème doit être utilisé plusieurs fois dans le futur.
Permettons de comprendre cela avec un exemple. Supposons que nous essayons de trouver la série de Fibonacci. Alors,
Approche Diviser et Conquérir:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Approche dynamique:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
Dans une approche dynamique, mem stocke le résultat de chaque sous-problème.
Avantages de l’algorithme diviser et conquérir
- La complexité pour la multiplication de deux matrices en utilisant la méthode naïve est O(n3), alors qu’en utilisant l’approche diviser et conquérir (c’est-à-dire la multiplication de matrice de Strassen) est O(n2,8074). Cette approche simplifie également d’autres problèmes, comme la tour de Hanoi.
- Cette approche est adaptée aux systèmes multiprocesseurs.
- Elle utilise efficacement les caches mémoire.
Applications de division et de conquête
- Recherche binaire
- Tri de fusion
- Tri rapide
- Multiplication matricielle de Strassen
- Algorithme de Karatsuba
.


