Débat sur les fluides Table des matières
Connaissances en hydraulique et pneumatique
Équipement de puissance des fluides
La chute de pression dans les tuyaux est causée par :
- Frottement
- Différence ou élévation verticale des tuyaux
- Changements d’énergie cinétique
- Calcul de la chute de pression causée par le frottement dans les tuyaux circulaires
Pour déterminer la chute de pression du fluide (liquide ou gaz) le long d’un tuyau ou d’un élément de tuyau, il faut effectuer les calculs suivants, dans l’ordre suivant .
Equation du nombre de Reynolds :
|
Re = ω D / v Re = ρ v l / µ Re = ω l / v |
Où : Re = Nombre de Reynolds (sans unité) Viscosité cinématique Exemple de valeurs de viscosité cinématique pour l’air et l’eau à 1 atm et à différentes températures. Viscosité cinématique de l’air m2/a
Viscosité cinématique de l’eau m2/ a
Tableau de viscosité cinématique. Tableau des liquides |
Si le nombre de Reynolds < 2320, alors vous avez un écoulement laminaire.
L’écoulement laminaire se caractérise par le glissement de couches cylindriques concentriques les unes à côté des autres de manière ordonnée. La vitesse du fluide est maximale à l’axe du tuyau et diminue fortement pour devenir nulle à la paroi. La perte de charge due au frottement de l’écoulement laminaire ne dépend pas de la rugosité du tuyau.
Si le nombre de Reynolds > 2320, on a un écoulement turbulent.
Il y a un mouvement irrégulier des particules de fluide dans des directions transversales à la direction de l’écoulement principal. La distribution de la vitesse d’un écoulement turbulent est plus uniforme sur le diamètre du tuyau que dans un écoulement laminaire. La chute de pression causée par la friction de l’écoulement turbulent dépend de la rugosité du tuyau.
Sélectionner le coefficient de frottement du tuyau :
Le coefficient de frottement du tuyau est un nombre sans dimension. Le coefficient de frottement pour une condition d’écoulement laminaire est fonction du nombre de Reynolds uniquement, pour un écoulement turbulent, il est également fonction des caractéristiques de la paroi du tuyau.
Déterminer le coefficient de frottement de la conduite à l’écoulement laminaire :
λ = 64 / Re
Où :
λ = coefficient de frottement de la conduite
Re = nombre de Reynolds
Note : les conduites parfaitement lisses auront une rugosité de zéro.
Déterminer le coefficient de friction de la tuyauterie lors d’un écoulement turbulent (dans la plupart des cas) Équation de Colbrook :
ou
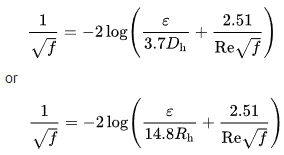
Où :
= Coefficient de friction du tuyau
g = Accélération de la gravité (9.8 m/s/s)
Re = Nombre de Reynolds (sans unité)
k = Rugosité absolue (mm)
D = Diamètre de la conduite (m)
lg = Court pour Log
Les solutions de ce calcul sont tracées en fonction du nombre de Reynolds pour créer un graphique de Moody.
Le tableau suivant donne les valeurs de rugosité typiques en millimètres pour les matériaux de tuyauterie couramment utilisés.
| Matériau de surface |
Coefficient de rugosité absolue – k (mm)
|
Aluminium, plomb |
0.001 – 0,002
|
Laiton étiré, cuivre étiré |
0.0015
|
Aluminium, plomb |
0,001 – 0,002
|
PVC, tuyaux en plastique |
0.0015
|
| Fibre de verre |
0,005
|
Acier inoxydable |
0.015
|
Tuyau commercial en acier |
0,045 – 0.09
|
Acier trempé |
0,015
|
| Acier à souder |
0.045
|
| Acier galvanisé |
0,15
|
| Acier rouillé |
0.15 – 4
|
| Acier ruiné |
0,9 – 9
|
Fonte neuve |
0,25 – 0.8
|
Fonte usée |
0,8 – 1,5
|
Fonte corrodée |
1.5 – 2,5
|
Fonte asphaltée |
0.012
|
Fonte galvanisée |
0,015
|
Ciment lissé |
0.3
|
Béton ordinaire |
0,3 – 3
|
Bois bien raboté |
0,18 – 0.9
|
Bois ordinaire |
5
|
Déterminer la perte de charge dans des tuyaux circulaires :
Où :
Δp = Perte de charge (Pa ou kg / m-s 2)
λ = Coefficient de friction du tuyau
L = Longueur du tuyau (m)
D = Diamètre du tuyau (m)
p = Densité (kg/m3)
ω = Vitesse d’écoulement (m/s)
Si vous avez des vannes, coudes et d’autres éléments le long de votre tuyau, alors vous calculez la perte de charge avec des coefficients de résistance spécifiques à l’élément. Les coefficients de résistance sont dans la plupart des cas trouvés par des tests pratiques et par les documents de spécification des fournisseurs. Si le coefficient de résistance est connu, alors on peut calculer la perte de charge pour l’élément.
Où :
= Perte de charge (kg/m2)
= Coefficient de résistance (déterminé par un essai ou une spécification du fournisseur)
p = Densité (kg/m3)
ω = Vitesse d’écoulement
Chute de pression par gravité ou élévation verticale
Où :
Δp = Perte de charge (kg/m2)
p = Densité (kg/m3)
g = Accélération de la gravité (9,8 m/s/s)
ΔH = Élévation ou chute verticale(m)
La perte de charge des gaz et des vapeurs
Les fluides compressibles se dilatent sous l’effet des pertes de charge (frottement) et la vitesse augmente. Par conséquent est la chute de pression le long du tuyau n’est pas constante.
Où :
p1 = Pression entrante (kg/m2)
T1 = Température entrante (°C)
p2 = Pression sortante (kg/m2)
T2 = Température sortante (°C)
Nous fixons le nombre de friction de la conduite comme une constante et le calculons avec les données d’entrée. La température, qui est utilisée dans l’équation, est la moyenne de l’entrée et de la sortie du tuyau.
Note : Vous pouvez calculer les gaz comme des liquides, si le changement relatif de densité est faible (changement de densité/densité = 0,02).