Heading

Just another blog

Distribution binomiale

Contributeurs MathWorld > Yap >

Télécharger Mathematica NotebookEXPLOREZ CE SUJET DANS la classe MathWorldBinomialDistribution

La distribution binomiale donne la distribution de probabilité discrète P_p(n|N) d’obtenir exactement n succès sur N. essais de Bernoulli (où le résultat de chaque essai de Bernoulli est vrai avec la probabilité p et faux avec la probabilité q=1-p). La distribution binomiale est donc donnée par

.P_p(n|N)P_p(n|N)
 = (N ; n)p^nq^(N-n)
(1)
= (N !)/(n !(N-n) !)p^n(1-p)^(N-n),
(2)

où (N ; n) est un coefficient binomial. Le graphique ci-dessus montre la distribution de n succès sur N=20 essais avec p=q=1/2.

La distribution binomiale est implémentée dans le langage Wolfram sous la forme BinomialDistribution.

La probabilité d’obtenir plus de succès que le n observé dans une distribution binomiale est

P=somme_(k=n+1)^N(N ; k)p^k(1-p)^(N-k)=I_p(n+1,N-n),
(3)

où

I_x(a,b)=(B(x ;a,b))/(B(a,b)),
(4)

B(a,b) est la fonction bêta, et B(x ;a,b) est la fonction bêta incomplète.

La fonction caractéristique de la distribution binomiale est

. phi(t)=(q+pe^(it))^N
(5)

(Papoulis 1984, p. 154). La fonction génératrice de momentsgénératrice M pour la distribution est

M(t) = e^(tn)
(6)
= somme_(n=0)^(N)e^(tn)(N ; n)p^nq^(N-n)
(7)
= somme_(n=0)^(N)(N ; n)(pe^t)^n(1-p)^(N-n)
(8)
= ^N
(9)
M^'(t)'(t) = N^(N-1)(pe^t)N^(N-1)(pe^t)
(10)
M^('')(t)'')(t) = N(N-1)^(N-2)(pe^t)^2+N^(N-1)(pe^t).
(11)

La moyenne est

.

mu = M^'(0)'(0)
(12)
= N(p+1-p)p
(13)
= Np.
(14)

Les moments autour de 0 sont

.

mu_1^'' = mu=Np
(15)
mu_2^'' = Np(1-p+Np)
(16)
mu_3^'' = Np(1-3p+3Np+2p^2-3Np^2+N^2p^2)
(17)
mu_4^'' = Np(1-7p+7Np+12p^2-18Np^2+6N^2p^2-6p^3+11Np^3-6N^2p^3+N^3p^3),
(18)

donc les moments autour de la moyenne sont

mu_2 = Np(1-p)=NpqNp(1-p)=Npq
(19)
mu_3 = Np(1-p)(1-2p)
(20)
mu_4 = Np(1-p).
(21)

L’asymétrie et l’aplatissement sont

gamma_1 = (1-2p)/(sqrt(Np(1-p)))
(22)
= (q-p)/(sqrt(Npq))
(23)
gamma_2 = (6p^2-6p+1)/(Np(1-p))
(24)
= (1-6pq)/(Npq).
(25)

Le premier cumulant est

kappa_1=np,
(26)

et les cumulants subséquents sont donnés par la relation de récurrence

kappa_(r+1)=pq(dkappa_r)/(dp).
(27)

L’écart moyen est donné par

. écart moyen est donné par

MD=somme_(k=0)^N|k-Np|(N ; k)p^k(1-p)^(N-k).
(28)

Pour le cas particulier p=q=1/2, ceci est égal à

MD
 = 2^(-N)sum_(k=0)^(N)(N ; k)|k-1/2N|
(29)
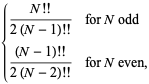= {(N !!)/(2(N-1) !!) pour N impair ; ((N-1) !!)/(2(N-2) !!!) pour N pair,
(30)

où N!! est une double factorielle. Pour N=1, 2, …, les premières valeurs sont donc 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, …. (OEIS A086116 et A086117). Le cas général est donné par

MD=2(1-p)^(N-|_Np_|)p^(|_Np_|+1)(|_Np_|+1)(N ; |_Np_|+1).
(31)

Steinhaus (1999, pp. 25-28) considère le nombre attendu de carrés S(n,N,s) contenant un nombre donné de grains n sur une planche de taille s après distribution aléatoire de N de grains,

S(n,N,s)=sP_(1/s)(n|N).
(32)

En prenant N=s=64 on obtient les résultats résumés dans le tableau suivant.

n S(n,64,64)
0 23.3591
1 23,7299
2 11,8650
3 3.89221
4 0,942162
5 0.179459
6 0,0280109
7 0.0036840
8 4,16639×10^(-4)
4.11495×10^(-5)
10 3.59242×10^(-6)

Une approximation de la distribution binomiale pour de grandes N peut être obtenue par expansion autour de la valeur n^~ où P(n) est un maximum, i.e., où dP/dn=0. Comme la fonction logarithme est monotone, on peut plutôt choisir de développer le logarithme. Soit n=n^~+eta, alors

ln=ln+B_1eta+1/2B_2eta^2+1/(3 !)B_3eta^3+....,
(33)

où

B_k=)/(dn^k)]_(n=n^~).
(34)

Mais nous sommes en expansion autour du maximum, donc, par définition,

B_1=)/(dn)]_(n=n^~)=0.
(35)

Cela signifie aussi que B_2 est négatif, on peut donc écrire B_2=-|B_2|. Maintenant, en prenant le logarithme de (◇) on obtient

ln=lnN!-lnn!-ln(N-n)!+nlnp+(N-n)lnq.
(36)

Pour les grandes n et N-n on peut utiliser l’approximation de Stirling

ln(n !) approx nlnn-n,
(37)

alors

(d)/(dn) approx (lnn+1)-1
(38)
= lnn
(39)
(d)/(dn) approx d/(dn)
(40)
=
(41)
= -ln(N-n),
(42)

et

(dln)/(dn) approx -lnn+ln(N-n)+lnp-lnq.
(43)

Pour trouver n^~, mettez cette expression à 0 et résolvez n,

ln((N-n^~)/(n^~)p/q)=0
(44)
(N-n^~)/(n^~)p/q=1
(45)
(N-n^~)p=n^~q (N-n^~)p=n^~q
(46)
n^~(q+p)=n^~=Np,
(47)

puisque p+q=1. Nous pouvons maintenant trouver les termes de l’expansion

B_2 =
)/(dn^2)]_(n=n^~)
(48)
= -1/(n^~)-1/(N-n^~)
(49)
= -1/(Npq)
(50)
= -1/(Np(1-p))
(51)
B_3 = )/(dn^3)]_(n=n^~)
(52)
= 1/(n^~^2)-1/((N-n^~)^2)
(53)
= (q^2-p^2)/(N^2p^2q^2)
(54)
= (1-2p)/(N^2p^2(1-p)^2)
(55)
B_4 = )/(dn^4)]_(n=n^~)
(56)
= -2/(n^~^3)-2/((n-n^~)^3)
(57)
= (2(p^2-pq+q^2))/(N^3p^3q^3)
(58)
= (2(3p^2-3p+1))/(N^3p^3(1-p)^3)).
(59)

BinomialGaussien

Maintenant, en traitant la distribution comme continue,

lim_(N-infty)sum_(n=0)^NP(n) approx intP(n)dn=int_(-infty)^inftyP(n^~+eta)deta=1.
(60)

Si chaque terme est d’ordre 1/N∼1/sigma^2 plus petit que le précédent, nous pouvons ignorer les termes supérieurs à B_2, donc

P(n)=P(n^~)e^(-|B_2|eta^2/2).
(61)

La probabilité doit être normalisée, donc

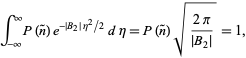int_(-infty)^inftyP(n^~)e^(-|B_2|eta^2/2)deta=P(n^~)sqrt((2pi)/(|B_2|))=1,
(62)

et

P(n) = sqrt((|B_2|)/(2pi))e^(-|B_2|(n-n^~)^2/2)
(63)
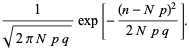= 1/(sqrt(2piNpq))exp.
(64)

Définir sigma^2=Npq,

P(n)=1/(sigmasqrt(2pi))exp,
(65)

qui est une distribution normale. La distribution binomiale est donc approximée par une distribution normale pour tout p fixé (même si p est petit) car N est pris à l’infini.

Si N-infty et p-0 de telle sorte que Np-lambda, alors la distribution binomiale converge vers la distribution de Poisson de moyenne lambda.

Détendons que x et y sont des variables aléatoires binomiales indépendantes caractérisées par les paramètres n,p et m,p. La probabilité conditionnelle de x étant donné que x+y=k est

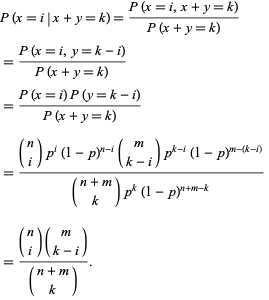P(x=i|x+y=k)=(P(x=i,x+y=k))/(P(x+y=k)) =(P(x=i,y=k-i))/(P(x+y=k)) =(P(x=i)P(y=k-i))/(P(x+y=k)) =((n ; i)p^i(1-p)^(n-i)(m ; k-i)p^(k-i)(1-p)^(m-(k-i)))/((n+m ; k)p^k(1-p)^(n+m-k)) =((n ; i)(m ; k-i))/((n+m ; k)).
(66)

Notez que ceci est une distribution hypergéométrique.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *