Retourner à l’index des leçons | Faire les leçons dans l’ordre | Page imprimable
Factorielles
Les factorielles sont des choses très simples. Ce sont juste des produits, indiqués par un point d’exclamation. Par exemple, la » factorielle à quatre » s’écrit » 4 ! » et signifie 1×2×3×4 = 24. En général, n ! ( » enn factorielle « ) désigne le produit de tous les nombres entiers de 1 à n ; c’est-à-dire n ! = 1×2×3×…×n.
(Pour diverses raisons, 0 ! est défini comme étant égal à 1, et non à 0. Mémorisez ceci maintenant : 0 ! = 1.)
- Évaluez 6 !.
1×2×3×4×5×6 = 720
De nombreuses (la plupart ?) calculatrices peuvent évaluer les factorielles pour vous. Par exemple, la commande factorielle est disponible dans le menu « probabilité » d’une de mes calculatrices :

Recherchez un bouton » ! « , ou consultez votre manuel d’utilisation.
- Simplifiez 12 ! Copyright © Elizabeth Stapel 2004-2011 Tous droits réservés
12 ! = 1×2×3×4×… Oh, au diable tout ça. Où est ma calculatrice…?

12 ! = 479001600
Promotion
Lorsque vous commencerez à faire des combinaisons, des permutations et des probabilités, vous devrez simplifier des expressions qui ont des factorielles dans les numérateurs et les dénominateurs. Par exemple :
- Simplifiez les expressions suivantes :
![]()
Je peux le faire dans ma calculatrice:

Je peux aussi travailler à partir de la définition d’une factorielle :
![]()
Dans les deux cas, 6 ! ÷ 4 ! = 30
Notez comment j’ai pu annuler un tas de chiffres dans le problème précédent. Cela est dû à la façon dont les factorielles sont définies, et cette propriété peut beaucoup simplifier votre travail.
- Simplifiez ce qui suit :
![]()
D’emblée, je peux annuler les facteurs 1 à 14 qui seront communs à 17 ! et 14 !. Je peux ensuite simplifier ce qui reste pour obtenir :
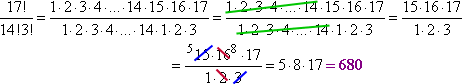
Voyez comment j’ai raccourci ce que j’avais à écrire en laissant un vide (l' » ellipse « , ou triple point) au milieu. Ce procédé d’écart et d’annulation deviendra pratique plus tard (comme en calcul, où vous utiliserez beaucoup cette technique), notamment lorsque vous aurez affaire à des expressions que votre calculatrice ne peut pas gérer. Par exemple :
- Simplifiez ce qui suit :
![]()
Ma calculatrice ne peut pas évaluer cela pour moi, puisque je traite des variables plutôt que des nombres. Je vais devoir simplifier cela à la main. Pour ce faire, je vais écrire les factorielles, en utilisant suffisamment de facteurs pour avoir des choses qui peuvent s’annuler. En repensant aux problèmes de mots » nombres « , les nombres entiers consécutifs sont séparés d’une unité, donc les facteurs du produit (n + 2) ! sont de la forme :
1×2×3×4×….×(n – 1)×(n)×(n + 1)×(n + 2)
En remontant la liste des facteurs jusqu’à » n – 1 « , j’ai créé une liste de facteurs qui peuvent s’annuler :
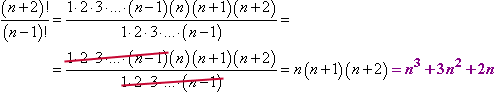
Notez la façon dont j’ai traité cette annulation. J’ai développé les expressions factorielles suffisamment pour que je puisse voir où je pouvais annuler les facteurs en double. Même si je n’avais aucune idée de ce que n pouvait être, je pouvais quand même annuler. Rangez cette technique dans votre cerveau, car même si vous n’en avez pas besoin maintenant, vous en aurez presque certainement besoin plus tard.
Pour des informations sur la recherche du nombre de zéros à la fin d’une factorielle (comme « Combien de zéros y a-t-il à la fin de 23 ! après l’avoir multiplié ? »), consultez cette note.
Haut | Retour à l’index
|
Citer cet article comme: |
Stapel, Elizabeth. « Factorielles. » Purplemath. Disponible à partir de 2016
|
.