Heading

L’intérêt pour l’apprentissage automatique est monté en flèche au cours des années depuis que l’article de Harvard Business Review a désigné le  » Data Scientist  » comme le  » job le plus sexy du 21e siècle « . Mais si vous débutez dans l’apprentissage automatique, il peut être un peu difficile de percer. C’est pourquoi nous redémarrons notre post immensément populaire sur les bons algorithmes d’apprentissage automatique pour les débutants.

(Ce post a été initialement publié sur KDNuggets sous le titre Les 10 algorithmes que les ingénieurs en apprentissage automatique doivent connaître. Il a été reposté avec autorisation, et a été mis à jour pour la dernière fois en 2019).

Ce billet s’adresse aux débutants. Si vous avez une certaine expérience de la science des données et de l’apprentissage automatique, vous serez peut-être plus intéressé par ce tutoriel plus approfondi sur la réalisation de l’apprentissage automatique en Python avec scikit-learn, ou par nos cours d’apprentissage automatique, qui commencent ici. Si vous n’êtes pas encore au clair sur les différences entre la  » science des données  » et l' » apprentissage automatique « , cet article offre une bonne explication : apprentissage automatique et science des données – ce qui les différencie ?

Les algorithmes d’apprentissage automatique sont des programmes capables d’apprendre à partir de données et de s’améliorer grâce à l’expérience, sans intervention humaine. Les tâches d’apprentissage peuvent inclure l’apprentissage de la fonction qui fait correspondre l’entrée à la sortie, l’apprentissage de la structure cachée dans les données non étiquetées ; ou encore l' » apprentissage basé sur les instances « , où une étiquette de classe est produite pour une nouvelle instance en comparant la nouvelle instance (ligne) aux instances des données d’apprentissage, qui ont été stockées en mémoire. L' » apprentissage basé sur les instances  » ne crée pas d’abstraction à partir d’instances spécifiques.

Types d’algorithmes d’apprentissage automatique

Il existe 3 types d’algorithmes d’apprentissage automatique (IA) :

Agorithmes d’apprentissage supervisé :

L’apprentissage supervisé utilise des données d’apprentissage étiquetées pour apprendre la fonction de mappage qui transforme les variables d’entrée (X) en variable de sortie (Y). En d’autres termes, il résout f dans l’équation suivante :

Y = f (X)

Cela nous permet de générer avec précision des sorties lorsqu’on nous donne de nouvelles entrées.

Nous allons parler de deux types d’apprentissage supervisé : la classification et la régression.

La classification est utilisée pour prédire le résultat d’un échantillon donné lorsque la variable de sortie se présente sous la forme de catégories. Un modèle de classification pourrait examiner les données d’entrée et essayer de prédire des étiquettes telles que « malade » ou « en bonne santé ».

La régression est utilisée pour prédire le résultat d’un échantillon donné lorsque la variable de sortie se présente sous la forme de valeurs réelles. Par exemple, un modèle de régression pourrait traiter les données d’entrée pour prédire la quantité de pluie, la taille d’une personne, etc.

Les 5 premiers algorithmes que nous couvrons dans ce blog – Régression linéaire, Régression logistique, CART, Naïve-Bayes et K-Nearest Neighbors (KNN) – sont des exemples d’apprentissage supervisé.

L’assemblage est un autre type d’apprentissage supervisé. Il consiste à combiner les prédictions de plusieurs modèles d’apprentissage automatique qui sont individuellement faibles pour produire une prédiction plus précise sur un nouvel échantillon. Les algorithmes 9 et 10 de cet article – Bagging avec Random Forests, Boosting avec XGBoost – sont des exemples de techniques d’ensemble.

Argorithmes d’apprentissage non supervisé :

Les modèles d’apprentissage non supervisé sont utilisés lorsque nous n’avons que les variables d’entrée (X) et aucune variable de sortie correspondante. Ils utilisent des données d’entraînement non étiquetées pour modéliser la structure sous-jacente des données.

Nous allons parler de trois types d’apprentissage non supervisé :

L’association est utilisée pour découvrir la probabilité de la cooccurrence d’éléments dans une collection. Elle est très utilisée dans l’analyse des paniers de marché. Par exemple, un modèle d’association peut être utilisé pour découvrir que si un client achète du pain, il a 80 % de chances d’acheter également des œufs.

La clusterisation est utilisée pour regrouper des échantillons de sorte que les objets d’un même cluster soient plus similaires entre eux qu’aux objets d’un autre cluster.

La réduction de la dimensionnalité est utilisée pour réduire le nombre de variables d’un ensemble de données tout en s’assurant que les informations importantes sont toujours transmises. La réduction de la dimensionnalité peut être effectuée à l’aide de méthodes d’extraction de caractéristiques et de méthodes de sélection de caractéristiques. La sélection des caractéristiques permet de sélectionner un sous-ensemble des variables originales. L’extraction de caractéristiques permet de transformer les données d’un espace à haute dimension en un espace à basse dimension. Exemple : L’algorithme PCA est une approche d’Extraction de caractéristiques.

Les algorithmes 6-8 que nous couvrons ici – Apriori, K-means, PCA – sont des exemples d’apprentissage non supervisé.

Apprentissage par renforcement :

L’apprentissage par renforcement est un type d’algorithme d’apprentissage automatique qui permet à un agent de décider de la meilleure action suivante en fonction de son état actuel en apprenant les comportements qui maximiseront une récompense.

Les algorithmes de renforcement apprennent généralement les actions optimales par essais et erreurs. Imaginez, par exemple, un jeu vidéo dans lequel le joueur doit se déplacer à certains endroits à certains moments pour gagner des points. Un algorithme de renforcement jouant à ce jeu commencerait par se déplacer de manière aléatoire mais, au fil du temps, par essais et erreurs, il apprendrait où et quand il doit déplacer le personnage du jeu pour maximiser son total de points.

Quantifier la popularité des algorithmes d’apprentissage automatique

Où avons-nous trouvé ces dix algorithmes ? Toute liste de ce type sera intrinsèquement subjective. Des études comme celles-ci ont quantifié les 10 algorithmes d’exploration de données les plus populaires, mais elles s’appuient toujours sur les réponses subjectives des personnes interrogées, généralement des praticiens universitaires avancés. Par exemple, dans l’étude liée ci-dessus, les personnes interrogées étaient les lauréats du prix de l’innovation ACM KDD, du prix des contributions à la recherche IEEE ICDM ; les membres du comité de programme des KDD ’06, ICDM ’06, et SDM ’06 ; et les 145 participants de l’ICDM ’06.

Les 10 meilleurs algorithmes énumérés dans ce post sont choisis en pensant aux débutants en apprentissage automatique. Ce sont principalement des algorithmes que j’ai appris dans le cours  » Data Warehousing and Mining  » (DWM) pendant ma licence en ingénierie informatique à l’Université de Mumbai. J’ai inclus les 2 derniers algorithmes (méthodes d’ensemble) notamment parce qu’ils sont fréquemment utilisés pour gagner les compétitions Kaggle.

Sans plus attendre, les 10 meilleurs algorithmes d’apprentissage automatique pour les débutants :

1. Régression linéaire

En apprentissage automatique, nous avons un ensemble de variables d’entrée (x) qui sont utilisées pour déterminer une variable de sortie (y). Une relation existe entre les variables d’entrée et la variable de sortie. Le but de l’apprentissage automatique est de quantifier cette relation.

Figure 1 : La régression linéaire est représentée par une ligne de la forme y = a + bx. Source

Dans la régression linéaire, la relation entre les variables d’entrée (x) et la variable de sortie (y) est exprimée par une équation de la forme y = a + bx. Ainsi, le but de la régression linéaire est de trouver les valeurs des coefficients a et b. Ici, a est l’intercept et b est la pente de la ligne.

La figure 1 montre les valeurs x et y tracées pour un ensemble de données. L’objectif est d’ajuster une ligne qui est la plus proche de la plupart des points. Cela permettrait de réduire la distance ( » erreur « ) entre la valeur y d’un point de données et la ligne.

2. Régression logistique

Les prédictions de la régression linéaire sont des valeurs continues (par exemple, les précipitations en cm), les prédictions de la régression logistique sont des valeurs discrètes (par exemple, si un étudiant a réussi/échoué) après application d’une fonction de transformation.

La régression logistique est plus adaptée à la classification binaire : des ensembles de données où y = 0 ou 1, où 1 désigne la classe par défaut. Par exemple, pour prédire si un événement va se produire ou non, il n’y a que deux possibilités : qu’il se produise (que nous désignons par 1) ou qu’il ne se produise pas (0). Ainsi, si nous devions prédire si un patient est malade, nous étiquetterions les patients malades à l’aide de la valeur de 1 dans notre ensemble de données.

La régression logistique doit son nom à la fonction de transformation qu’elle utilise, appelée fonction logistique h(x)= 1/ (1 + ex). Cela forme une courbe en forme de S.

Dans la régression logistique, la sortie prend la forme de probabilités de la classe par défaut (contrairement à la régression linéaire, où la sortie est directement produite). Comme il s’agit d’une probabilité, la sortie se situe dans l’intervalle de 0 à 1. Ainsi, par exemple, si nous essayons de prédire si les patients sont malades, nous savons déjà que les patients malades sont désignés par 1, donc si notre algorithme attribue le score de 0,98 à un patient, il pense que ce patient est tout à fait susceptible d’être malade.

Cette sortie (valeur y) est générée par la transformation logarithmique de la valeur x, en utilisant la fonction logistique h(x)= 1/ (1 + e^ -x) . Un seuil est ensuite appliqué pour forcer cette probabilité dans une classification binaire.

Figure 2 : Régression logistique pour déterminer si une tumeur est maligne ou bénigne. Classée comme maligne si la probabilité h(x)>= 0,5. Source

Dans la figure 2, pour déterminer si une tumeur est maligne ou non, la variable par défaut est y = 1 (tumeur = maligne). La variable x pourrait être une mesure de la tumeur, telle que la taille de la tumeur. Comme le montre la figure, la fonction logistique transforme la valeur x des différentes instances de l’ensemble de données, dans une fourchette de 0 à 1. Si la probabilité franchit le seuil de 0,5 (indiqué par la ligne horizontale), la tumeur est classée comme maligne.

L’équation de régression logistique P(x) = e ^ (b0 +b1x) / (1 + e(b0 + b1x)) peut être transformée en ln(p(x) / 1-p(x)) = b0 + b1x.

Le but de la régression logistique est d’utiliser les données d’apprentissage pour trouver les valeurs des coefficients b0 et b1 telles qu’elles minimisent l’erreur entre le résultat prédit et le résultat réel. Ces coefficients sont estimés à l’aide de la technique d’estimation du maximum de vraisemblance.

3. CART

Les arbres de classification et de régression (CART) sont une mise en œuvre des arbres décisionnels.

Les nœuds non terminaux des arbres de classification et de régression sont le nœud racine et le nœud interne. Les nœuds terminaux sont les nœuds feuilles. Chaque nœud non terminal représente une seule variable d’entrée (x) et un point de fractionnement sur cette variable ; les nœuds feuilles représentent la variable de sortie (y). Le modèle est utilisé comme suit pour faire des prédictions : parcourir les splits de l’arbre pour arriver à un nœud feuille et sortir la valeur présente au nœud feuille.

L’arbre de décision de la figure 3 ci-dessous classe si une personne achètera une voiture de sport ou un minivan en fonction de son âge et de son statut marital. Si la personne a plus de 30 ans et n’est pas mariée, nous parcourons l’arbre comme suit : ‘plus de 30 ans ?’ -> oui -> ‘mariée ?’ -> non. Par conséquent, le modèle produit une voiture de sport.

Figure 3 : Parties d’un arbre de décision. Source

4. Bayes naïf

Pour calculer la probabilité qu’un événement se produise, étant donné qu’un autre événement s’est déjà produit, on utilise le théorème de Bayes. Pour calculer la probabilité que l’hypothèse(h) soit vraie, étant donné nos connaissances préalables(d), nous utilisons le théorème de Bayes comme suit :

P(h|d)= (P(d|h) P(h)) / P(d)

où:

• P(h|d) = Probabilité postérieure. La probabilité que l’hypothèse h soit vraie, étant donné les données d, où P(h|d)= P(d1| h) P(d2| h)….P(dn| h) P(d)
• P(d|h) = Vraisemblance. La probabilité de la donnée d étant donné que l’hypothèse h était vraie.
• P(h) = Probabilité préalable de classe. La probabilité que l’hypothèse h soit vraie (indépendamment des données)
• P(d) = Probabilité préalable du prédicteur. Probabilité des données (indépendamment de l’hypothèse)

Cet algorithme est appelé  » naïf  » car il suppose que toutes les variables sont indépendantes les unes des autres, ce qui est une hypothèse naïve à faire dans des exemples du monde réel.

Figure 4 : Utilisation de Naive Bayes pour prédire l’état de ‘play’ en utilisant la variable ‘weather’.

En utilisant la figure 4 comme exemple, quel est le résultat si météo = ‘ensoleillé’ ?

Pour déterminer l’issue play = ‘oui’ ou ‘non’ étant donné la valeur de la variable weather = ‘sunny’, calculez P(yes|sunny) et P(no|sunny) et choisissez l’issue ayant la plus grande probabilité.

->P(yes|sunny)= (P(sunny|yes) * P(yes)) / P(ensoleillé) = (3/9 * 9/14 ) / (5/14) = 0,60

-> P(no|ensoleillé)= (P(ensoleillé|non) * P(non)). / P(ensoleillé) = (2/5 * 5/14 ) / (5/14) = 0,40

Donc, si la météo =  » ensoleillé « , l’issue est jeu =  » oui « .

5. KNN

L’algorithme K-Nearest Neighbors utilise l’ensemble des données comme ensemble d’apprentissage, plutôt que de diviser l’ensemble de données en un ensemble d’apprentissage et un ensemble de test.

Lorsqu’un résultat est requis pour une nouvelle instance de données, l’algorithme KNN parcourt l’ensemble des données pour trouver les k instances les plus proches de la nouvelle instance, ou le nombre k d’instances les plus similaires au nouvel enregistrement, puis sort la moyenne des résultats (pour un problème de régression) ou le mode (classe la plus fréquente) pour un problème de classification. La valeur de k est spécifiée par l’utilisateur.

La similarité entre les instances est calculée à l’aide de mesures telles que la distance euclidienne et la distance de Hamming.

Algorithmes d’apprentissage non supervisé

6. Apriori

L’algorithme Apriori est utilisé dans une base de données transactionnelle pour extraire des ensembles d’articles fréquents et ensuite générer des règles d’association. Il est populairement utilisé dans l’analyse du panier de la ménagère, où l’on vérifie les combinaisons de produits qui cooccurrent fréquemment dans la base de données. En général, nous écrivons la règle d’association pour « si une personne achète l’article X, alors elle achète l’article Y » comme suit : X -> Y.

Exemple : si une personne achète du lait et du sucre, alors elle est susceptible d’acheter du café en poudre. Cela pourrait être écrit sous la forme d’une règle d’association comme : {lait,sucre} -> café en poudre. Les règles d’association sont générées après avoir franchi le seuil de soutien et de confiance.

Figure 5 : Formules de soutien, de confiance et de levée pour la règle d’association X->Y.

La mesure de support permet d’élaguer le nombre d’ensembles d’items candidats à considérer lors de la génération d’ensembles d’items fréquents. Cette mesure de support est guidée par le principe d’Apriori. Le principe d’Apriori stipule que si un ensemble d’items est fréquent, alors tous ses sous-ensembles doivent également être fréquents.

7. K-means

K-means est un algorithme itératif qui regroupe les données similaires en clusters.Il calcule les centroïdes de k clusters et affecte un point de données à ce cluster ayant la plus petite distance entre son centroïde et le point de données.

Figure 6 : Étapes de l’algorithme K-means. Source

Voici comment cela fonctionne :

Nous commençons par choisir une valeur de k. Ici, disons que k = 3. Ensuite, nous attribuons aléatoirement chaque point de données à l’un des 3 clusters. Calculer le centroïde de cluster pour chacun des clusters. Les étoiles rouges, bleues et vertes dénotent les centroïdes pour chacun des 3 clusters.

Puis, réassignez chaque point au centroïde de cluster le plus proche. Dans la figure ci-dessus, les 5 points supérieurs ont été assignés au cluster avec le centroïde bleu. Suivez la même procédure pour affecter les points aux clusters contenant les centroïdes rouges et verts.

Puis, calculez les centroïdes des nouveaux clusters. Les anciens centroïdes sont les étoiles grises ; les nouveaux centroïdes sont les étoiles rouges, vertes et bleues.

Enfin, répétez les étapes 2-3 jusqu’à ce qu’il n’y ait pas de basculement de points d’un cluster à l’autre. Une fois qu’il n’y a pas de commutation pendant 2 étapes consécutives, quittez l’algorithme K-means.

8. ACP

L’analyse en composantes principales (ACP) est utilisée pour rendre les données faciles à explorer et à visualiser en réduisant le nombre de variables. Cela se fait en capturant la variance maximale des données dans un nouveau système de coordonnées avec des axes appelés  » composantes principales « .

Chaque composante est une combinaison linéaire des variables d’origine et est orthogonale les unes aux autres. L’orthogonalité entre les composantes indique que la corrélation entre ces composantes est nulle.

La première composante principale capture la direction de la variabilité maximale dans les données. La deuxième composante principale capture le reste de la variance des données mais possède des variables non corrélées avec la première composante. De même, toutes les composantes principales successives (PC3, PC4 et ainsi de suite) capturent la variance restante tout en étant non corrélées avec la composante précédente.

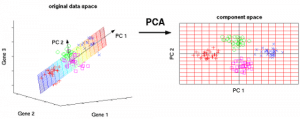
Figure 7 : Les 3 variables originales (gènes) sont réduites à 2 nouvelles variables appelées composantes principales (PC). Source

Techniques d’apprentissage par assemblage:

L’assemblage consiste à combiner les résultats de plusieurs apprenants (classificateurs) pour améliorer les résultats, par vote ou par moyenne. Le vote est utilisé lors de la classification et le calcul de la moyenne est utilisé lors de la régression. L’idée est que les ensembles d’apprenants donnent de meilleurs résultats que les apprenants uniques.

Il existe 3 types d’algorithmes d’assemblage : Bagging, Boosting et Stacking. Nous n’allons pas couvrir l' » empilement  » ici, mais si vous souhaitez une explication détaillée de celui-ci, voici une solide introduction de Kaggle.

9. Bagging avec Random Forests

La première étape du bagging consiste à créer plusieurs modèles avec des ensembles de données créés à l’aide de la méthode Bootstrap Sampling. Dans l’échantillonnage Bootstrap, chaque ensemble d’entraînement généré est composé de sous-échantillons aléatoires de l’ensemble de données original.

Chacun de ces ensembles d’entraînement est de la même taille que l’ensemble de données original, mais certains enregistrements se répètent plusieurs fois et d’autres n’apparaissent pas du tout. Ensuite, l’ensemble des données originales est utilisé comme ensemble de test. Ainsi, si la taille de l’ensemble de données d’origine est N, alors la taille de chaque ensemble d’entraînement généré est également N, le nombre d’enregistrements uniques étant d’environ (2N/3) ; la taille de l’ensemble de test est également N.

La deuxième étape du bagging consiste à créer plusieurs modèles en utilisant le même algorithme sur les différents ensembles d’entraînement générés.

C’est là que les forêts aléatoires entrent en jeu. Contrairement à un arbre de décision, où chaque nœud est divisé sur la meilleure caractéristique qui minimise l’erreur, dans les forêts aléatoires, nous choisissons une sélection aléatoire de caractéristiques pour construire la meilleure division. La raison de ce caractère aléatoire est la suivante : même avec la mise en sac, lorsque les arbres de décision choisissent la meilleure caractéristique sur laquelle se répartir, ils finissent par avoir une structure similaire et des prédictions corrélées. Mais la mise en sac après le fractionnement sur un sous-ensemble aléatoire de caractéristiques signifie moins de corrélation entre les prédictions des sous-arbres.

Le nombre de caractéristiques à rechercher à chaque point de fractionnement est spécifié comme un paramètre à l’algorithme Random Forest.

Ainsi, dans la mise en sac avec Random Forest, chaque arbre est construit à l’aide d’un échantillon aléatoire d’enregistrements et chaque fractionnement est construit à l’aide d’un échantillon aléatoire de prédicteurs.

10. Boosting avec AdaBoost

Adaboost est l’abréviation de Adaptive Boosting. Le bagging est un ensemble parallèle car chaque modèle est construit indépendamment. En revanche, le boosting est un ensemble séquentiel où chaque modèle est construit en fonction de la correction des erreurs de classification du modèle précédent.

Le balisage implique surtout un  » vote simple « , où chaque classificateur vote pour obtenir un résultat final – celui qui est déterminé par la majorité des modèles parallèles ; le boosting implique un  » vote pondéré « , où chaque classificateur vote pour obtenir un résultat final qui est déterminé par la majorité – mais les modèles séquentiels ont été construits en attribuant des poids plus importants aux instances mal classées des modèles précédents.

Figure 9 : Adaboost pour un arbre de décision. Source

Dans la figure 9, les étapes 1, 2, 3 impliquent un apprenant faible appelé souche de décision (un arbre de décision à 1 niveau effectuant une prédiction basée sur la valeur d’une seule caractéristique d’entrée ; un arbre de décision dont la racine est immédiatement connectée à ses feuilles).

Le processus de construction d’apprenants faibles se poursuit jusqu’à ce qu’un nombre défini par l’utilisateur d’apprenants faibles ait été construit ou jusqu’à ce qu’il n’y ait plus d’amélioration pendant la formation. L’étape 4 combine les 3 souches de décision des modèles précédents (et a donc 3 règles de division dans l’arbre de décision).

D’abord, commencer avec une souche d’arbre de décision pour prendre une décision sur une variable d’entrée.

La taille des points de données montre que nous avons appliqué des poids égaux pour les classer comme un cercle ou un triangle. La souche de décision a généré une ligne horizontale dans la moitié supérieure pour classer ces points. Nous pouvons voir qu’il y a deux cercles incorrectement prédits comme étant des triangles. Par conséquent, nous allons attribuer des poids plus élevés à ces deux cercles et appliquer une autre souche de décision.

Deuxièmement, passer à une autre souche d’arbre de décision pour prendre une décision sur une autre variable d’entrée.

Nous observons que la taille des deux cercles mal classés de l’étape précédente est plus grande que les points restants. Maintenant, la deuxième souche de décision va essayer de prédire ces deux cercles correctement.

En raison de l’attribution de poids plus élevés, ces deux cercles ont été correctement classés par la ligne verticale à gauche. Mais cela a maintenant entraîné une mauvaise classification des trois cercles en haut. Par conséquent, nous allons attribuer des poids plus élevés à ces trois cercles en haut et appliquer une autre souche de décision.

Troisièmement, former une autre souche d’arbre de décision pour prendre une décision sur une autre variable d’entrée.

Les trois cercles mal classés de l’étape précédente sont plus grands que le reste des points de données. Maintenant, une ligne verticale vers la droite a été générée pour classer les cercles et les triangles.

Quatrièmement, combiner les souches de décision.

Nous avons combiné les séparateurs des 3 modèles précédents et observons que la règle complexe de ce modèle classe correctement les points de données par rapport à n’importe lequel des apprenants faibles individuels.

Conclusion:

Pour récapituler, nous avons couvert certains des algorithmes d’apprentissage automatique les plus importants pour la science des données :

• 5 techniques d’apprentissage supervisé- Régression linéaire, Régression logistique, CART, Naïve Bayes, KNN.
• 3 techniques d’apprentissage non supervisé- Apriori, K-means, PCA.
• 2 techniques d’assemblage- Bagging avec Random Forests, Boosting avec XGBoost.

Note de l’éditeur : Cet article a été initialement posté sur KDNuggets, et a été reposté avec permission. L’auteur Reena Shaw est un développeur et un journaliste spécialisé dans la science des données.

.