⇐ Sujet précédent|Sujet suivant ⇒ Table des matières
Avant de réaliser une expérience, vous devez effectuer une analyse de puissance pour estimer le nombre d’observations dont vous avez besoin pour avoir une bonne chance de détecter l’effet recherché.
Introduction
Lorsque vous concevez une expérience, c’est une bonne idée d’estimer la taille de l’échantillon dont vous aurez besoin. C’est particulièrement vrai si vous proposez de faire quelque chose de douloureux pour les humains ou d’autres vertébrés, où il est particulièrement important de minimiser le nombre d’individus (sans que la taille de l’échantillon soit si petite que toute l’expérience soit une perte de temps et de souffrance), ou si vous prévoyez une expérience très longue ou coûteuse. Des méthodes ont été développées pour de nombreux tests statistiques afin d’estimer la taille d’échantillon nécessaire pour détecter un effet particulier, ou pour estimer la taille de l’effet qui peut être détecté avec une taille d’échantillon particulière.
Pour faire une analyse de puissance, vous devez spécifier une taille d’effet. Il s’agit de la taille de la différence entre votre hypothèse nulle et l’hypothèse alternative que vous espérez détecter. Pour la recherche biologique appliquée et clinique, il peut y avoir une taille d’effet très précise que vous voulez détecter. Par exemple, si vous testez un nouveau shampooing pour chiens, le service marketing de votre entreprise peut vous dire que la production de ce nouveau shampooing ne serait intéressante que s’il rendait le pelage des chiens au moins 25 % plus brillant, en moyenne. Ce serait votre taille d’effet, et vous l’utiliseriez pour décider combien de chiens vous devriez faire passer dans le réflectomètre canin.
Lorsque vous faites de la recherche biologique de base, vous ne savez souvent pas quelle différence vous recherchez, et la tentation peut être de simplement utiliser la plus grande taille d’échantillon que vous pouvez vous permettre, ou d’utiliser une taille d’échantillon similaire à d’autres recherches dans votre domaine. Vous devriez tout de même effectuer une analyse de puissance avant de réaliser l’expérience, juste pour avoir une idée du type d’effets que vous pourriez détecter. Par exemple, certains fous anti-vaccination ont proposé que le gouvernement américain mène une vaste étude sur les enfants vaccinés et non vaccinés afin de déterminer si les vaccins provoquent l’autisme. La taille de l’effet qui serait intéressante n’est pas claire : 10 % d’autisme en plus dans un groupe ? 50 % de plus ? deux fois plus ? Cependant, une analyse de puissance montre que même si l’étude incluait tous les enfants non vaccinés des États-Unis âgés de 3 à 6 ans et un nombre égal d’enfants vaccinés, il faudrait qu’il y ait 25 % d’autisme en plus dans un groupe pour avoir de fortes chances de voir une différence significative. Une étude plus plausible, portant sur 5 000 enfants non vaccinés et 5 000 enfants vaccinés, ne permettrait de détecter une différence significative avec une puissance élevée que s’il y avait trois fois plus d’autisme dans un groupe que dans l’autre. Parce qu’il est peu probable qu’il y ait une si grande différence d’autisme entre les enfants vaccinés et non vaccinés, et parce que le fait de ne pas trouver de relation avec une telle étude ne convaincrait pas les kooks anti-vaccination qu’il n’y a pas de relation (rien ne les convaincrait qu’il n’y a pas de relation – c’est ce qui fait d’eux des kooks), l’analyse de puissance vous dit qu’une étude aussi vaste et coûteuse ne vaudrait pas la peine.
Paramètres
Il y a quatre ou cinq nombres impliqués dans une analyse de puissance. Vous devez choisir les valeurs de chacun d’eux avant de faire l’analyse. Si vous n’avez pas de bonne raison d’utiliser une valeur particulière, vous pouvez essayer différentes valeurs et regarder l’effet sur la taille de l’échantillon.
Taille de l’effet
La taille de l’effet est l’écart minimum par rapport à l’hypothèse nulle que vous espérez détecter. Par exemple, si vous traitez des poules avec quelque chose qui, vous l’espérez, modifiera le rapport des sexes de leurs poussins, vous pourriez décider que le changement minimum de la proportion des sexes que vous recherchez est de 10%. Vous diriez alors que votre taille d’effet est de 10 %. Si vous testez quelque chose pour que les poules pondent plus d’œufs, la taille de l’effet pourrait être de 2 œufs par mois.
Occasionnellement, vous aurez une bonne raison économique ou clinique de choisir une taille d’effet particulière. Si vous testez un supplément d’alimentation pour poulets qui coûte 1,50 $ par mois, vous êtes seulement intéressé à savoir s’il produira plus de 1,50 $ d’œufs supplémentaires chaque mois ; savoir qu’un supplément produit 0,1 œuf supplémentaire par mois n’est pas une information utile pour vous, et vous n’avez pas besoin de concevoir votre expérience pour le savoir. Mais pour la plupart des recherches biologiques fondamentales, l’ampleur de l’effet n’est qu’un joli chiffre rond que vous avez sorti de votre chapeau. Disons que vous faites une analyse de puissance pour une étude sur une mutation dans une région promotrice, pour voir si elle affecte l’expression génétique. Quelle importance a le changement d’expression génétique que vous recherchez ? 10% ? 20% ? 50% ? C’est un chiffre assez arbitraire, mais il aura un effet considérable sur le nombre de souris transgéniques qui donneront leur chère petite vie pour votre science. Si vous n’avez pas de bonne raison de rechercher une taille d’effet particulière, vous pouvez l’admettre et dessiner un graphique avec la taille de l’échantillon en abscisse et la taille de l’effet en ordonnée. G*Power le fera pour vous.
Alpha
Alpha est le niveau de signification du test (la valeur P), la probabilité de rejeter l’hypothèse nulle même si elle est vraie (un faux positif). La valeur habituelle est alpha=0,05. Certains calculateurs de puissance utilisent le alpha unilatéral, ce qui prête à confusion, car le alpha bilatéral est beaucoup plus courant. Assurez-vous de savoir lequel vous utilisez.
Bêta ou puissance
Bêta, dans une analyse de puissance, est la probabilité d’accepter l’hypothèse nulle, même si elle est fausse (un faux négatif), lorsque la différence réelle est égale à la taille d’effet minimale. La puissance d’un test est la probabilité de rejeter l’hypothèse nulle (obtenir un résultat significatif) lorsque la différence réelle est égale à la taille d’effet minimale. La puissance est égale à 1-beta. Il n’existe pas de consensus clair sur la valeur à utiliser, il s’agit donc d’un autre chiffre que vous sortez de votre chapeau ; une puissance de 80 % (équivalente à un bêta de 20 %) est probablement la plus courante, tandis que certaines personnes utilisent 50 % ou 90 %. Le coût pour vous d’un faux négatif doit influencer votre choix de puissance ; si vous voulez vraiment, vraiment être sûr de détecter votre taille d’effet, vous voudrez utiliser une valeur plus élevée pour la puissance (bêta plus faible), ce qui se traduira par une taille d’échantillon plus grande. Certains calculateurs de puissance vous demandent d’entrer le bêta, tandis que d’autres demandent la puissance (1-bêta) ; soyez bien sûr de comprendre lequel vous devez utiliser.
Ecart-type
Pour les variables de mesure, vous avez également besoin d’une estimation de l’écart-type. Plus l’écart-type est grand, plus il est difficile de détecter une différence significative, vous aurez donc besoin d’une taille d’échantillon plus importante. Votre estimation de l’écart-type peut provenir d’expériences pilotes ou d’expériences similaires dans la littérature publiée. Il est peu probable que votre écart-type une fois l’expérience réalisée soit exactement le même, donc votre expérience sera en fait un peu plus ou moins puissante que ce que vous aviez prévu.
Pour les variables nominales, l’écart-type est une fonction simple de la taille de l’échantillon, donc vous n’avez pas besoin de l’estimer séparément.
Comment ça marche
Les détails d’une analyse de puissance sont différents pour différents tests statistiques, mais les concepts de base sont similaires ; ici, je vais utiliser le test binomial exact comme exemple. Imaginez que vous étudiez les fractures du poignet, et que votre hypothèse nulle est que la moitié des personnes qui se cassent un poignet se cassent le poignet droit, et l’autre moitié le poignet gauche. Vous décidez que la taille d’effet minimale est de 10 % ; si le pourcentage de personnes qui se cassent le poignet droit est de 60 % ou plus, ou de 40 % ou moins, vous voulez obtenir un résultat significatif du test binomial exact. Je ne sais pas pourquoi vous avez choisi 10%, mais c’est ce que vous utiliserez. Alpha est de 5%, comme d’habitude. Vous voulez que la puissance soit de 90 %, ce qui signifie que si le pourcentage de poignets droits cassés est vraiment de 40 % ou 60 %, vous voulez une taille d’échantillon qui donnera un résultat significatif (P<0,05) 90 % du temps, et un résultat non significatif (qui serait un faux négatif dans ce cas) seulement 10 % du temps.
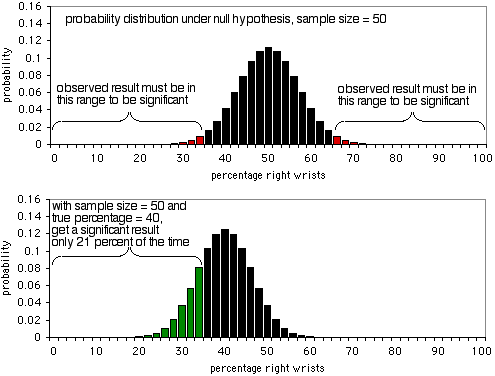

Le premier graphique montre la distribution de probabilité sous l’hypothèse nulle, avec une taille d’échantillon de 50 individus. Si l’hypothèse nulle est vraie, vous verrez moins de 36 % ou plus de 64 % de personnes se casser le poignet droit (un faux positif) environ 5 % du temps. Comme le montre le deuxième graphique, si le pourcentage réel est de 40 %, les données de l’échantillon seront inférieures à 36 % ou supérieures à 64 % dans 21 % des cas seulement ; vous obtiendrez un vrai positif dans 21 % des cas seulement, et un faux négatif dans 79 % des cas. De toute évidence, un échantillon de 50 est trop petit pour cette expérience ; il ne donnerait un résultat significatif que dans 21% des cas, même s’il y a un ratio de 40:60 de poignets droits cassés par rapport aux poignets gauches.
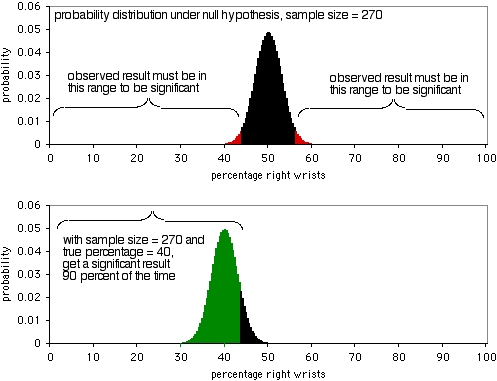

Le graphique suivant montre la distribution de probabilité sous l’hypothèse nulle, avec une taille d’échantillon de 270 individus. Pour être significatif au niveau P<0,05, le résultat observé devrait être inférieur à 43,7% ou supérieur à 56,3% de personnes se cassant le poignet droit. Comme le montre le deuxième graphique, si le véritable pourcentage est de 40 %, les données de l’échantillon seront aussi extrêmes 90 % du temps. Une taille d’échantillon de 270 est assez bonne pour cette expérience ; elle donnerait un résultat significatif dans 90 % des cas s’il y a un rapport de 40:60 entre les poignets droits et les poignets gauches cassés. Si le ratio de poignets droits cassés par rapport aux poignets gauches est plus éloigné de 50:50, vous aurez une probabilité encore plus élevée d’obtenir un résultat significatif.
Exemples
Vous prévoyez de croiser des pois hétérozygotes pour la couleur Jaune/vert du pois, où Jaune est dominant. Le ratio attendu dans la descendance est de 3 jaune : 1 vert. Vous voulez savoir si les pois jaunes sont en fait plus ou moins adaptés, ce qui pourrait se traduire par une proportion de pois jaunes différente de celle attendue. Vous décidez arbitrairement que vous voulez une taille d’échantillon qui détectera une différence significative (P<0,05) s’il y a 3 % de pois jaunes de plus ou de moins que prévu, avec une puissance de 90 %. Vous testerez les données à l’aide du test binomial exact de qualité d’ajustement si la taille de l’échantillon est suffisamment petite, ou d’un test G de qualité d’ajustement si la taille de l’échantillon est plus grande. L’analyse de puissance est la même pour les deux tests.
En utilisant G*Power comme décrit pour le test exact de goodness-of-fit, le résultat est qu’il faudrait 2109 plants de pois si vous voulez obtenir un résultat significatif (P<0,05) dans 90 % des cas, si la vraie proportion de pois jaunes est de 78 %, et 2271 pois si la vraie proportion est de 72 % de jaunes. Comme vous êtes intéressé par un écart dans l’une ou l’autre direction, vous utilisez le plus grand nombre, 2271. C’est beaucoup de pois, mais vous êtes rassuré de voir que ce n’est pas un nombre ridicule. Si vous voulez détecter une différence de 0,1% entre le nombre attendu et le nombre observé de pois jaunes, vous pouvez calculer que vous aurez besoin de 1 970 142 pois ; si c’est ce que vous devez détecter, l’analyse de la taille de l’échantillon vous indique que vous allez devoir inclure un robot trieur de pois dans votre budget.
Les données d’exemple pour le test t à deux échantillons montrent que la taille moyenne dans la section de 14 h de l’analyse des données biologiques était de 66,6 pouces et que la taille moyenne dans la section de 17 h était de 64,6 pouces, mais la différence n’est pas significative (P=0,207). Vous souhaitez savoir combien d’élèves vous devriez échantillonner pour avoir 80 % de chances qu’une différence aussi importante soit significative. À l’aide de G*Power, comme décrit sur la page du test t à deux échantillons, entrez 2,0 pour la différence entre les moyennes. À l’aide de la fonction STDEV d’Excel, calculez l’écart type pour chaque échantillon dans les données originales ; il est de 4,8 pour l’échantillon 1 et de 3,6 pour l’échantillon 2. Entrez 0,05 pour alpha et 0,80 pour la puissance. Le résultat est 72, ce qui signifie que si les élèves de 17 heures étaient vraiment plus courts de deux pouces que ceux de 14 heures, il faudrait 72 élèves dans chaque classe pour détecter une différence significative 80 % du temps, si la vraie différence est vraiment de 2,0 pouces.
Comment faire des analyses de puissance
G*Power
G*Power est un excellent programme gratuit, disponible pour Mac et Windows, qui fera des analyses de puissance pour une grande variété de tests. J’expliquerai comment utiliser G*Power pour des analyses de puissance pour la plupart des tests de ce manuel.
R
Salvatore Mangiafico’s R Companion a des exemples de programmes R pour faire des analyses de puissance pour de nombreux tests de ce manuel ; allez à la page pour le test individuel et faites défiler jusqu’en bas pour le programme d’analyse de puissance.
SAS
SAS a un PROC POWER que vous pouvez utiliser pour les analyses de puissance. Vous entrez les paramètres nécessaires (qui varient en fonction du test) et saisissez une période (qui symbolise les données manquantes dans SAS) pour le paramètre que vous résolvez (généralement ntotal, la taille totale de l’échantillon, ou npergroup, le nombre d’échantillons dans chaque groupe). Je trouve que G*Power est plus facile à utiliser que SAS à cette fin, donc je ne recommande pas d’utiliser SAS pour vos analyses de puissance.
⇐ Previous topic|Next topic ⇒ Table of Contents
Cette page a été révisée pour la dernière fois le 20 juillet 2015. Son adresse est http://www.biostathandbook.com/power.html. Elle peut être citée comme suit :
McDonald, J.H. 2014. Manuel de statistiques biologiques (3e édition). Sparky House Publishing, Baltimore, Maryland. Cette page web contient le contenu des pages 40 à 44 de la version imprimée.
©2014 par John H. McDonald. Vous pouvez probablement faire ce que vous voulez de ce contenu ; voir la page des autorisations pour plus de détails.
.