

En l’an 1072 de notre ère, Omar Khayyam a documenté la longueur d’année la plus précise jamais calculée – un chiffre encore suffisamment précis pour la plupart des usages dans le monde moderne. Khayyam était un astronome, un astrologue, un médecin, un philosophe et un mathématicien : il a apporté des contributions exceptionnelles à l’algèbre. Sa poésie est plus connue en Occident que celle de tout autre poète non occidental.
L’homme lui-même reste une sorte d’énigme. Différents biographes l’ont décrit comme un agnostique aimant s’amuser et buvant du vin, un zoroastrien refoulé, un musulman soufi, un musulman sunnite orthodoxe et un adepte de la philosophie grecque antique. Tous s’accordent à dire qu’il était un intellectuel hors du commun.
Débuts
Omar Khayyam est né le 18 mai 1048 dans la grande ville commerçante de Nishapur, au nord de la Perse. Cette ville se trouve aujourd’hui en Iran. Le père d’Omar était Ebrahim Khayyami, un riche médecin. Le nom de la mère d’Omar n’est pas connu. Certains auteurs ont écrit que le père d’Omar gagnait sa vie en fabriquant des tentes, car Khayyami signifie fabricant de tentes. Cependant, bien que de nombreux anglophones s’appellent Smith, cela ne signifie pas que leurs pères passaient leurs journées à marteler du métal chaud sur une enclume.
La famille d’Omar était musulmane. Son père semble avoir été détendu en matière de religion, employant un mathématicien du nom de Bahmanyar bin Marzban, un adepte de l’ancienne religion perse du zoroastrisme, pour donner des cours particuliers à Omar. Bahmanyar avait été l’élève du grand médecin, scientifique et philosophe Avicenne, et il a donné à Omar une éducation approfondie en science, philosophie et mathématiques. Khawjah al-Anbari a enseigné l’astronomie à Omar, le guidant à travers l’Almageste de Ptolémée.
Au début de son adolescence, Omar a travaillé dans le cabinet de son père pour apprendre la médecine.
Omar Khayyam a fêté son dix-huitième anniversaire en 1066. La même année, la comète de Halley est apparue dans le ciel, l’armée normande de Guillaume le Conquérant a envahi l’Angleterre et le père d’Omar, Ebrahim, est mort. Quelques mois après la mort d’Ebrahim, Bahmanyar, le tuteur d’Omar, est également décédé.
C’était la fin d’une époque dans la vie d’Omar Khayyam. Il était temps de mettre de l’ordre dans les affaires de sa famille et de passer à autre chose.
Samarkand
Omar Khayyam a rejoint l’une des caravanes régulières faisant un voyage de trois mois de Nishapur à la grande ville de Samarkand, qui se trouve maintenant en Ouzbékistan. Samarcande était un centre d’érudition, et Khayyam y est arrivé probablement en 1068, à l’âge de 20 ans.
À Samarcande, il est entré en contact avec le vieil ami de son père, Abu Tahir, qui était gouverneur et juge en chef de la ville. Tahir, observant l’extraordinaire talent de Khayyam pour les chiffres, lui offre un emploi dans son bureau. Bientôt, Khayyam se voit confier un emploi dans le trésor du roi.
Pendant son séjour à Samarcande, Khayyam fait une avancée majeure en algèbre.
Les contributions d’Omar Khayyam à la science
Algèbre
Au lycée, on apprend les équations de la forme ax2 + bx + c = 0 ; on les appelle des équations quadratiques. Les équations cubiques sont de la forme ax3 + bx2 + cx + d = 0. Naturellement, les équations cubiques sont plus difficiles à résoudre que les quadratiques.
Khayyam a conjecturé à juste titre qu’il n’est pas possible de résoudre les équations cubiques en utilisant les outils géométriques traditionnels de la Grèce antique que sont la règle et le compas. D’autres méthodes sont nécessaires.
À l’âge de 22 ans, en 1070, Khayyam publie l’une de ses plus grandes œuvres : Traité de démonstration des problèmes d’algèbre et d’équilibrage. Il y démontre qu’une équation cubique peut avoir plus d’une solution. Il a également montré comment les intersections de sections coniques telles que les paraboles et les cercles peuvent être utilisées pour obtenir des solutions géométriques d’équations cubiques. Archimède avait en fait commencé à travailler dans ce domaine plus de mille ans auparavant, lorsqu’il s’est penché sur le problème spécifique de la détermination du rapport entre le volume d’une partie d’une sphère et celui d’une autre. Khayyam a considéré le problème d’une manière plus générale et méthodique.
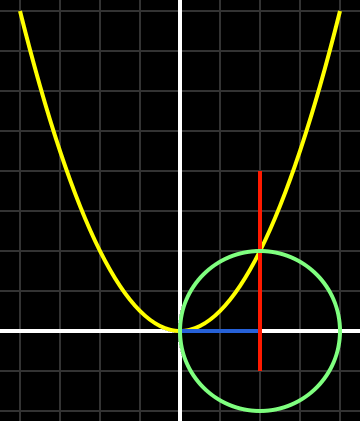
Dans le langage des mathématiques modernes, la solution de Khayyam à l’équation x3 + a2x = b comporte une parabole d’équation x2 = ay, un cercle de diamètre b/a2, et une ligne verticale passant par le point d’intersection. La solution est donnée par la distance sur l’axe des x entre l’origine et la ligne verticale (rouge). Image de Pieter Kuiper.
Les solutions de Khayyam évitaient les coefficients négatifs et les racines négatives car les nombres négatifs n’étaient pas reconnus dans les mathématiques islamiques. (Certaines cultures, cependant, avaient intégré les nombres négatifs dans les mathématiques – par exemple Brahmagupta avait introduit les nombres négatifs dans les mathématiques indiennes 400 ans plus tôt.)
Bien que la réalisation de Khayyam soit magnifique, il était personnellement déçu d’avoir dû utiliser la géométrie pour résoudre les équations cubiques – il avait espéré découvrir un algorithme utilisant uniquement l’algèbre.
Traité de démonstration des problèmes d’algèbre et d’équilibre a établi Khayyam comme un mathématicien de premier rang, et sa réputation s’est rapidement répandue dans toute la Perse.
Après la percée de Khayyam, il y eut peu de progrès significatifs sur les équations cubiques jusqu’en 1535, lorsque Niccolo Tartaglia trouva des solutions générales pour toutes les équations cubiques.
L’algèbre de Khayyam n’était pas le système de lettres et de signes que nous utilisons aujourd’hui. Son algèbre était exprimée en mots. Ainsi, là où aujourd’hui nous écrivons :
Solvez pour x :
x2 + 6 = 5x
Khayyam a écrit : Quelle est la quantité d’un carré pour que lorsqu’on lui ajoute 6 dirhams, il devienne égal à cinq racines de ce carré ?
Lier l’algèbre et la géométrie
L’algèbre et la géométrie ont été liées avec succès par Pierre de Fermat et René Descartes dans les années 1600, ce qui a donné le système moderne de coordonnées x-y.
Le travail de Khayyam sur les cubiques l’avait rendu certain que l’algèbre et la géométrie étaient liées, et il citait les Éléments d’Euclide pour appuyer cette idée :
Quiconque pense que l’algèbre est une astuce pour obtenir des inconnues l’a pensé en vain. Il ne faut pas prêter attention au fait que l’algèbre et la géométrie sont différentes en apparence. Les algèbres sont des faits géométriques qui sont prouvés par les propositions 5 et 6 du livre 2 des Éléments d’Euclide.
Longueur de l’année
En 1073, Khayyam reçoit une invitation dans la ville perse d’Ispahan, capitale de l’empire seldjoukide, pour préparer un calendrier qui fonctionnerait de manière ordonnée et serait précis à jamais – c’était une époque où la longueur des années était régulièrement modifiée.
L’invitation de Khayyam émanait des deux hommes les plus puissants de l’empire seldjoukide, dont la Perse faisait partie : il s’agissait de Malik Shah, sultan de l’empire, et de Nizam al-Mulk, son vizir.
Khayyam a recruté d’autres scientifiques talentueux pour l’accompagner à Ispahan en 1074. Là, il recevait un salaire extraordinairement élevé et bénéficiait d’un mode de vie privilégié. Malik Shah paya Khayyam pour fonder un observatoire dont l’objectif initial était de faire des observations du ciel pendant 30 ans, période pendant laquelle Saturne, la planète la plus lointaine alors connue, accomplirait une orbite.
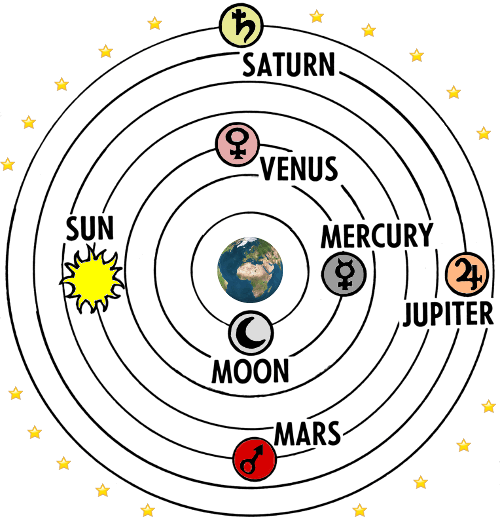
L’univers de Ptolémée – le modèle accepté par Omar Khayyam.
Pendant son séjour à Ispahan, Khayyam a mesuré la durée d’une année – pour être précis la durée de l’année tropicale – avec une exactitude et une précision remarquables.
Khayyam a trouvé que 1 029 983 jours faisaient 2 820 années. Cela donne une longueur d’année tropicale de 365,2422 jours à sept chiffres significatifs. Bien qu’il soit devenu à la mode de citer plus de décimales que cela, l’entrée de Khayyam de 1 029 983 jours contient sept chiffres significatifs, il n’est donc pas raisonnable de citer plus que ce nombre de chiffres significatifs dans la longueur de l’année calculée.
Nous savons aujourd’hui que la longueur d’une année tropicale change en réalité de 30 minutes d’une année à l’autre. La durée moyenne d’une année tropicale citée aujourd’hui est de 365,242189 jours, ce qui, à sept chiffres significatifs près, donne 365,2422 jours – exactement le chiffre auquel Khayyam est arrivé il y a presque mille ans. La durée d’une année tropicale augmente également très légèrement au fil du temps, mais pas suffisamment entre l’époque de Khayyam et la nôtre pour être perceptible sur une échelle de sept chiffres significatifs.
Malik Shah a introduit le nouveau calendrier de Khayyam dans l’empire seldjoukide le 15 mars 1079. Il fut utilisé jusqu’au 20ème siècle.
Le postulat du parallèle
Les 13 livres des Éléments d’Euclide publiés vers 300 avant JC furent probablement les livres les plus influents de toute l’histoire des mathématiques. Les Éléments avaient été construits sur cinq postulats géométriques – en d’autres termes, cinq choses supposées vraies en géométrie : par exemple, tous les angles droits sont égaux entre eux.
Le cinquième des cinq postulats d’Euclide était le postulat du parallèle. Le postulat parallèle s’est avéré être une source de perplexité, d’irritation et de joie pour les mathématiciens pendant des millénaires. La joie était généralement de courte durée, appartenant aux mathématiciens qui pensaient avoir prouvé le postulat pour être déçus lorsqu’une erreur était identifiée dans leur » preuve « .
Euclide avait considéré une ligne droite croisant deux autres lignes droites. Il a examiné la situation dans laquelle les angles intérieurs (montrés dans l’image ci-dessous) font une somme inférieure à 180 degrés. Dans ces circonstances, il a dit que les deux lignes droites se rencontreront éventuellement du côté des deux angles dont la somme est inférieure à 180 degrés.
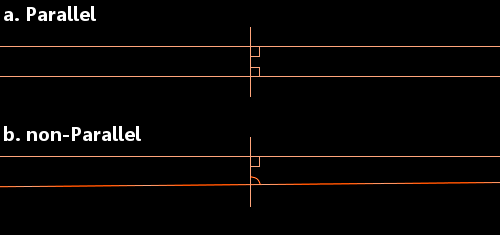
a. Lorsque chaque angle est de 90 degrés, les lignes sont parallèles.
b. Si l’un ou les deux angles sont inférieurs à 90 degrés, les lignes se rencontrent.
Depuis la première publication des Éléments, les mathématiciens avaient essayé d’utiliser les quatre premiers postulats d’Euclide pour prouver le postulat du parallèle. Ils étaient voués à l’échec. Nous savons maintenant qu’il est impossible de prouver le postulat du parallèle en utilisant les autres postulats d’Euclide.
La tentative d’Omar Khayyam était intéressante. Dans ses Explications des difficultés des postulats des Éléments d’Euclide, il demande à ses lecteurs de considérer une ligne droite AB :


Il demande à ses lecteurs de considérer deux lignes égales perpendiculaires à AB et voit trois arrangements possibles, qui peuvent produire des figures à quatre côtés :


Il réfute ensuite la possibilité que les angles C et/ou D puissent être autre chose que des angles droits et dans l’image ci-dessus, seule l’option centrale est possible. Ainsi, il croit avoir prouvé le postulat du parallèle. En fait, il ne l’a pas fait, il n’a fait que l’énoncer d’une manière différente.
Ce qui est intéressant pour les historiens des mathématiques, c’est que dans les idées de Khayyam – montrées grossièrement dans les images ci-dessus – ils peuvent voir les premières lueurs de la géométrie non-euclidienne.
Quelques détails personnels et la fin
Les détails complets de la vie personnelle de Khayyam ne sont pas connus. On pense qu’il s’est marié et a eu au moins un fils et une fille.
En 1092, Malik Shah et son vizir sont tous deux morts – le premier probablement par empoisonnement, le second par assassinat. Khayyam s’est caché pendant la lutte pour le pouvoir qui en a résulté. Sa survie dépendait de sa discrétion. Il avait été le médecin personnel de Malik Shah et était devenu son ami personnel proche – ce qui lui avait valu des ennemis – et la poésie de Khayyam suggère que son comportement n’était peut-être pas très religieux – ce qui lui avait également valu des ennemis. Khayyam n’a en fait publié aucun poème de son vivant. Certaines de ses rêveries auraient potentiellement mis sa vie en danger.
Après la lutte pour le pouvoir, il a fallu environ 20 ans pour que Khayyam soit pleinement réhabilité et qu’il émerge à nouveau, à 64 ans, en compagnie de personnes puissantes. Cependant, il refusait d’enseigner. L’un de ses poèmes suggère la raison de ce refus :
ne peuvent être racontés de peur de perdre la tête;
Puisque personne n’est apte à apprendre, ou ne se soucie de savoir,
Il vaut mieux que toutes mes pensées restent non dites.
Omar Khayyam est mort à l’âge de 83 ans dans sa ville natale de Nishapur le 4 décembre 1131. Il fut enterré dans une tombe dont il avait choisi l’emplacement dans un verger où les fleurs tombaient deux fois par an.
La poésie de Khayyam a été popularisée dans les années 1800 par les traductions d’Edward FitzGerald dans les Rubaiyat d’Omar Khayyam. Khayyam est devenu si admiré en Occident qu’en 1963, le Shah d’Iran a fait exhumer sa tombe et déplacer les restes de Khayyam dans un immense mausolée construit à cet effet à Nishapur, où les touristes peuvent rendre hommage au grand poète.
Nous terminerons par l’un des quatrains les plus célèbres et les plus évocateurs de Khayyam :
Une cruche de vin, un pain et toi
À côté de moi chantant dans la nature sauvage-
Et la nature sauvage est un paradis en soi. »
Auteur de cette page : Le Doc
Images améliorées numériquement et colorisées par ce site. © Tous droits réservés.
Citer cette page
Veuillez utiliser la citation suivante conforme à la norme MLA :
"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.
Publiée par FamousScientists.org
Lecture complémentaire
Edward FitzGerald (traducteur)
The Rubaiyat of Omar Khayyam
Howard Willford Bell, 1901
Victor J. Katz
A History of Mathematics : An Introduction
HarperCollins College Publishers, New York, 1993
Roshdi Rashed (Editor)
Encyclopédie de l’histoire des sciences arabes
Routledge, 1996
Histoire de l’astronomie – Moyen-Orient
ephemeris.com, 2003
Hazhir Teimourian
Omar Khayyam : Poète, rebelle, astronome
The History Press, 2008
Mehdi Aminrazavi
Le vin de la sagesse : La vie, la poésie et la philosophie d’Omar Khayyam
Oneworld Publications, 2013
.