Objectifs d’apprentissage
À la fin de cette section, vous serez en mesure de :
- Définir les forces non conservatives et expliquer comment elles affectent l’énergie mécanique.
- Montrer comment le principe de conservation de l’énergie peut être appliqué en traitant les forces conservatrices en termes d’énergies potentielles et toute force non conservatrice en termes de travail qu’elle effectue.
Forces non conservatrices et frottement
Les forces sont soit conservatrices, soit non conservatrices. Les forces conservatrices ont été abordées dans Forces conservatrices et énergie potentielle. Une force non conservatrice est une force pour laquelle le travail dépend du chemin emprunté. La friction est un bon exemple de force non conservatrice. Comme l’illustre la figure 1, le travail effectué contre la friction dépend de la longueur de la trajectoire entre les points de départ et d’arrivée. En raison de cette dépendance de la trajectoire, il n’y a pas d’énergie potentielle associée aux forces non conservatives. Une caractéristique importante est que le travail effectué par une force non conservatrice ajoute ou retire de l’énergie mécanique à un système. Le frottement, par exemple, crée de l’énergie thermique qui se dissipe, retirant ainsi de l’énergie au système. En outre, même si l’énergie thermique est conservée ou capturée, elle ne peut pas être entièrement reconvertie en travail, elle est donc perdue ou non récupérable dans ce sens également.

Figure 1. La quantité du visage heureux effacé dépend du chemin emprunté par la gomme entre les points A et B, tout comme le travail effectué contre la friction. Le travail effectué et la quantité de visage effacé sont moindres pour le chemin en (a) que pour le chemin en (b). La force est ici la friction, et la majeure partie du travail se transforme en énergie thermique qui quitte ensuite le système (le visage heureux plus la gomme). L’énergie dépensée ne peut pas être entièrement récupérée.
Comment les forces non conservatrices affectent l’énergie mécanique
L’énergie mécanique peut ne pas être conservée lorsque des forces non conservatrices agissent. Par exemple, lorsqu’une voiture est amenée à s’arrêter par friction sur un sol plat, elle perd de l’énergie cinétique, qui est dissipée sous forme d’énergie thermique, ce qui réduit son énergie mécanique. La figure 2 compare les effets des forces conservatrices et non conservatrices. Nous choisissons souvent de comprendre d’abord des systèmes plus simples comme celui décrit dans la figure 2a avant d’étudier des systèmes plus compliqués comme dans la figure 2b.

Figure 2. Comparaison des effets des forces conservatrices et non conservatrices sur l’énergie mécanique d’un système. (a) Un système avec uniquement des forces conservatrices. Lorsqu’on laisse tomber une pierre sur un ressort, son énergie mécanique reste constante (en négligeant la résistance de l’air) car la force du ressort est conservatrice. Le ressort peut propulser la pierre à sa hauteur initiale, où elle ne dispose à nouveau que de l’énergie potentielle due à la gravité. (b) Un système avec des forces non conservatrices. Lorsque la même roche est lâchée sur le sol, elle est arrêtée par des forces non conservatives qui dissipent son énergie mécanique sous forme d’énergie thermique, de son et de déformation de la surface. La roche a perdu de l’énergie mécanique.
Comment s’applique le théorème travail-énergie
Envisageons maintenant quelle forme prend le théorème travail-énergie lorsque des forces conservatrices et non conservatrices agissent. Nous verrons que le travail effectué par les forces non conservatrices est égal à la variation de l’énergie mécanique d’un système. Comme indiqué dans l’article L’énergie cinétique et le théorème travail-énergie, le théorème travail-énergie stipule que le travail net sur un système est égal à la variation de son énergie cinétique, ou Wnet = ΔKE. Le travail net est la somme du travail des forces non conservatrices plus le travail des forces conservatrices. C’est-à-dire,
Wnet = Wnc + Wc,
de sorte que
Wnc + Wc = ΔKE,
où Wnc est le travail total effectué par toutes les forces non conservatrices et Wc est le travail total effectué par toutes les forces conservatrices.

Figure 3. Une personne pousse une caisse sur une rampe, effectuant un travail sur la caisse. La friction et la force gravitationnelle (non représentée) effectuent également un travail sur la caisse ; ces deux forces s’opposent à la poussée de la personne. Au fur et à mesure que la caisse est poussée vers le haut de la rampe, elle gagne de l’énergie mécanique, ce qui implique que le travail effectué par la personne est supérieur au travail effectué par la friction.
Considérez la figure 3, dans laquelle une personne pousse une caisse vers le haut d’une rampe et est opposée par la friction. Comme dans la section précédente, nous notons que le travail effectué par une force conservatrice provient d’une perte d’énergie potentielle gravitationnelle, de sorte que Wc = -ΔPE. En substituant cette équation à la précédente et en résolvant Wnc, on obtient
Wnc = ΔKE + ΔPE.
Cette équation signifie que l’énergie mécanique totale (KE + PE) change exactement de la quantité de travail effectué par les forces non conservatrices. Dans la figure 3, il s’agit du travail effectué par la personne moins le travail effectué par la friction. Ainsi, même si l’énergie n’est pas conservée pour le système d’intérêt (comme la caisse), nous savons qu’une quantité égale de travail a été effectuée pour provoquer le changement de l’énergie mécanique totale.
Nous réarrangeons Wnc = ΔKE + ΔPE pour obtenir
KEi + PEi + Wnc = KEf + PEf.
Cela signifie que la quantité de travail effectuée par les forces non conservatives s’ajoute à l’énergie mécanique d’un système. Si Wnc est positif, alors l’énergie mécanique augmente, comme lorsque la personne pousse la caisse sur la rampe de la figure 3. Si Wnc est négatif, l’énergie mécanique diminue, comme lorsque le rocher frappe le sol dans la figure 2b. Si Wnc est égal à zéro, l’énergie mécanique est conservée et les forces non conservatrices sont équilibrées. Par exemple, lorsque vous poussez une tondeuse à gazon à vitesse constante sur un sol plat, votre travail effectué est supprimé par le travail de friction, et la tondeuse a une énergie constante.
Application de la conservation de l’énergie avec des forces non conservatrices
Lorsqu’il n’y a pas de changement d’énergie potentielle, appliquer KEi + PEi + Wnc = KEf + PEf revient à appliquer le théorème du travail et de l’énergie en fixant le changement d’énergie cinétique comme étant égal au travail net effectué sur le système, ce qui, dans le cas le plus général, inclut les forces conservatrices et non conservatrices. Mais lorsqu’on cherche plutôt à trouver un changement d’énergie mécanique totale dans des situations qui impliquent des changements d’énergie potentielle et cinétique, l’équation précédente KE i + PEi + Wnc = KEf + PEf dit qu’on peut commencer par trouver le changement d’énergie mécanique qui aurait résulté des seules forces conservatrices, y compris les changements d’énergie potentielle, et y ajouter le travail effectué, avec le signe approprié, par toute force non conservatrice impliquée.
Exemple 1. Calcul de la distance parcourue : Quelle distance un joueur de baseball glisse-t-il
Envisagez la situation illustrée à la figure 4, où un joueur de baseball glisse jusqu’à l’arrêt sur un terrain plat. En utilisant des considérations énergétiques, calculez la distance sur laquelle le joueur de baseball de 65,0 kg glisse, étant donné que sa vitesse initiale est de 6,00 m/s et que la force de frottement contre lui est une constante de 450 N.

Figure 4. Le joueur de baseball glisse jusqu’à l’arrêt sur une distance d. Au cours de ce processus, le frottement élimine l’énergie cinétique du joueur en effectuant une quantité de travail égale à l’énergie cinétique initiale.
Stratégie
Le frottement arrête le joueur en convertissant son énergie cinétique en d’autres formes, notamment en énergie thermique. En termes de théorème travail-énergie, le travail effectué par la friction, qui est négatif, est ajouté à l’énergie cinétique initiale pour la réduire à zéro. Le travail effectué par la friction est négatif, car f est dans la direction opposée du mouvement (c’est-à-dire θ = 180º, et donc cos θ = -1). Ainsi, Wnc = -fd. L’équation se simplifie en
\frac{1}{2}{mv_{\text{i}}^2-fd=0\\\
ou
fd=\frac{1}{2}{mv_{\text{i}}^2\\\\.
Cette équation peut maintenant être résolue pour la distance d.
Solution
En résolvant l’équation précédente pour d et en substituant les valeurs connues, on obtient
\begin{array}{lll}d&&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0\text{ kg})(6,00\text{ m/s})^2}{(2)(450\text{ N})}\\text{ }&&2.60\text{ m}\end{array}\\
Discussion
Le point le plus important de cet exemple est que la quantité de travail non-conservateur est égale au changement d’énergie mécanique. Par exemple, vous devez travailler plus fort pour arrêter un camion, avec sa grande énergie mécanique, que pour arrêter un moustique.
Exemple 2. Calcul de la distance parcourue : Glisser sur une pente
Supposons que le joueur de l’exemple 1 court sur une colline ayant une inclinaison de 5,00º vers le haut avec une surface similaire à celle du stade de baseball. Le joueur glisse avec la même vitesse initiale. Déterminez quelle distance il glisse.

Figure 5. Le même joueur de baseball glisse jusqu’à l’arrêt sur une pente de 5,00º.
Stratégie
Dans ce cas, le travail effectué par la force de friction non conservatrice sur le joueur réduit l’énergie mécanique qu’il possède de son énergie cinétique à hauteur zéro, à l’énergie mécanique finale qu’il possède en se déplaçant sur une distance d pour atteindre la hauteur h le long de la colline, avec h = d sin 5,00º. Ceci est exprimé par l’équation KE + PEi + Wnc = KE f + PEf.
Solution
Le travail fourni par la friction est à nouveau Wnc = -fd ; initialement, l’énergie potentielle est PEi = mg – 0 = 0 et l’énergie cinétique est \text{KE}_{\text{i}}=\frac{1}{2}mv_{\text{i}}^2\\\\ ; les contributions énergétiques finales sont KEf = 0 pour l’énergie cinétique et PEf = mgh = mgd sin θ pour l’énergie potentielle.
La substitution de ces valeurs donne
\frac{1}{2}{mv_{\text{i}}^2+0+\left(-fd\right)=0+mgd\sin\theta\\\
Solvez ceci pour d afin d’obtenir
\begin{array}{lll}d&&\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65,0\text{ kg})(6,00\text{ m/s})^2}{450\text{ N}+(65,0\text{ kg})\gauche(9,80\text{ m/s}^2\droite)\sin(5,00^{\circ})}\&&2.31\text{ m}\end{array}\\
Discussion
Comme on pouvait s’y attendre, le joueur glisse sur une distance plus courte en glissant en montée. Notez que le problème aurait également pu être résolu en termes de forces directement et du théorème de l’énergie de travail, au lieu d’utiliser l’énergie potentielle. Cette méthode aurait nécessité de combiner les vecteurs de la force normale et de la force de gravité, qui ne s’annulent plus car ils pointent dans des directions différentes, et la friction, pour trouver la force nette. Vous pourriez ensuite utiliser la force nette et le travail net pour trouver la distance d qui réduit l’énergie cinétique à zéro. En appliquant la conservation de l’énergie et en utilisant l’énergie potentielle à la place, nous devons seulement considérer l’énergie potentielle gravitationnelle mgh, sans combiner et résoudre les vecteurs de force. Cela simplifie considérablement la solution.
Making Connections : Investigation à emporter – Déterminer la friction à partir de la distance d’arrêt
Cette expérience implique la conversion de l’énergie potentielle gravitationnelle en énergie thermique. Utilisez la règle, le livre et la bille de la section « Making Connections » de l’énergie potentielle gravitationnelle. En outre, vous aurez besoin d’un gobelet en mousse avec un petit trou sur le côté, comme illustré à la figure 6. À partir de la position de 10 cm sur la règle, faites rouler la bille dans le gobelet placé au bas de la règle. Mesurez la distance d que le gobelet parcourt avant de s’arrêter. Quelles forces ont provoqué cet arrêt ? Qu’est-il arrivé à l’énergie cinétique de la bille au bas de la règle ? Ensuite, placez la bille aux positions 20 cm et 30 cm et mesurez à nouveau la distance parcourue par le gobelet après l’entrée de la bille. Tracez la distance de déplacement de la tasse en fonction de la position initiale de la bille sur la règle. Cette relation est-elle linéaire ?
Avec quelques hypothèses simples, vous pouvez utiliser ces données pour trouver le coefficient de friction cinétique μk de la tasse sur la table. La force de friction f sur la tasse est de μkN, où la force normale N est juste le poids de la tasse plus la bille. La force normale et la force de gravité n’effectuent aucun travail car elles sont perpendiculaires au déplacement de la tasse, qui se déplace horizontalement. Le travail effectué par la friction est fd. Vous aurez également besoin de la masse de la bille pour calculer son énergie cinétique initiale.
Il est intéressant de faire l’expérience ci-dessus également avec une bille en acier (ou un roulement à billes). En la relâchant des mêmes positions sur la règle que vous l’avez fait avec la bille de verre, la vitesse de cette bille d’acier est-elle la même que la vitesse de la bille au bas de la règle ? La distance parcourue par la tasse est-elle proportionnelle à la masse des billes d’acier et de verre ?

Figure 6. Faire rouler une bille le long d’une règle dans un gobelet en mousse.
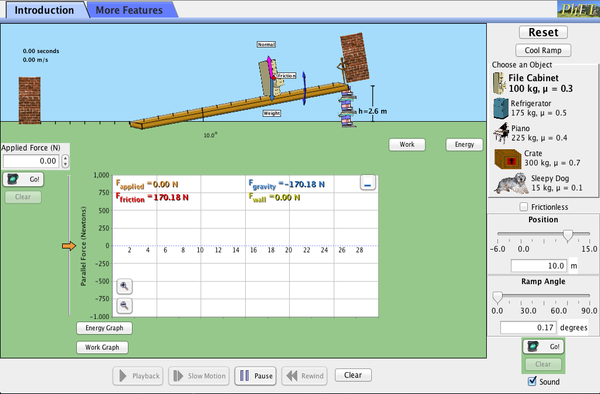
PhET Explorations : La rampe
Explorez les forces, l’énergie et le travail en poussant des objets domestiques vers le haut et le bas d’une rampe. Abaissez et élevez la rampe pour voir comment l’angle d’inclinaison affecte les forces parallèles agissant sur l’armoire à dossiers. Des graphiques montrent les forces, l’énergie et le travail.
Cliquez pour télécharger. Exécuter en utilisant Java.
Résumé de section
- Une force non conservative est une force pour laquelle le travail dépend de la trajectoire.
- La friction est un exemple de force non conservative qui change l’énergie mécanique en énergie thermique.
- Le travail Wnc effectué par une force non conservative change l’énergie mécanique d’un système. Sous forme d’équation, Wnc = ΔKE + ΔPE ou, de manière équivalente, KEi + PEi + Wnc = KEf + PEf.
- Lorsque des forces conservatrices et non conservatrices agissent, la conservation de l’énergie peut être appliquée et utilisée pour calculer le mouvement en fonction des énergies potentielles connues des forces conservatrices et du travail effectué par les forces non conservatrices, au lieu de trouver le travail net à partir de la force nette, ou de devoir appliquer directement les lois de Newton.
Problèmes & Exercices
- Un skieur de 60,0 kg ayant une vitesse initiale de 12,0 m/s gravit en roue libre une montée de 2,50 m de haut, comme le montre la figure 7. Trouvez sa vitesse finale au sommet, sachant que le coefficient de friction entre ses skis et la neige est de 0,0800. (Indice : trouvez la distance parcourue sur la pente en supposant une trajectoire en ligne droite comme indiqué sur la figure.)

Figure 7. L’énergie cinétique initiale du skieur est partiellement utilisée pour atteindre le sommet d’une montée en roue libre.
- (a) A quelle hauteur une voiture peut-elle monter en roue libre (moteur débrayé) si le travail effectué par le frottement est négligeable et si sa vitesse initiale est de 110 km/h ? (b) Si, dans la réalité, on observe qu’une voiture de 750 kg ayant une vitesse initiale de 110 km/h gravit une colline en roue libre jusqu’à une hauteur de 22,0 m au-dessus de son point de départ, quelle quantité d’énergie thermique a été générée par la friction ? (c) Quelle est la force moyenne de friction si la colline a une pente de 2,5º au-dessus de l’horizontale ?
Glossaire
Force non conservative : une force dont le travail dépend du chemin suivi entre les configurations initiale et finale données
friction : la force entre des surfaces qui s’oppose à ce qu’une glisse sur l’autre ; le frottement transforme l’énergie mécanique en énergie thermique
Solutions choisies de problèmes & Exercices
1. 9,46 m/s
.