Qu’est-ce que l’analyse factorielle ?
L’analyse factorielle est la pratique consistant à condenser de nombreuses variables en quelques-unes seulement, afin que vos données de recherche soient plus faciles à travailler.
La théorie est qu’il existe des facteurs plus profonds conduisant les concepts sous-jacents dans vos données, et que vous pouvez découvrir et travailler avec ceux-ci au lieu de traiter les variables de niveau inférieur qui en découlent. L’analyse factorielle est aussi parfois appelée « réduction des dimensions ». Vous pouvez réduire les « dimensions » de vos données en une ou plusieurs « super-variables », également appelées variables non observées ou variables latentes.
Ces concepts plus profonds ne sont pas immédiatement évidents. Ils pourraient représenter des traits ou des tendances difficiles à mesurer, comme l’extraversion ou le QI.
Comme pour tout type de processus qui simplifie la complexité, il y a un compromis entre la précision des données et la facilité à travailler avec elles. Avec l’analyse factorielle, la meilleure solution est celle qui donne une simplification qui représente la vraie nature de vos données, avec une perte minimale de précision.
L’analyse factorielle n’est pas une technique unique, mais une famille de méthodes statistiques qui peuvent être utilisées pour identifier les facteurs latents qui pilotent les variables observables. L’analyse factorielle est couramment utilisée dans les études de marché, ainsi que dans d’autres disciplines comme la technologie, la médecine, la sociologie, la biologie de terrain, l’éducation, la psychologie et bien d’autres encore.
eBook : 8 innovations pour moderniser les études de marché
Concepts clés de l’analyse factorielle
L’une des idées les plus importantes de l’analyse factorielle est la variance – à quel point vos valeurs numériques diffèrent de la moyenne. Lorsque vous effectuez une analyse factorielle, vous cherchez à comprendre comment les différents facteurs sous-jacents influencent la variance parmi vos variables. Chaque facteur aura une influence, mais certains expliqueront plus de variance que d’autres, ce qui signifie que le facteur représente plus précisément les variables qui le composent.
La quantité de variance qu’un facteur explique est exprimée par une valeur propre. Si une solution factorielle a une valeur propre de 1 ou plus, elle explique plus de variance qu’une seule variable observée – ce qui signifie qu’elle peut vous être utile pour réduire votre nombre de variables. Les solutions factorielles dont la valeur propre est inférieure à 1 expliquent moins de variance qu’une seule variable et ne sont pas retenues dans l’analyse. En ce sens, une solution contiendrait moins de facteurs que le nombre initial de variables.
Une autre métrique importante est le score factoriel. Il s’agit d’une mesure numérique qui décrit à quel point une variable des données de recherche originales est liée à un facteur donné. Un autre terme pour cette association ou pondération vers un certain facteur est la charge factorielle.
Types d’analyse factorielle
Il existe deux formes de base d’analyse factorielle, exploratoire et confirmatoire. Voici comment elles sont utilisées pour ajouter de la valeur à votre processus de recherche.
Analyse factorielle confirmatoire
Dans ce type d’analyse, le chercheur part d’une hypothèse sur ses données qu’il cherche à prouver ou à infirmer. L’analyse factorielle confirmera – ou non – où se trouvent les variables latentes et quelle part de variance elles représentent.
L’analyse en composantes principales est une forme populaire d’analyse factorielle confirmatoire. En utilisant cette méthode, le chercheur effectuera l’analyse pour obtenir de multiples solutions possibles qui répartissent leurs données entre un certain nombre de facteurs. Les éléments qui se chargent sur un seul facteur sont plus fortement liés les uns aux autres et peuvent être regroupés par le chercheur en utilisant ses connaissances conceptuelles.
L’utilisation de l’ACP générera une gamme de solutions avec différents nombres de facteurs, des solutions simplifiées à 1 facteur aux niveaux de complexité plus élevés. Cependant, moins le nombre de facteurs employés est élevé, moins la variance sera prise en compte dans la solution.
Analyse factorielle exploratoire
Comme son nom l’indique, l’analyse factorielle exploratoire est entreprise sans hypothèse à l’esprit. C’est un processus d’investigation qui aide les chercheurs à comprendre s’il existe des associations entre les variables initiales et, si c’est le cas, où elles se situent et comment elles sont regroupées.
Comment effectuer une analyse factorielle
La plupart des principaux logiciels statistiques, tels que SPSS et Stata, comprennent une fonction d’analyse factorielle que vous pouvez utiliser pour analyser vos données. Pour commencer, vous aurez besoin des variables qui vous intéressent et, le cas échéant, des détails de votre hypothèse initiale sur leurs relations et les variables sous-jacentes.
Comment l’analyse factorielle peut vous aider
En plus de vous donner moins de variables à naviguer, l’analyse factorielle peut vous aider à comprendre le regroupement et le clustering dans vos variables d’entrée, puisqu’elles seront regroupées en fonction des variables latentes.
Supposons que vous posiez plusieurs questions toutes conçues pour explorer des aspects différents, mais étroitement liés, de la satisfaction client :
- À quel point êtes-vous satisfait de notre produit ?
- Pourriez-vous recommander notre produit à un ami ou à un membre de votre famille ?
- Quelle est la probabilité que vous achetiez notre produit à l’avenir ?
Mais vous ne voulez qu’une seule variable pour représenter un score de satisfaction client. Une option serait de faire la moyenne des réponses aux trois questions. Une autre option serait de créer une variable dépendante factorielle. Cela peut être fait en exécutant l’ACP et en conservant la première composante principale (également connue sous le nom de facteur). L’avantage de l’ACP par rapport à une moyenne est qu’elle pondère automatiquement chacune des variables dans le calcul.
Disons que vous avez une liste de questions et que vous ne savez pas exactement quelles réponses évolueront ensemble et lesquelles évolueront différemment ; par exemple, les obstacles à l’achat des clients potentiels. Les éléments suivants sont des barrières à l’achat possibles :
- Le prix est prohibitif
- Les coûts globaux de mise en œuvre
- Nous ne parvenons pas à obtenir un consensus dans notre organisation
- Le produit n’est pas cohérent avec notre stratégie commerciale
- Je dois élaborer un retour sur investissement, mais ne peut pas ou n’a pas pu le faire
- Nous sommes bloqués dans un contrat avec un autre produit
- Les avantages du produit ne compensent pas le coût
- Nous n’avons aucune raison de changer
- Notre département informatique ne peut pas supporter votre produit
- Nous n’avons pas suffisamment de ressources techniques
- Votre produit n’a pas une fonctionnalité dont nous avons besoin
- Autre (veuillez préciser)
.
L’analyse factorielle peut découvrir les tendances de la façon dont ces questions vont évoluer ensemble. Voici les chargements pour 3 facteurs pour chacune des variables.
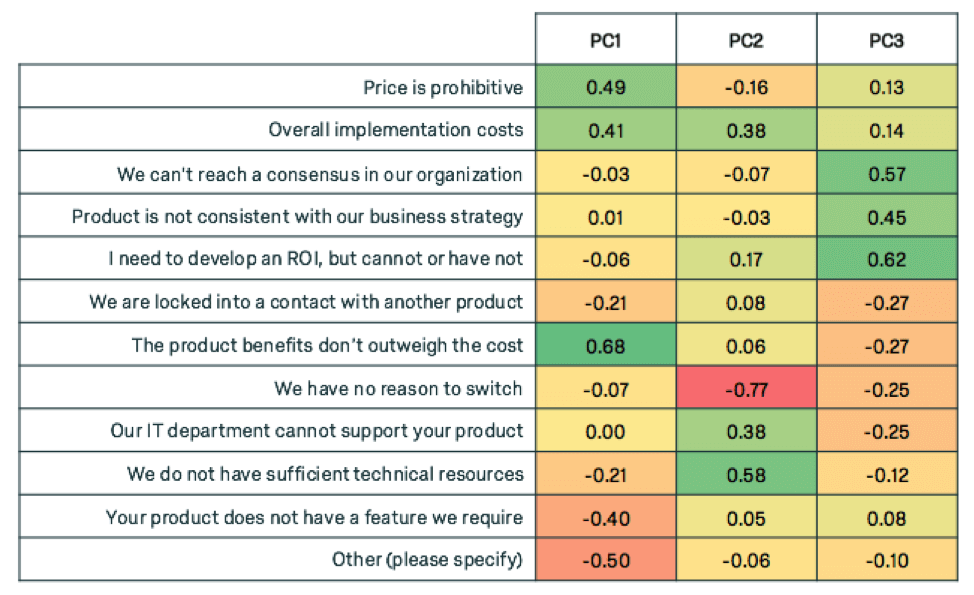
Notez comment chacune des composantes principales a des poids élevés pour un sous-ensemble de variables. La première composante pondère fortement les variables liées au coût, la deuxième pondère les variables liées à l’informatique, et la troisième pondère les variables liées aux facteurs organisationnels. Nous pouvons donner des noms astucieux à nos nouvelles super variables.
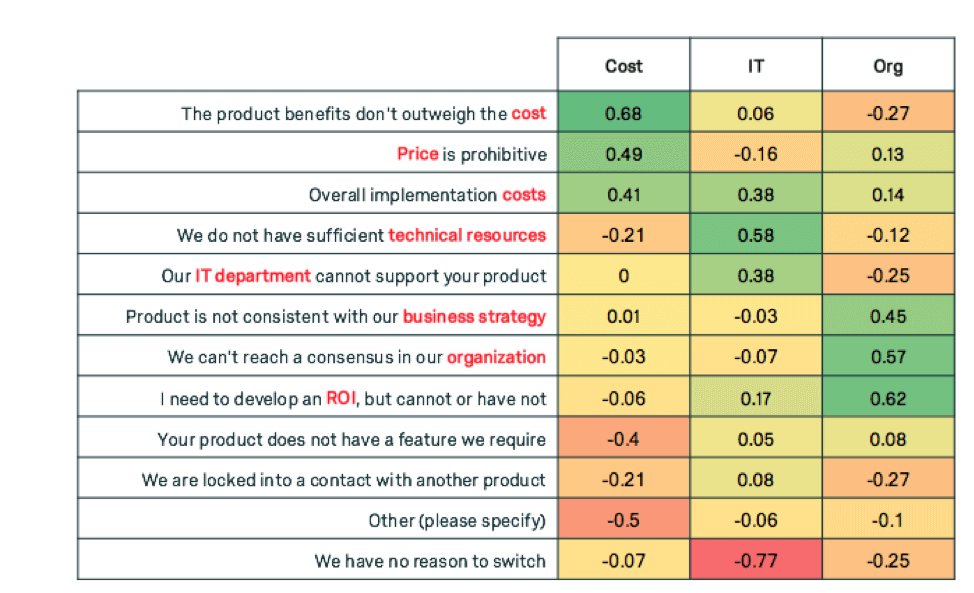 Si nous devions regrouper les clients en fonction de ces trois composantes, nous pourrions observer certaines tendances. Les clients ont tendance à être élevés en ce qui concerne les obstacles liés aux coûts ou les obstacles liés à l’Org, mais pas les deux.
Si nous devions regrouper les clients en fonction de ces trois composantes, nous pourrions observer certaines tendances. Les clients ont tendance à être élevés en ce qui concerne les obstacles liés aux coûts ou les obstacles liés à l’Org, mais pas les deux.
Exemples d’études d’analyse factorielle
L’analyse factorielle, y compris l’ACP, est souvent utilisée en tandem avec des études de segmentation. Il peut s’agir d’une étape intermédiaire pour réduire les variables avant d’utiliser KMeans pour réaliser les segments.
L’analyse factorielle apporte de la simplicité après la réduction des variables. Pour les études longues avec de grands blocs de questions à échelle de Likert Matrix, le nombre de variables peut devenir lourd. La simplification des données à l’aide de l’analyse factorielle aide les analystes à se concentrer et à clarifier les résultats, tout en réduisant le nombre de dimensions sur lesquelles ils effectuent des regroupements.
Questions types
Choisir exactement les questions sur lesquelles effectuer une analyse factorielle est à la fois un art et une science. Choisir les variables à réduire demande un peu d’expérimentation, de patience et de créativité. L’analyse factorielle fonctionne bien sur les questions à échelle de Likert et les types de questions de type Somme à 100.
L’analyse factorielle fonctionne bien sur les blocs matriciels des genres de questions suivants :
Psychographie (d’accord/désaccord) :
- J’accorde de l’importance à la famille
- Je crois que la marque représente une valeur
Comportementaux (D’accord/Désaccord):
- J’achète l’option la moins chère
- Je suis un acheteur à bon marché
Attitudinaux (D’accord/Désaccord) :
- L’économie ne s’améliore pas
- Je suis satisfait du produit
Base sur l’activité (d’accord/désaccord) :
- J’aime le sport
- J’achète parfois en ligne pendant les heures de travail
Les questions comportementales et psychographiques sont particulièrement adaptées à l’analyse factorielle.