Si le nombre de fentes dans un obstacle est important, la netteté du motif est améliorée, les maxima devenant plus étroits. Les obstacles comportant un grand nombre de fentes (plus de 20 par millimètre, par exemple) sont appelés réseaux de diffraction. Ceux-ci ont été développés pour la première fois par Fraunhofer à la fin du XVIIIe siècle et ils consistaient en un fil d’argent fin enroulé sur deux vis parallèles donnant environ 30 obstacles au millimètre.
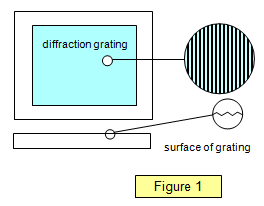
Depuis, de nombreuses améliorations ont été apportées, en 1882, Rowland a utilisé un diamant pour tracer des lignes fines sur du verre, les crêtes jouant le rôle de fentes et les règles celui d’obstacles (voir figure 1). En utilisant cette méthode, il est possible d’obtenir des réseaux de diffraction avec jusqu’à 3000 lignes par millimètre bien que les réseaux » grossiers » avec environ 500 lignes par millimètre soient meilleurs pour un usage général.
Dans de nombreuses écoles, deux types sont couramment utilisés, l’un avec 300 lignes par mm et l’autre avec 80 lignes par mm.
On utilise également des réseaux de réflexion, où l’image diffractée est vue après réflexion sur une surface réglée. Un très bon exemple de réseau de diffraction par réflexion est un CD. Un DVD avec des règles plus fines donne un motif de diffraction beaucoup plus large.
La théorie des ondes et le réseau de diffraction
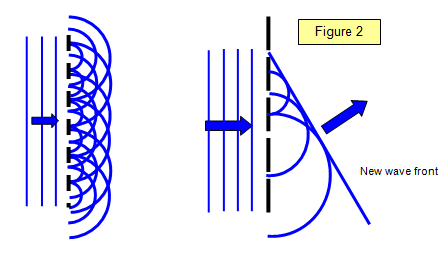
La figure 2 montre la construction de Huygens pour un réseau. Vous pouvez voir comment les ondes diffractées circulaires de chaque fente s’additionnent dans certaines directions pour donner une onde diffractée qui a un front d’onde plan, tout comme les ondes qui frappent le réseau par la gauche. Cette onde plane est formée en traçant la ligne qui rencontre toutes les petites ondes circulaires et est appelée une enveloppe de toutes ces petites ondes secondaires.
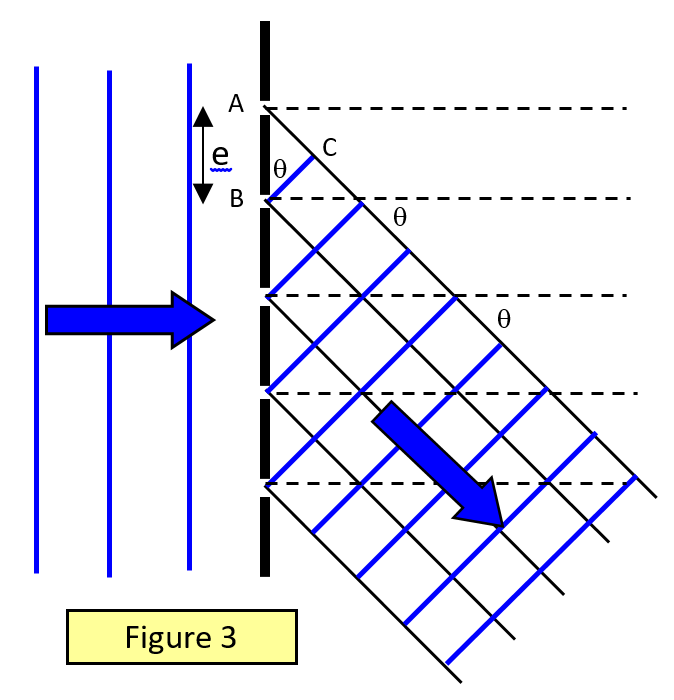
La formule du réseau de diffraction
Considérez un faisceau de lumière parallèle incident normalement sur un réseau de diffraction avec un espacement de réseau e (l’espacement de réseau est l’inverse du nombre de lignes par unité de longueur). Considérez la lumière qui est diffractée à un angle q par rapport à la normale et provenant de points correspondants sur des fentes adjacentes (figure 3).
Pour un maximum, la différence de parcours = AC = mλ
Mais AC = e sinθ. Donc pour un maximum:
mλ = e sinθ
où m = 0, 1, 2,3….
Le nombre m est connu comme l’ordre du spectre, c’est-à-dire qu’un spectre de premier ordre est formé pour m = 1, et ainsi de suite.
Si l’on utilise une lumière d’une seule longueur d’onde, comme celle d’un laser, on obtient une série de lignes nettes, une ligne à chaque ordre du spectre. Avec une source de lumière blanche, une série de spectres se forme, la lumière de la longueur d’onde la plus courte ayant le plus petit angle de diffraction.
En dérivant la formule ci-dessus, nous avons supposé que le faisceau incident est à angle droit avec la face du réseau. Il faut tenir compte du fait que ce n’est pas le cas. La méthode la plus simple consiste à mesurer la position du spectre de premier ordre de part et d’autre du centre, à enregistrer l’angle entre ces positions puis à le diviser par deux, comme le montre la figure 4.
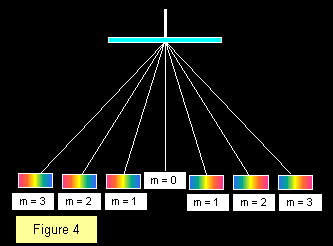
Le nombre d’ordres de spectres visibles avec un réseau donné dépend de l’espacement des réseaux, davantage de spectres étant visibles avec des réseaux plus grossiers. La face réglée du réseau doit toujours être orientée à l’opposé de la lumière incidente pour éviter les erreurs dues aux changements de direction dus à la réfraction dans le verre. Le diagramme montre une frange blanche centrale avec trois spectres de chaque côté donnant un total de sept images.
(Voir exemple de problème )
1. Calculez la longueur d’onde de la lumière monochromatique où l’image de second ordre est diffractée selon un angle de 25o en utilisant un réseau de diffraction de 300 lignes par millimètre.
Espacement du réseau (e) = 10-3/300 m = 3.3×10-6 m
Longueur d’onde (l) = esin25/2 = /2 = 6,97×10-7 m = 697 nm
2. Calculer le nombre maximal d’ordres visibles avec un réseau de diffraction de 500 lignes par millimètre, en utilisant une lumière de longueur d’onde 600 nm.
Angle maximal de diffraction = 90o e = 10-3/500 = 2×10-6 m
Donc m = esinq/l = 2×10-6/600×10-9 = 3,33
Donc le nombre maximal d’ordres = 3, et un total de sept images de la source peut être vu (trois de chaque côté d’une image centrale).
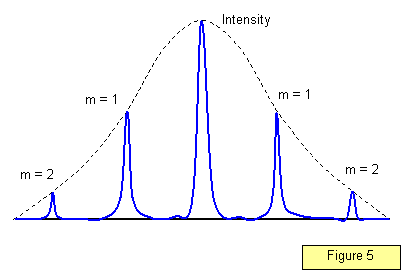
La distribution de l’intensité dans le diagramme de diffraction pour un grand nombre de fentes est représentée sur la figure 5. Remarquez que les maxima deviennent beaucoup plus nets ; plus le nombre de fentes par mètre est grand, mieux les maxima sont définis.
La diffraction de la lumière du cadmium ou du mercure est utilisée pour déterminer la séparation de deux lignes sur un circuit intégré. Les résultats suivants ont été obtenus pour les images diffractées de second ordre pour différentes longueurs d’onde. Utilisez-les pour tracer un graphique linéaire approprié et ainsi déterminer l’espacement moyen des fils sur le circuit.
| Longueur d’onde/nm | Angle de diffraction (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40,0 |
.