Heading

Le modèle d’espace d’état d’un système linéaire invariant dans le temps (LTI) peut être représenté comme suit ,

$\dot{X}=AX+BU$

$Y=CX+DU$

La première et la deuxième équation sont connues comme l’équation d’état et l’équation de sortie respectivement.

Où,

• X et $\dot{X}$ sont respectivement le vecteur d’état et le vecteur d’état différentiel.

• U et Y sont respectivement le vecteur d’entrée et le vecteur de sortie.

• A est la matrice du système.

• B et C sont les matrices d’entrée et de sortie.

• D est la matrice de feed-forward.

Concepts de base du modèle State Space

La terminologie de base suivante est impliquée dans ce chapitre.

State

C’est un groupe de variables, qui résume l’histoire du système afin de prédire les valeurs futures (sorties).

Variable d’état

Le nombre de variables d’état nécessaires est égal au nombre d’éléments de stockage présents dans le système.

Exemples – courant circulant dans l’inducteur, tension aux bornes du condensateur

Vecteur d’état

C’est un vecteur, qui contient les variables d’état comme éléments.

Dans les chapitres précédents, nous avons abordé deux modèles mathématiques des systèmes de contrôle. Il s’agit du modèle d’équation différentielle et du modèle de fonction de transfert. Le modèle d’espace d’état peut être obtenu à partir de l’un de ces deux modèles mathématiques. Discutons maintenant ces deux méthodes une par une.

Modèle d’espace d’état à partir de l’équation différentielle

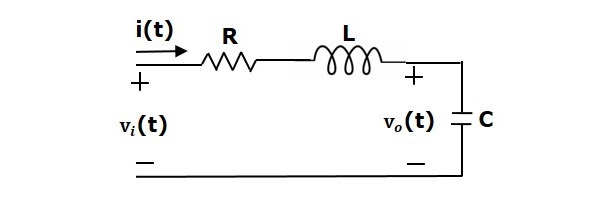
Il y a deux éléments de stockage (inducteur et condensateur) dans ce circuit. Ainsi, le nombre de variables d’état est égal à deux et ces variables d’état sont le courant traversant l’inducteur, $i(t)$ et la tension aux bornes du condensateur, $v_c(t)$.

Dans le circuit, la tension de sortie, $v_0(t)$ est égale à la tension aux bornes du condensateur, $v_c(t)$.

$v_0(t)=v_c(t)$

Appliquer le KVL autour de la boucle.

$v_i(t)=Ri(t)+L\frac{\text{\c}i(t)}{\text{\c}t}+v_c(t)$

$Flèche droite \frac{\c}{\c}i(t)}{\c}=-\frac{Ri(t)}{L}-\frac{v_c(t)}{L}+\frac{v_i(t)}{L}$

La tension aux bornes du condensateur est –

$v_c(t)=\frac{1}{C} \int i(t) dt$

Différencier l’équation ci-dessus par rapport au temps.

$\frac{\text{d}v_c(t)}{\text{d}t}=\frac{i(t)}{C}$

Vecteur d’état, $X=\begin{bmatrix}i(t) \\v_c(t) \end{bmatrix}$

Vecteur d’état différentiel, $\dot{X}=\begin{bmatrix}\frac{\text{d}i(t)}{\text{d}t} \\\frac{\text{d}v_c(t)}{\text{d}t} \end{bmatrix}$

Nous pouvons arranger les équations différentielles et l’équation de sortie dans la forme standard du modèle d’espace d’état comme,

$Y=\begin{bmatrix}0 & 1 \end{bmatrix}\begin{bmatrix}i(t) \v_c(t) \end{bmatrix}$

Où,

Modèle d’espace d’état à partir de la fonction de transfert

Considérons les deux types de fonctions de transfert en fonction du type de termes présents dans le numérateur.

• Fonction de transfert ayant un terme constant au numérateur.
• Fonction de transfert ayant une fonction polynomiale de ‘s’ au numérateur.

Fonction de transfert ayant un terme constant au numérateur

Considérons la fonction de transfert suivante d’un système

$\frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+….+a_1s+a_0}$

Réarrangez, l’équation ci-dessus sous la forme

$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$

Appliquez la transformée de Laplace inverse sur les deux côtés.

$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\frac{\text{d}y(t)}{\text{d}t}+a_0y(t)=b_0 u(t)$

Let

$y(t)=x_1$

.

$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$

$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$

$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$

$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$

and $u(t)=u$

Then,

$\dot{x}_n+a_{n-1}x_n+..+a_1x_2+a_0x_1=b_0 u$

À partir de l’équation ci-dessus, nous pouvons écrire l’équation d’état suivante.

$\dot{x}_n=-a_0x_1-a_1x_2-….-a_{n-1}x_n+b_0 u$

L’équation de sortie est –

$y(t)=y=x_1$

Le modèle d’espace d’état est -.

$\dot{X}=\begin{bmatrix}\dot{x}_1 \\dot{x}_2 \\\vdots \\\\dot{x}_{n-1} \\\dot{x}_n \end{bmatrix}$

$Y=\begin{bmatrix}1 && \dotso && 0 \end{bmatrix}\begin{bmatrix}x_1 \\\\\\x_2 \\\\vdots \x_{n-1} \\x_n \end{bmatrix}$

Ici, $D=\left .$

Exemple

Trouver le modèle d’espace d’état pour le système ayant une fonction de transfert.

$\frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}$

Réorganiser, l’équation ci-dessus comme,

$(s^2+s+1)Y(s)=U(s)$

Appliquer la transformée de Laplace inverse sur les deux côtés.

$\frac{\text{\d}^2y(t)}{\text{\d}t^2}+\frac{\text{\d}y(t)}{\text{\d}t}+y(t)=u(t)$

Let

$y(t)=x_1$

${\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$

et $u(t)=u$

Alors, l’équation d’état est

$\dot{x}_2=-x_1-x_2+u$

L’équation de sortie est

$y(t)=y=x_1$

Le modèle d’espace d’état est

$Y=\begin{bmatrix}1 & 0 \end{bmatrix}\begin{bmatrix}x_1 \\x_2 \end{bmatrix}$

Fonction de transfert ayant une fonction polynomiale de ‘s’ au numérateur

Considérons la fonction de transfert suivante d’un système

$\frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$

$\Flèche droite \frac{Y(s)}{U(s)}=\left( \frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0} \right )(b_n s^n+b_{n-1}s^{n-1}+…..+b_1s+b_0)$

L’équation ci-dessus se présente sous la forme d’un produit des fonctions de transfert de deux blocs, qui sont mis en cascade.

$\frac{Y(s)}{U(s)}=\left(\frac{V(s)}{U(s)}. \right ) \left(\frac{Y(s)}{V(s)}

Ici,

$\frac{V(s)}{U(s)}=\frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$

Réorganiser, l’équation ci-dessus comme

$(s^n+a_{n-1}s^{n-1}+….+a_0)V(s)=U(s)$

Appliquer la transformée de Laplace inverse sur les deux côtés.

$\frac{\text{d}^nv(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+a_1 \frac{\text{d}v(t)}{\text{d}t}+a_0v(t)=u(t)$

Let

$v(t)=x_1$

$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$

$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$

$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$

$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$

and $u(t)=u$

Then, l’équation d’état est

$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$

Consider,

$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$

Réorganiser, l’équation ci-dessus comme

$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$

Appliquer la transformée de Laplace inverse sur les deux côtés.

$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1\frac{\text{d}v(t)}{\text{d}t}+b_0v(t)$

En substituant les variables d’état et $y(t)=y$ dans l’équation ci-dessus, obtiendra l’équation de sortie comme,

$y=b_n\dot{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$

Substituer, la valeur $\dot{x}_n$ dans l’équation ci-dessus.

$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$

$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$

Le modèle d’espace d’état est

$\dot{X}=\begin{bmatrix}\dot{x}_1 \\\dot{x}_2 \\\\vdots \\\\dot{x}_{n-1} \\\\\dot{x}_n \end{bmatrix}$

$Y=\begin{bmatrix}x_1 \x_2 \\\\\vdots \x_{n-1} \x_n \end{bmatrix}$

Si $b_n = 0$, alors,

$Y=\begin{bmatrix}x_1 \\\x_2 \\\\\vdots \\x_{n-1} \end{bmatrix}$

.