La méthode des multiplicateurs de Lagrange est le cheval de bataille de l’économiste pour résoudre les problèmes d’optimisation. La technique est une pièce maîtresse de la théorie économique, mais malheureusement, elle est généralement mal enseignée.
La plupart des manuels se concentrent sur le fait de gruger mécaniquement des formules, laissant les étudiants mystifiés sur la raison pour laquelle cela fonctionne réellement pour commencer. Dans ce post, je vais expliquer une façon simple de voir pourquoi les multiplicateurs de Lagrange font réellement ce qu’ils font – c’est-à-dire résoudre des problèmes d’optimisation sous contrainte par l’utilisation d’une fonction lagrangienne semi-mystérieuse.
Un peu de contexte
Avant de voir pourquoi la méthode fonctionne, vous devez savoir quelque chose sur les gradients. Pour les fonctions d’une variable, il y a – généralement – une dérivée première. Pour les fonctions de n variables, il y a n dérivées premières. Un gradient est juste un vecteur qui rassemble toutes les dérivées premières partielles de la fonction en un seul endroit.
Chaque élément du gradient est une des dérivées premières partielles de la fonction. Une façon simple de penser à un gradient est que si nous choisissons un point sur une certaine fonction, cela nous donne la » direction » vers laquelle se dirige la fonction. Si notre fonction est étiquetée
la notation du gradient de f est
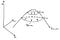
La chose la plus importante à savoir sur les gradients est qu’ils pointent toujours dans la direction de la plus forte pente d’une fonction en un point donné. Pour illustrer cela, regardez le dessin ci-dessous. Il illustre le fonctionnement des gradients pour une fonction à deux variables de x1 et x2.
La fonction f du dessin forme une colline. Vers le sommet, j’ai dessiné deux régions où nous maintenons la hauteur de f constante à un certain niveau a. On appelle ces régions des courbes de niveau de f, et elles sont marquées f = a1, et f = a2.
.
Imaginez-vous debout sur l’une de ces courbes de niveau. Pensez à un sentier de randonnée sur le flanc d’une montagne. Debout sur le sentier, dans quelle direction la montagne est-elle la plus abrupte ? Il est clair que la direction la plus abrupte est celle qui va directement vers le haut de la colline, perpendiculairement au sentier. Sur le dessin, ces chemins d’ascension les plus raides sont marqués par des flèches. Ce sont les pentes
à divers endroits des courbes de niveau. De même que la randonnée la plus raide est toujours perpendiculaire à notre sentier, les pentes de f sont toujours perpendiculaires à ses courbes de niveau.
C’est l’idée clé ici : les courbes de niveau sont là où
.
et
.
Comment fonctionne la méthode
Pour voir comment fonctionnent les multiplicateurs de Lagrange, jetez un coup d’oeil au dessin ci-dessous. J’ai redessiné la fonction f ci-dessus, ainsi qu’une contrainte g = c. Dans le dessin, la contrainte est un plan qui coupe notre colline. J’ai également dessiné quelques courbes de niveau de f.

.
Notre objectif ici est de monter le plus haut possible sur la colline, étant donné que nous ne pouvons pas nous déplacer plus haut que là où la contrainte g = c coupe la colline.
Dans le dessin, la frontière où la contrainte coupe la fonction est marquée par une ligne lourde. Le long de cette ligne se trouvent les points les plus élevés que nous pouvons atteindre sans enjamber notre contrainte. C’est un endroit évident pour commencer à chercher un maximum contraint.
Imaginez une randonnée de gauche à droite sur la ligne de contrainte. En prenant de l’altitude, nous passons par diverses courbes de niveau de f. J’en ai marqué deux sur l’image. À chaque courbe de niveau, imaginez vérifier sa pente – c’est-à-dire la pente d’une ligne tangente à celle-ci – et la comparer à la pente sur la contrainte où nous nous trouvons.
Si notre pente est supérieure à la courbe de niveau, nous pouvons atteindre un point plus élevé de la colline si nous continuons à avancer vers la droite. Si notre pente est inférieure à la courbe de niveau – disons, vers la droite où notre ligne de contrainte est en déclin – nous devons reculer vers la gauche pour atteindre un point plus élevé.
Lorsque nous atteignons un point où la pente de la ligne de contrainte est juste égale à la pente de la courbe de niveau, nous nous sommes déplacés aussi haut que possible. C’est-à-dire que nous avons atteint notre maximum contraint. Tout mouvement à partir de ce point nous fera descendre. Sur la figure, ce point est marqué par une grande flèche pointant vers le pic.
À ce point, la courbe de niveau f = a2 et la contrainte ont la même pente. Cela signifie qu’elles sont parallèles et pointent dans la même direction. Mais comme nous l’avons vu plus haut, les pentes sont toujours perpendiculaires aux courbes de niveau. Donc, si ces deux courbes sont parallèles, leurs gradients doivent également être parallèles.
Cela signifie que les gradients de f et g pointent tous deux dans la même direction, et diffèrent au maximum par un scalaire. Appelons ce scalaire « lambda ». Nous avons alors,
Solvant pour zéro, nous obtenons
C’est la condition qui doit être vérifiée lorsque nous avons atteint le maximum de f soumis à la contrainte g = c. Maintenant, si nous sommes intelligents, nous pouvons écrire une seule équation qui capturera cette idée. C’est là qu’intervient l’équation lagrangienne familière :
ou plus explicitement ,
Pour voir comment cette équation fonctionne, regardez ce qui se passe lorsque nous suivons la procédure lagrangienne habituelle. Tout d’abord, nous trouvons les trois dérivées premières partielles de L,
.
et les fixer à zéro. Autrement dit, il faut que le gradient de L soit égal à zéro. Pour trouver le gradient de L, nous prenons les trois dérivées partielles de L par rapport à x1, x2 et lambda. Puis nous plaçons chacune d’elles comme élément d’un vecteur 3 x 1. Cela nous donne ce qui suit :
.
Rappelons que nous avons deux « règles » à suivre ici. Premièrement, les gradients de f et g doivent pointer dans la même direction, or
Et deuxièmement, nous devons satisfaire notre contrainte, soit
.
Les premier et deuxième éléments du dégradé de L permettent de s’assurer que la première règle est respectée. A savoir , ils forcent
.
assurant que les gradients de f et g pointent tous deux dans la même direction. Le troisième élément du gradient de L est simplement une astuce pour s’assurer que g = c, qui est notre contrainte. Dans la fonction lagrangienne, lorsque nous prenons la dérivée partielle par rapport à lambda, cela nous renvoie simplement notre équation de contrainte originale.
À ce stade, nous avons trois équations en trois inconnues. Nous pouvons donc résoudre cela pour les valeurs optimales de x1 et x2 qui maximisent f sous réserve de notre contrainte. Et nous avons terminé.
Donc, l’essentiel est que les multiplicateurs de Lagrange ne sont en fait qu’un algorithme qui trouve où le gradient d’une fonction pointe dans la même direction que les gradients de ses contraintes, tout en satisfaisant également ces contraintes.
Comme dans la plupart des domaines des mathématiques, une fois que vous voyez le fond des choses – dans ce cas, que l’optimisation n’est en fait que de l’escalade de colline, ce que tout le monde comprend – les choses sont beaucoup plus simples que ce que la plupart des économistes les font paraître.