星の全体的な寿命は、その質量によって決まります。
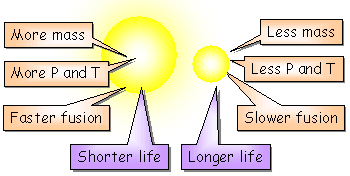
大質量の星は、重力崩壊から身を守るために、より高い中心温度と圧力を必要とするため、核融合反応が低質量の星よりも速い速度で進行します。 その結果、質量の大きい星は、核となる水素を急速に使い果たし、赤色巨星に進化するまでの主系列の時間が短くなる。
主系列の寿命を表す式は、恒星の質量の関数として得ることができ、通常は太陽単位の関係で書かれます(この式の導出については以下を参照してください)。
![]()
| where | t⊙ | = | Sun MS lifetime = 1010 |
| M | = | 星の質量 | |
| M⊙ | = | 太陽質量 |
したがって、主系列星の寿命は、40太陽質量のO-型星では100万年、40太陽質量のO-型星では100万年となります。型の星で100万年、0, 0.2太陽質量のM型星では5600億年です。2太陽質量のM型星では5600億年となります。 宇宙の年齢が137億年しかないことを考えると、M型星の主系列の寿命が長いということは、これまでに生まれたすべてのM型星がまだ主系列にあるということになります。
演繹法
星の明るさは、単位時間あたりに放出されるエネルギーの量です。 主系列星の場合、そのエネルギーは水素の核融合によるもので、次のようになります。
L = E/t
| ここで | L | = | 星の光度 |
| E | E | = | Hの燃焼によって生成されるエネルギー |
| t | = | 時間 |
アインシュタインのエネルギー-質量方程式を使って、Hの燃焼によって生成されるエネルギーを計算することができます。質量の式を使って、水素の燃焼で発生するエネルギーを計算することができます。 燃焼によってエネルギーに変換される質量は、星の全質量の何分の一かになります。
E = f M c2 where
| where | E | = | Hの燃焼によって生成されるエネルギー |
| f | = | 質量の割合 エネルギーに変換される | |
| M | = | 星の質量 | |
| c | = | 光の速さ |
最後の2つの式を組み合わせます。 主系列の寿命を表す以下の式が得られます。
tMS ∼ M/L
主系列星の質量-光合成の関係を用いて:
L ∼ M3.5
Lを代入すると、主系列星の寿命を恒星の質量で表した式が得られます:
tMS ∼ M-2.5
これは太陽単位で表すことができます:
![]()
| where | t⊙ | = | Sun MS lifetime = 1010 |
| M | = | 星の質量 | |
| M⊙ | = | 太陽質量 |
注意。 この式は近似的なものであり、非常に重い星や非常に軽い星には有効ではありません。 主な制限は、主系列星の単一値の質量-光度関係を使用することです。