線形時不変(LTI)システムの状態空間モデルは次のように表すことができます。
$$dot{X}=AX+BU$
$Y=CX+DU$
第1式を状態方程式、第2式を出力方程式と呼びます。
ここで、
-
Xおよび$\dot{X}$は、それぞれ状態ベクトルおよび微分状態ベクトルです。
-
UとYはそれぞれ入力ベクトルと出力ベクトルです。
-
Aはシステム行列です。
-
BとCは入力行列と出力行列です。
-
D はフィードフォワード行列です。
Basic Concepts of State Space Model
この章では、以下の基本的な用語を説明します。
状態変数
必要な状態変数の数は、システムに存在する記憶要素の数と同じです。
例 – インダクタに流れる電流、コンデンサにかかる電圧
状態ベクトル
状態変数を要素として含むベクトルです。 それは、微分方程式モデルと伝達関数モデルです。 状態空間モデルは、これらの2つの数学的モデルのいずれかから得ることができます。
微分方程式からの状態空間モデル
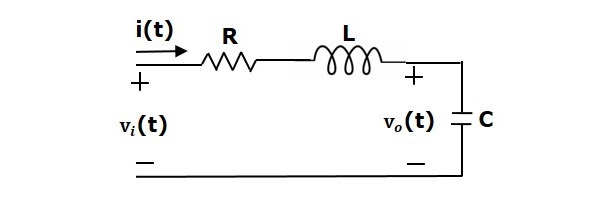
この回路には2つの記憶素子(インダクタとコンデンサ)があります。
この回路から出力される電圧$v_0(t)$は、コンデンサにかかる電圧$v_c(t)$と等しくなります。
$v_0(t)=v_c(t)$
ループの周りにKVLを適用します。
$v_i(t)=Ri(t)+L\frac{\{d}i(t)}{text{d}t}+v_c(t)$
$$\\{d}i(t)}{\{d}t}=-。\¶Ri(t)}{L}- ¶v_c(t)}{L}+ ¶v_i(t)}{L}$
コンデンサにかかる電圧は –
$v_c(t)=¶frac{1}{C} \dt$
上の式を時間に対して微分すると、次のようになります。
$frac{\\{d}v_c(t)}{text\{d}t}=\frac{i(t)}{C}$
State vector, $X=\begin{bmatrix}i(t) \v_c(t) ╲end{bmatrix}$
微分状態ベクトル $dot{X}=\begin{bmatrix}\frac{text{d}i(t)}{\{d}t} です。 \\\frac{\text{d}v_c(t)}{\text{d}t}
これらの微分方程式と出力方程式は、状態空間モデルの標準的な形に整えることができます。
$Y=\begin{bmatrix}0 & 1 \begin{bmatrix}i(t) \v_c(t) ୨୧$
ここです。
Transfer FunctionからのState Space Model
分子に含まれる項の種類により、2種類のTransfer Functionを考えます。
- 分子に一定の項を持つ伝達関数
- 分子に「s」の多項式関数を持つ伝達関数。
分子に定数項を持つ伝達関数
次のようなシステムの伝達関数を考えてみましょう
$frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+…。+a_1s+a_0}$
上の式を次のように再整理します
$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$
両辺に逆ラプラス変換を施します。
$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\\{\{d}y(t)}{\{d}t}+a_0y(t)=b_0 u(t)$$
Let
$y(t)=x_1$
$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then,
$\dot{x}_n+a_{n-1}x_n+….+a_1x_2+a_0x_1=b_0 u$
上の式から、次の状態方程式が書けます。-a_{n-1}x_n+b_0 u$
出力方程式は-
$y(t)=y=x_1$
状態空間モデルは-。
$\dot{X}=\begin{bmatrix}\{x}_1 ୨୧{x}_2 ୨୧{n-11} ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ ! \0 & 0 end{bmatrix}\begin{bmatrix}x_1 ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˶‾᷅˵ ˵1} ¶¶n ¶end{bmatrix}$
ここでは D=レフト。$
Example
伝達関数を持つシステムの状態空間モデルを求めます。
$frac{Y(s)}{U(s)}=\frac{1}{s^2+s+1}$
上の式を次のように再配列してください。
$frac{\{d}^2y(t)}{\{d}t^2}+$frac{\{d}y(t)}{\{d}t}+y(t)=u(t)$
Let
以下のようになります。
$y(t)=x_1$
$frac{\\{d}y(t)}{text{d}t}=x_2=\dot{x}_1$
そして$u(t)=u$
すると。 状態方程式は次のようになります
$\\{x}_2=-x_1-.x_2+u$
出力方程式は
$y(t)=y=x_1$
状態空間モデルは
$Y=\begin{bmatrix}1 & 0 ୨୧{bmatrix}x_1 ୨୧{bmatrix}x_2
分子にsの多項式関数を持つ伝達関数
次のようなシステムの伝達関数を考えてみましょう。1}s^{n-1}+….+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
$Rightarrow \frac{Y(s)}{U(s)}=left( ˶ˆ꒳ˆ˵ )(b_n s^n+b_{n-1}s^{n-1}+…+a_1 s+a_0} ˶ˆ꒳ˆ˵ )(b_n s^n+b_{n-1}s^{n-1}+…+b_1 s+a_0).+b_1s+b_0)$
上の式は、カスケード接続された2つのブロックの伝達関数の積の形をしています。
$frac\{Y(s)}{U(s)}=\left(˶‾᷄ -̫ ‾᷅˵) \right ) \\\\ ここで、
$\\{V(s)}{U(s)}=\\{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$
上の式を次のようにアレンジしてください
$(s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$
両辺に逆ラプラス変換を適用します
$$frac{\\{d}^nv(t)}{text{d}t^n}+a_{n-1}\{d}^{n-1}v(t)}{text{d}t^{n-1}+…+a_1 ¶frac{text{d}v(t)}{\text{d}t}+a_0v(t)=u(t)$$
Let
$v(t)=x_1$
$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then, 状態方程式は
$\\{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$
Consider,
$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
上の式を次のように再整理します
$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
両辺に逆ラプラス変換を施します。
$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1_frac{\{d}v(t)}{\{d}t}+b_0v(t)$
上の式に状態変数と$y(t)=y$を代入すると、出力式は次のようになります
$y=b_n\{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$
上の式に$dot{x}_n$の値を代入すると、
$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$
$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$
状態空間モデルは
$dot{X}=\begin{bmatrix}\{x}_1 ˶‾᷄덴덴덴덴덴덴덴덴덴}です。1} ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━.
$Y=\\\\\\\\\\\\\\\\⁾⁾