学習目標
このセクションの終わりには、以下のことができるようになります。

図1。 消される幸せな顔の量は、点Aと点Bの間で消しゴムがたどる経路と、摩擦に対して行われる仕事に依存します。 (a)の経路では、(b)の経路に比べて仕事量が少なく、顔が消される量も少なくなります。 ここでの力は摩擦であり、仕事のほとんどは熱エネルギーとなってシステムから出ていきます(幸せな顔と消しゴム)。
非保存的な力が機械的エネルギーに与える影響
非保存的な力が作用すると、機械的エネルギーが保存されないことがあります。 例えば、自動車が平地で摩擦により停止した場合、運動エネルギーが失われ、そのエネルギーは熱エネルギーとして放散され、機械的エネルギーが減少します。 図2は、保存的な力と非保存的な力の効果を比較したものです。

仕事エネルギーの定理はどのように適用されるか
さて、保存的な力と非保存的な力の両方が作用する場合、仕事エネルギーの定理はどのような形になるか考えてみましょう。 非保存的な力によってもたらされる仕事は、システムの力学的エネルギーの変化に等しいことがわかります。 運動エネルギーと仕事エネルギーの定理」で述べたように、仕事エネルギーの定理では、系の正味仕事はその運動エネルギーの変化に等しい、つまりWnet = ΔKEとなります。 この正味の仕事は、非保存的な力による仕事と保存的な力による仕事の合計です。 つまり、
Wnet = Wnc + Wc,
だから
Wnc + Wc = ΔKE,
ここで、Wncはすべての非保守的な力によって行われた仕事の合計であり、Wcはすべての保守的な力によって行われた仕事の合計です。

図3. 人が木箱を押してスロープを登り、木箱に仕事をしています。 摩擦と重力(図示せず)も木箱に仕事をしますが、この2つの力は人の押しに反対します。
図3は、人が木箱を押してスロープを登り、摩擦で反対されている状態を示しています。 前節と同様に、保存的な力による仕事は重力位置エネルギーの損失から生じるので、Wc = -ΔPEとなります。 この式を前の式に代入してWncを解くと、
Wnc = ΔKE + ΔPE.
この式は、総機械エネルギー(KE + PE)が、非保存的な力によって行われた仕事の量だけ変化することを意味します。
この式は、総機械エネルギー(KE + PE)が、非保存的な力による仕事の分だけ変化することを意味します。 したがって、対象となるシステム(木箱など)でエネルギーが保存されていなくても、総機械エネルギーの変化を引き起こすために同量の仕事が行われたことがわかります。
Wnc = ΔKE + ΔPEを再整理すると
KEi + PEi + Wnc = KEf + PEfが得られます。
これは、非保存的な力によって行われた仕事の量は、システムの機械的エネルギーに追加されることを意味します。 Wncが正であれば、図3の人が木箱を押してスロープを上るときのように、力学的エネルギーが増加します。 Wncが負であれば、図2bの石が地面に当たったときのように、力学的エネルギーが減少します。 Wncがゼロであれば、力学的エネルギーは保存され、非保存的な力は均衡します。 例えば、平地で芝刈り機を一定の速度で押すと、自分が行った仕事は摩擦の仕事によって取り除かれ、芝刈り機のエネルギーは一定になります。
Applying Energy Conservation with Nonconservative Forces
位置エネルギーの変化が起こらない場合、KEi + PEi + Wnc = KEf + PEf を適用することは、運動エネルギーの変化をシステムに加えられた正味の仕事と等しくすることで、仕事エネルギー定理を適用することになります。 しかし、位置エネルギーと運動エネルギーの両方の変化を伴う状況で、代わりに合計機械エネルギーの変化を求めようとする場合、前の式 KE i + PEi + Wnc = KEf + PEf は、位置エネルギーの変化を含む保存的な力だけによって生じたであろう機械エネルギーの変化を求めることから始めて、それに関係する非保存的な力によって行われた仕事を適切な符号で加えることができることを示しています。
Example 1. 移動した距離を計算する。 野球選手が滑る距離
図4に示すように、野球選手が平地で滑って止まるという状況を考えます。

。
戦略
摩擦は、プレーヤーの運動エネルギーを熱エネルギーを含む他の形態に変換することによってプレーヤーを停止させます。 仕事とエネルギーの定理の観点から、摩擦によってもたらされる仕事は負の値であり、初期の運動エネルギーに加えられてゼロになります。 摩擦による仕事は、fが運動の反対方向(つまりθ=180°なのでcosθ=-1)なので、負の値となる。 したがって、Wnc = -fdとなります。
\frac{1}{2}{mv_{text{i}}}^2-fd=0\\
or
fd=\frac{1}{2}{mv_{text{i}}}^2\\。
この式を距離dについて解くことができます。
解答
先ほどの式をdについて解き、既知の値を代入すると
egin{array}{lll}d
=&\frac{mv_{\text{i}}^2}{2f}\\\text{ }&&\frac{(65.0text{ kg})(6.00\{ m/s})^2}{(2)(450\{ N})}\{ }&&2.60\\\\\\\\\\\\\\\\\\\\\\\ 例えば、大きな機械的エネルギーを持つトラックを止めるためには、蚊を止めるためよりも努力しなければなりません。 移動距離の計算。 傾斜を滑る
例1の選手が、野球場と同じような表面を持つ、上方向に5.00°の傾斜を持つ丘を走っているとします。 プレイヤーは同じ初速で滑ります。

図5.
戦略
この場合、選手にかかる非保存的な摩擦力によって行われた仕事は、高さがゼロのときの運動エネルギーから、丘に沿って高さhに到達するために距離dを移動することで最終的に得られる機械的エネルギー(h = d sin 5.00º)まで、選手が持つ機械的エネルギーを減少させます。 これは、KE + PEi + Wnc = KE f + PEf という方程式で表されます。
解答
摩擦による仕事は再びWnc = -fdとなり、初期の位置エネルギーはPEi = mg – 0 = 0、運動エネルギーは\text{KE}_{\text{i}}=\frac{1}{2}mv_{\{i}}^2\となり、最終的なエネルギーの寄与は運動エネルギーがKEf = 0、位置エネルギーがPEf = mgh = mgd sin θとなります。
これらの値を代入すると
\frac{1}{2}{mv_{text{i}}}^2+0+\left(-)fd\\right)=0+mgd\sin\theta\
これをdについて解くと
\begin{array}{lll}d&=
\frac{\left(\frac{1}{2}\right)mv_{\text{i}}^2}{f+mg\sin\theta}\\&&\frac{(0.5)(65.0\\{ kg})(6.00\\{ m/s})^2}{450\\{ N}+(65.0\\{ kg})୨୧(9.80\{ m/s}^2)୨୧(5.00^^^^^^^^^^^^^)}&&2.
議論
予想通り、坂道を滑った方が短い距離を滑ることができました。 この問題は、位置エネルギーを使わずに、力と仕事エネルギーの定理を使って解くこともできます。 この方法では、法線方向の力と重力方向の力のベクトルが異なる方向を向いているために相殺されないことと、摩擦を組み合わせて、正味の力を求める必要がありました。 そして、その正味の力と正味の仕事を使って、運動エネルギーがゼロになる距離dを求めることができます。 エネルギー保存を適用して、代わりに位置エネルギーを使うことで、力のベクトルを組み合わせて解決することなく、重力の位置エネルギーmghだけを考えればよいことになります。
Making Connections: Take-Home Investigation-Determining Friction from the Stopping Distance
この実験では、重力位置エネルギーを熱エネルギーに変換します。 重力ポテンシャル エネルギーの「Making Connections」のセクションにある定規、本、ビー玉を使用します。 また、図6のように側面に小さな穴の開いた発泡スチロールのカップも用意します。 定規の10cmの位置から、ビー玉を定規の下にあるカップの中に転がします。 カップが止まるまでの距離dを測ります。 どのような力で止まったのでしょうか? 定規の下にあるビー玉の運動エネルギーはどうなりましたか? 次に、ビー玉を20cmと30cmの位置に置き、ビー玉がカップに入った後のカップの移動距離を再び測ります。 カップの移動距離と定規上のビー玉の初期位置をプロットします。
簡単な仮定のもとに、これらのデータを使って、テーブル上のカップの動摩擦係数μkを求めることができます。 カップにかかる摩擦力fはμkNで、法線力Nはカップの重さとビー玉の重さだけです。 法線力と重力は、水平方向に移動するコップの変位に対して垂直なので、仕事をしません。 摩擦によってもたらされる仕事はfdです。
上記の実験を、鉄製のビー玉(またはボールベアリング)でも行うと面白いです。 ガラス製のビー玉と同じ定規の位置からビー玉を離したとき、この鋼鉄製のビー玉の速度は、定規の底にあるビー玉の速度と同じですか?

PhET Explorations: タラップ
家庭にあるものをタラップで押し上げたり下げたりしながら、力、エネルギー、仕事について探ります。 傾斜路を下げたり上げたりして、傾斜の角度がファイルキャビネットに働く平行な力にどのように影響するかを確認します。
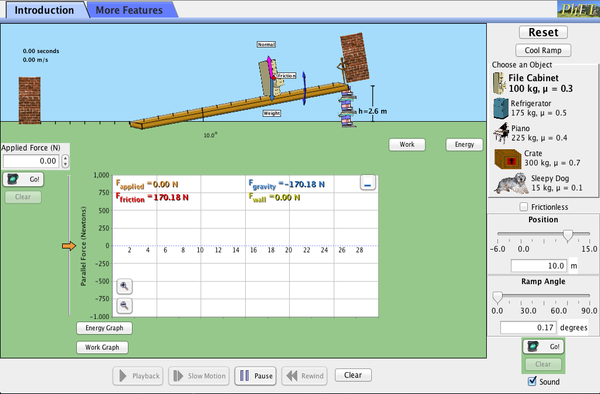
クリックするとダウンロードできます。
Section Summary
- 非保存的な力とは、仕事が経路に依存する力のことです。
- 摩擦は、機械的エネルギーを熱エネルギーに変える非保存的な力の一例です。
- 保存的な力と非保存的な力の両方が作用する場合、エネルギー保存が適用され、正味の力から正味の仕事を求めたり、ニュートンの法則を直接適用しなければならないのではなく、保存的な力の既知の位置エネルギーと非保存的な力によって行われる仕事の観点から運動を計算するために使用することができます。
問題集 & 演習
- 60.0kgのスキーヤーが初速12.0m/sで図7のような高さ2.50mの高台を惰性で登ります。 スキー板と雪の間の摩擦係数が0.0800であることを仮定して、頂上での最終速度を求めなさい。

図7.傾斜した斜面が終わった時点でのスキーヤーの最終速度は不明です。
- (a) 摩擦による仕事が無視でき、初速が110km/hの場合、自動車はどのくらいの高さの坂を惰性で上ることができるか(エンジンを切った状態)。 (b) 実際に、初速110km/hの750kgの車が、坂道をスタート地点から22.0mの高さまで惰性で登っていく様子が観察された場合、摩擦による熱エネルギーはどのくらい発生したか。 (c) 丘の傾斜が水平より2.5°の場合、摩擦の平均的な力は何ですか。
Glossary
非保存的な力:与えられた初期構成と最終構成の間でたどる経路に仕事が依存する力
摩擦。 摩擦は機械的エネルギーを熱エネルギーに変える
選択された問題の解答 & 演習
1. 9.46m/s
2.