ラグランジュ乗数法は、最適化問題を解決するための経済学者の主力となる手法です。
ほとんどの教科書では、機械的に数式を書き出すことに重点が置かれており、学生はそもそもなぜラグランジュ乗法が有効なのかを理解できないままになっています。
いくつかの背景
この方法がなぜ機能するかを理解する前に、勾配について知っておく必要があります。 1変数の関数には、通常、1つの1次導関数があります。 n個の変数の関数の場合、n個の1次導関数があります。
勾配の各要素は、関数の部分的な 1 次導関数の 1 つです。 勾配を簡単に考える方法は、ある関数上の点を選ぶと、その関数が向かっている「方向」がわかるということです。 関数にラベルが付いている場合
fの勾配の表記は
勾配について知っておくべき最も重要なことは、勾配は常に与えられた点における関数の最も急な傾きの方向を向いているということです。 これを説明するために、以下の図を見てください。
図中の関数 f は丘を形成しています。 これらは f の水準曲線と呼ばれ、f = a1、f = a2 と記されています。
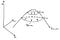
となります。
自分がそのような水平なカーブの上に立っていることを想像してみてください。 山の中腹にあるハイキングコースを思い浮かべてみてください。 登山道に立って、山が一番険しいのはどの方向でしょうか? 明らかに最も急な方向は、登山道と垂直にまっすぐ登っていく方向です。 図面では、これらの最も急な上り坂の道が矢印で示されています。 これが勾配です
レベルカーブに沿って様々なポイントで。 最も急なハイキングコースが常に私たちのトレイルに垂直であるように、fの勾配は常にその水平曲線に垂直です。
これがここでの重要なアイデアです。 レベルカーブとは
のことです。
and
この手法の仕組み
ラグランジュ乗法の仕組みを見るには、以下の図をご覧ください。 下の図を見てください。 上から関数fと制約g=cを描き直しました。この図では、制約は丘陵を横切る平面です。 また、f の水平な曲線を 2 つ描いています。

div
ここでの私たちの目標は、丘の上にできるだけ高く登ることです。 制約 g = c が丘を切断する場所よりも高く移動することはできません。
図では、制約が関数を切断する境界が太い線で示されています。 その線に沿って、制約を越えることなく到達できる最高点があります。
制約線上を左から右に向かって歩くことを想像してみてください。 高さが増すにつれて、f のさまざまなレベル曲線を通過します。
もし、傾きがレベルカーブより大きければ、右に進めば丘の上のより高いところに到達できることになります。
傾きがレベル曲線よりも大きい場合、右に移動し続ければ、丘の上のより高いポイントに到達できます。
制約線の傾きがレベル曲線の傾きとちょうど等しくなるポイントに到達すると、できる限り高く移動したことになります。 つまり、制約された最大値に達したということです。 そこから先の動きは、坂道を下ることになります。
その時点で、レベル曲線 f = a2 と拘束条件は同じ傾きを持っています。 つまり、平行で同じ方向を向いているということです。 しかし、上で見たように、勾配は常にレベルカーブに垂直です。
つまり、f と g の勾配はどちらも同じ方向を向いていて、最大でもスカラー分だけ異なるということです。 そのスカラーを “lambda “と呼びましょう。
ゼロについて解くと、以下のようになります。
これは、g=cという制約の下でfの最大値に達したときに成立する条件です。 さて、うまくすれば、この考えを表現する1つの方程式を書くことができます。 ここで、おなじみのラグランジュ方程式の出番です。
あるいはもっと明確に。
この式がどのように機能するかを見るために。 通常のラグランジュの手順に従うとどうなるかを見てみましょう。 まず、Lの3つの偏1次導関数を求めます。
iv
そして、それらをゼロに設定します。 つまり、Lのグラデーションをゼロにする必要があります。 Lの勾配を求めるには、x1、x2、lambdaに対するLの3つの偏微分を取ります。 そして、それぞれを3×1のベクトルの1要素として配置する。 すると次のようになります。
となります。
ここでは、2つの「ルール」があることを思い出してください。 まず、fとgのグラデーションが同じ方向を向いていなければなりません。 or
そして2つ目は、制約条件を満たさなければなりません。 または
となります。
Lのグラデーションの1つ目と2つ目の要素は、1つ目のルールが守られていることを確認しています。 それは
div
fとgのグラデーションがともに同じ方向を向いていることを確認します。 L の勾配の 3 番目の要素は、我々の制約である g = c を確認するための単なるトリックです。 ラグランジュ関数では、ラムダに関する偏微分を取ると、元の制約式に戻るだけです。
この時点で、3 つの未知数に対する 3 つの方程式があります。 そこで、制約のもとで f を最大化する x1 および x2 の最適な値を求めて、これを解くことができます。
つまり、ラグランジュ乗数とは、関数の勾配が制約の勾配と同じ方向を向き、かつ制約を満たす場所を見つけるアルゴリズムに過ぎないということです。
数学のほとんどの分野と同様に、一度物事の本質を見極めれば (この場合、最適化とは誰もが理解している単なる丘登りであり、)、物事は多くの経済学者が考えているよりもはるかに単純です。