divide and conquer algorithmは、大きな問題を解決するための戦略で、
- 問題を小さなサブ問題に分解し、
- サブ問題を解決し、
- それらを組み合わせて目的の出力を得ることができます。
divide and conquer algorithmを使用するには、再帰が使用されます。
- Javaでの再帰
- Pythonでの再帰
- C++での再帰
How Divide and Conquer Algorithms Work?
以下のステップがあります:
- 分割。
- Conquer: 小さいサブ問題を再帰的に解きます。 サブプロブレムが十分小さい場合は、それを直接解きます。
- Combine:
例を挙げてこの概念を理解しましょう。
ここでは、分割統治法 (マージ ソート) を使用して配列をソートします。
- 与えられた配列を次のようにします:

マージソートのための配列 - 配列を2つに分割します。

配列を2つのサブパートに分割 さらに、個々の要素が得られるまで、各サブパートを再帰的に2つのハーフパートに分割します。
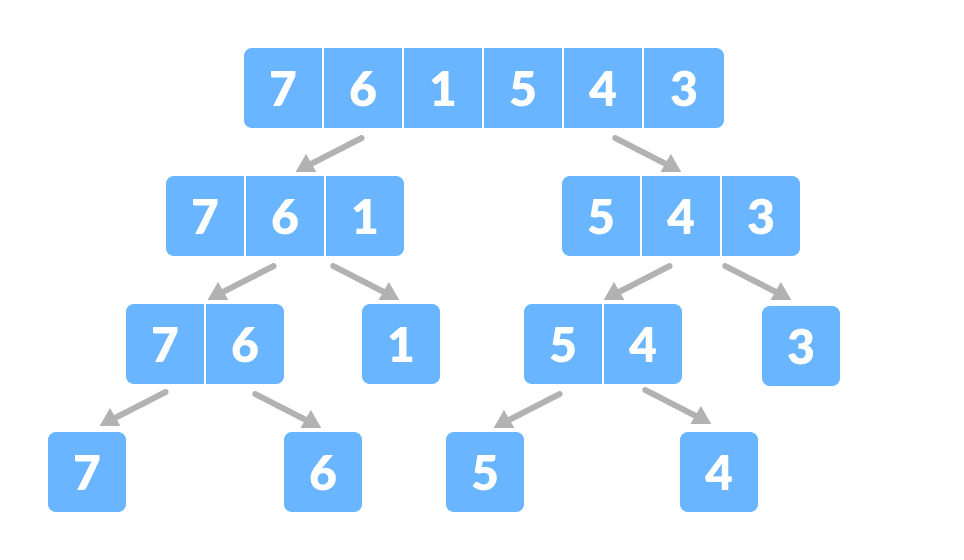
Divide the array into small subparts - さて、個々の要素を並べ替えて結合します。 ここでは、「征服」と「結合」のステップが並行して行われます。
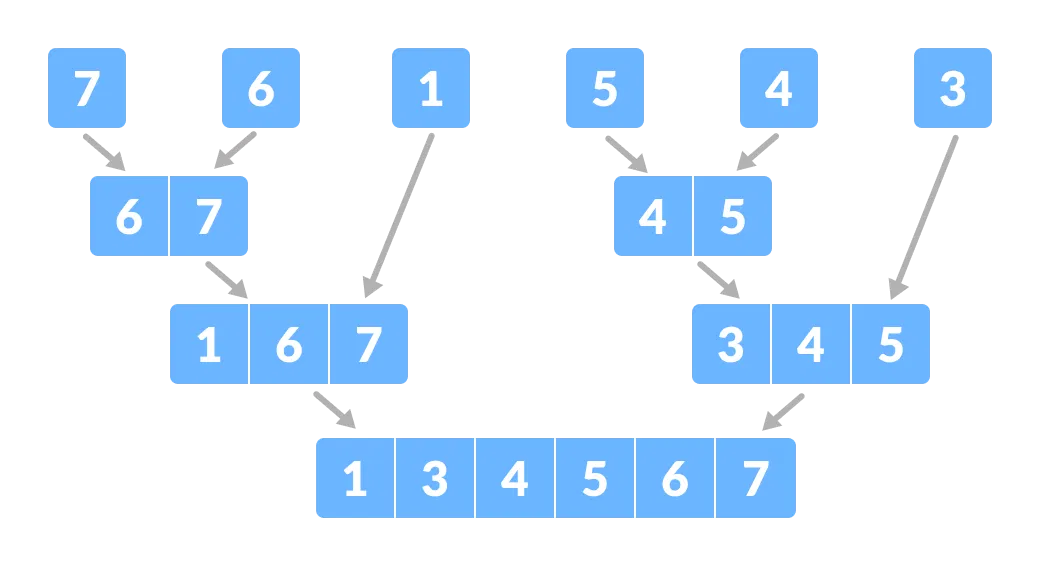
サブパーツを組み合わせる 。
時間的複雑さ
分割統治アルゴリズムの複雑さは、マスターの定理を使って計算されます。
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
再帰的な問題の時間的複雑さを求める例を見てみましょう。
マージソートの場合、式は次のように書くことができます。
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Divide and Conquer Vs Dynamic approach
Divide and Conquer approachは、問題をより小さなサブプロブレムに分割します。 これらの小問題はさらに再帰的に解決されます。
同一サブプロブレムを何度も解かない場合は、divide and conquer approachを使用します。
同じサブプロブレムを何度も解かない場合は、分割統治方式を使用し、サブプロブレムの結果を将来的に何度も使用する場合は、動的方式を使用します。 フィボナッチ級数を求めようとしているとします。
Divide and Conquer approach:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Dynamic approach:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
Dynamic approachでは、memは各サブプロブレムの結果を保存します。
Divide and Conquer Algorithm の利点
- 素朴な方法を使用した 2 つの行列の乗算の複雑さは O(n3) であるのに対し、Divide and Conquer アプローチ (すなわち Strassen の行列乗算) を使用すると O(n2.8074) となります。
- このアプローチはマルチプロセッシング システムに適しています。
- メモリ キャッシュを効率的に使用します。
Divide and Conquer Applications
- Binary Search
- Merge Sort
- Quick Sort
- Strassen’s Matrix Multiprication
- Karatsuba Algorithm



