ExcelでSLOPEを計算する

SLOPE関数は、既知のxと既知のyで作られる回帰直線の傾きを返します。

傾きの公式とは

数学的に言えば、直線の急峻さを表す数値です。傾きは、グラフ上の2点を結ぶ直線として視覚化できます。負の傾きは、直線が右下に向かっていることを意味します。正の傾きは、線がグラフの右側を上に向かっていることを示します。既知の x と既知の y の傾きを計算するための数式は、次のとおりです。

SLOPEの構文

=SLOPE(known_ys,known_xs)

known_ys:

known_ys: 既知のyの値

known_xs: 既知のxの値

注：xとyの観測値の数は同じである必要があります。

excelでSlopeを求める例を見てみましょう

Example: 既知の ys と xs で作成した回帰線の傾きを求める

ここでは、excel の SLOPE 関数の使い方を説明するために、小さなデータセットを用意しました。このデータには、範囲A2:A7の既知のxsと、範囲B2:B7の既知のysが含まれています。

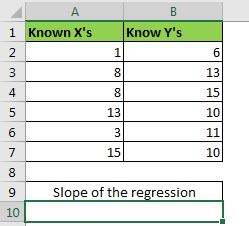セルA10に以下の式を書きます。

=SLOPE(B2:B7,A2:A7)

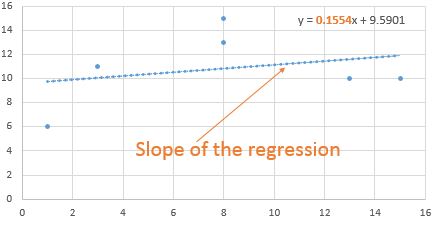
データの傾きは0.155405405となっています。

解釈：

傾きが0.16ということは、どういうことでしょうか？これは、xが1単位増加するごとに、yが0.16だけ増加することを意味しています。

また、傾きが正であることから、グラフの右側で上向きになっていることがわかります。

どのような仕組みになっているのでしょうか

どのようにして直線の傾きを得たのかを理解するには、数学を理解し、Excelの基本的な数学を使用して計算する必要があります。

データセットの傾きを手動で計算するには、傾きの数式をExcelの数式に変換する必要があります。 xとyの平均を計算するには、AVERAGE関数を使います。

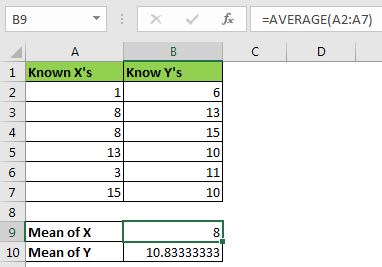セルB9に次のように書きます：

=AVERAGE(A2:A7)

セルB10に次のように書きます：

=AVERAGE(B2:B7)

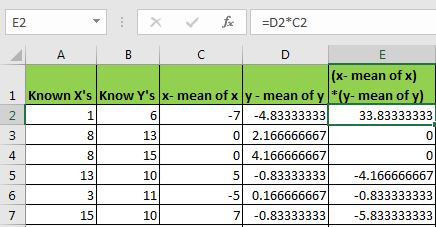
次に、各xとyの平均値の差を計算する必要があります。

=A2-$B$9

=B2-$B$10

ドラッグしてください。

次に、これらの差の積が必要です（上の式を参照）。 D2とC2を掛け合わせ、下にドラッグします。

次に、各xの二乗-xの平均を求めます（上記の数式を参照）。セルF2に、この数式を書いて下にドラッグします。

=POWER(C2,2)

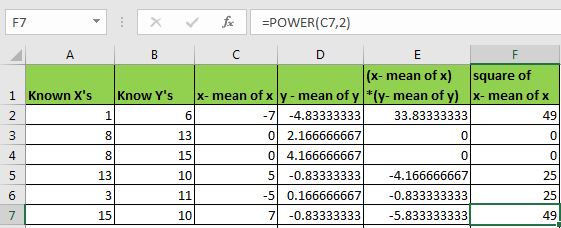ここで、範囲E2:E7とF2:F7を合計します（数式に従う）

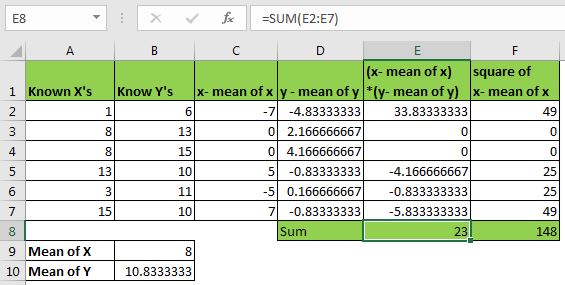これで、このデータのSLOPEを計算する準備が整いました。 (x-xの平均)*(y-yの平均)の合計をx-xの平均の2乗の合計で割るだけです。エクセルの言葉で言えば、E8をF8で割ることになります

セルA13に、この式を書きます。

=E8/F8

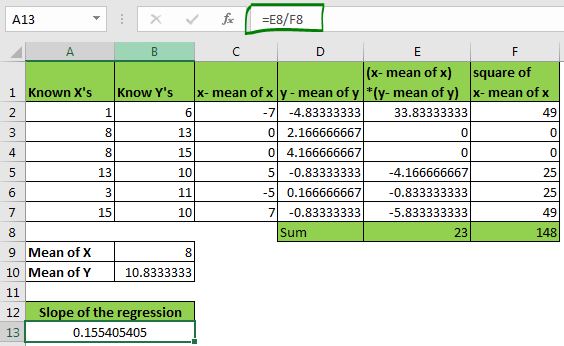
再びaur slopeの値が出てきました。SLOPE関数を使って確認してみてください。それらは同じです。唯一の違いは、疲れるプロセスでした。

そう、皆さん、これがエクセルのSLOPE関数の使い方です。お役に立てれば幸いです。

Heading