⇐ 前のトピック|次のトピック ⇒ 目次
実験を行う前に、求める効果を検出するために必要な観測値の数を見積もるために、検出力分析を行う必要があります。
はじめに
実験を計画する際には、必要なサンプルサイズを見積もることが良いでしょう。 これは、人間や他の脊椎動物に苦痛を与えることを提案している場合、個体数を最小限にすることが特に重要な場合 (サンプル サイズが小さすぎて、実験全体が時間と苦痛の無駄にならないように)、または非常に時間のかかる、または高価な実験を計画している場合に特に当てはまります。 特定の効果を検出するために必要なサンプルサイズを推定したり、特定のサンプルサイズで検出できる効果の大きさを推定したりする方法が、多くの統計的検定で開発されています。
検出力分析を行うためには、効果量を指定する必要があります。これは、帰無仮説と対立仮説の間にある、検出したい差の大きさを意味します。 応用研究や臨床生物学研究では、検出したい効果量がはっきりしている場合があります。 例えば、新しい犬用シャンプーをテストしている場合、会社のマーケティング部門は、犬の被毛が平均で25%以上つややかになる場合にのみ、新しいシャンプーの製造に価値があると言うかもしれません。
基本的な生物学的研究を行っていると、どの程度の違いを求めているのかわからないことが多く、できる限り大きなサンプルサイズを使用したり、その分野の他の研究と同様のサンプルサイズを使用したりしたくなることがあります。 しかし、実験を行う前に、検出できる効果の種類を知るために検出力分析を行うべきです。 例えば、ワクチン反対派の人たちは、ワクチンが自閉症の原因になっているかどうかを調べるために、アメリカ政府がワクチンを接種していない子供とワクチンを接種した子供を対象とした大規模な研究を行うことを提案しています。 どのような効果の大きさが興味深いのかは明らかではありません。 あるグループの自閉症が10%多いか? あるグループの自閉症が10%多いのか、50%多いのか、2倍多いのか。 しかし、検出力分析によると、米国内の3歳から6歳までのワクチンを接種していない子どもと、同数のワクチンを接種した子どもを対象とした研究であっても、有意な差が出る可能性を高くするためには、一方のグループで自閉症が25%多く発生しなければなりません。 ワクチンを接種していない子どもたち5,000人とワクチンを接種した子どもたち5,000人を対象とした、より現実的な研究では、一方のグループで自閉症が他方のグループよりも3倍多い場合にのみ、高い検出力で有意な差を検出することができます。 ワクチン接種を受けた子供と受けていない子供の間で自閉症にそれほど大きな差があるとは考えにくいため、また、そのような研究で関係を見つけられなかったとしても、ワクチン接種反対派の人たちが関係がないと納得することはないため (関係がないと納得するものは何もない。それが彼らを変人にしているのだ)、検出力分析は、そのような大規模で高価な研究が価値のないものであることを示しています。 分析を行う前に、それぞれの値を選択する必要があります。
効果量
効果量は、検出したい帰無仮説からの最小偏差です。 たとえば、鶏に何かを投与することで、雛の性比が変化することを期待している場合、求めている性比の変化の最小値は 10% であると決定することができます。 その場合、効果量は10%となります。 鶏がより多くの卵を産むようにするためのテストであれば、効果の大きさは月に2個の卵かもしれません。
時には、特定の効果量を選択するための経済的または臨床的な理由があるでしょう。 月々1.5ドルの鶏の餌のサプリメントをテストする場合、毎月1.5ドル分以上の余分な卵を産むかどうかを知りたいだけです。 しかし、生物学の基本的な研究では、効果の大きさは、自分で考えた丸い数字に過ぎません。 例えば、プロモーター領域の突然変異が遺伝子発現に影響を与えるかどうかを調べるために、検出力分析を行うとします。 遺伝子発現の変化はどのくらいの大きさを求めていますか? 10%? 20%? 50%? かなり恣意的な数字ですが、あなたの科学のために高価な小さな命を捧げてくれるトランスジェニックマウスの数に大きな影響を与えます。 特定の効果量を求める正当な理由がない場合は、そのことを認めて、X軸にサンプルサイズ、Y軸に効果量のグラフを描いたほうがいいでしょう。
α
αは検定の有意水準(P値)であり、帰無仮説が真であっても棄却される確率(偽陽性)を表します。 通常の値はα=0.05です。 累乗計算機の中には片側アルファを使うものがありますが、これは紛らわしいです。
ベータまたは検出力
検出力分析におけるベータとは、実際の差が最小の効果量に等しい場合に、帰無仮説が偽であっても (偽陰性)、それを受け入れる確率のことを言います。 検定の検出力とは、実際の差が最小の効果量に等しい場合に、帰無仮説を棄却する(有意な結果を得る)確率のことです。 検出力は1-βです。 80%の検出力(ベータ値が20%に相当)が最も一般的ですが、50%や90%を使う人もいます。 偽陰性のコストは、検出力の選択に影響します。効果量を確実に検出したいのであれば、検出力の値を大きくして(ベータ値を小さくして)、サンプルサイズを大きくします。 ベータ値の入力を求める検出力計算機もあれば、検出力 (1-ベータ値) の入力を求める計算機もありますので、どちらを使用する必要があるかをよく理解してください。
標準偏差
測定変数の場合、標準偏差の推定値も必要です。 標準偏差が大きくなると、有意な差を検出するのが難しくなるため、より大きなサンプル サイズが必要になります。 標準偏差の推定値は、パイロット実験や公開されている文献に記載されている類似の実験から得ることができます。
名目変数の場合、標準偏差はサンプル サイズの単純な関数なので、個別に推定する必要はありません。
How it works
検出力分析の詳細は、異なる統計的検定で異なりますが、基本的な概念は似ています。 手首の骨折を研究していて、帰無仮説は「片方の手首を骨折した人の半分は右手首を骨折し、半分は左手首を骨折する」というものだと想像してみてください。 右手首を骨折した人の割合が60%以上、または40%以下であれば、正確な二項検定で有意な結果を得たいと考え、最小の効果量を10%と決めました。 なぜ10%を選んだのかはわかりませんが、それを使うことになります。 アルファはいつものように5%です。 つまり、右手首の骨折の割合が実際に40%または60%である場合、90%の確率で有意な結果(P<0.05)が得られ、10%の確率で有意でない結果(この場合は偽陰性)が得られるようなサンプルサイズにします。
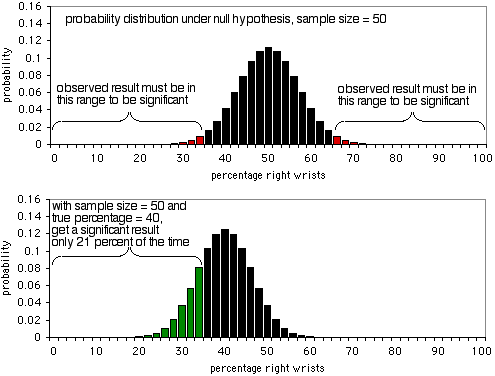

最初のグラフは、帰無仮説の下での確率分布を示しています。 サンプルサイズが50人の場合です。 帰無仮説が真であれば、右手首を骨折した人が36%未満または64%以上になる(誤検出)ことが約5%あります。 2つ目のグラフが示すように、真の割合が40%の場合、サンプルデータが36%未満または64%以上になるのは、21%の確率です。 明らかに、50 のサンプル サイズはこの実験には小さすぎます。たとえ右手首と左手首の破損の割合が 40:60 であっても、21% の確率で有意な結果が得られます。
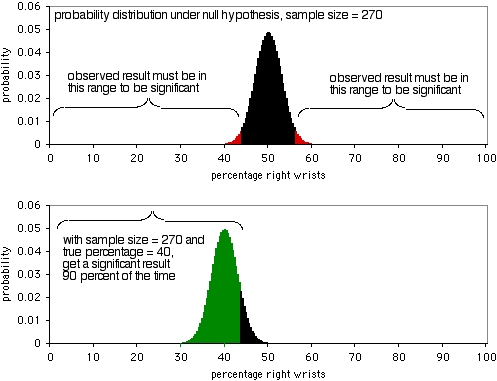

次のグラフは、帰無仮説のもとでの確率分布を示しています。 サンプルサイズが270人の場合です。 P<0.05レベルで有意であるためには、観察された結果は、右手首を骨折する人の割合が43.7%未満または56.3%以上でなければなりません。 2つ目のグラフが示すように、もし真の割合が40%であれば、サンプルデータは90%の確率でこのような極端な値になります。 この実験では、270個のサンプルサイズがかなり良いです。右手首と左手首の骨折の割合が40:60であれば、90%の確率で有意な結果が得られます。
例
あなたは、黄色が優性である黄/緑のエンドウ色のヘテロ接合体であるエンドウ豆を交配することを計画しています。 予想される子孫の比率は、黄3:緑1です。 1 緑です。 あなたは、黄色のエンドウ豆が実際に適合しているのかしていないのかを知りたいと思っています。 あなたは任意で、黄エンドウの数が予想よりも3%多いか少ないかの違いを有意(P<0.05)に検出できるサンプルサイズを、90%の検出力で決定しました。 サンプルサイズが十分小さい場合は適合度の正確な二項検定を、サンプルサイズが大きい場合は適合度のG検定を使ってデータを検定します。
適合度の正確検定で説明したように G*Power を使用すると、黄色のエンドウ豆の真の割合が 78% の場合、90% の確率で有意 (P<0.05) な結果を得たい場合は 2109 本のエンドウ豆が必要であり、真の割合が 72% の場合は 2271 本のエンドウ豆が必要であるという結果になります。 どちらかの方向への偏差に興味があるので、大きい方の数字である2271を使用します。 豆の数は多いですが、馬鹿げた数ではないことがわかって安心しました。 黄色いエンドウ豆の期待値と観測値の間に0.1%の差を検出したい場合、197万142個のエンドウ豆が必要だと計算できます。もしそれを検出する必要があるなら、サンプル サイズの分析により、エンドウ豆を選別するロボットを予算に含めなければならないことがわかります。
2 標本 t 検定のデータ例では、「生物学的データ解析」の午後 2 時の部の平均身長は 66.6 インチ、午後 5 時の部の平均身長は 64.6 インチでしたが、その差は有意ではありませんでした (P=0.207)。 このような大きな差を80%の確率で有意にするためには、何人の学生をサンプリングしなければならないかを知りたいと思います。 2標本のt-検定のページで説明されているように、G*Powerを使って、平均値の差に2.0を入力します。 ExcelのSTDEV関数を使って、元のデータの各標本の標準偏差を計算します。それは、標本1で4.8、標本2で3.6です。 アルファに0.05、検出力に0.80を入力します。 結果は72で、もし午後5時の生徒が午後2時の生徒よりも2インチ短い場合、本当の差が2.0インチであれば、80%の確率で有意差を検出するには、各クラスに72人の生徒が必要だということです。
検出力分析の方法
G*Power
G*Powerは優れた無料のプログラムで、MacとWindowsに対応しており、さまざまなテストの検出力分析を行うことができます。 このハンドブックでは、ほとんどのテストの検出力分析にG*Powerを使用する方法を説明します。
R
Salvatore Mangiafico氏のR Companionには、このハンドブックに掲載されているテストの多くについて、検出力分析を行うサンプルRプログラムがあります。 必要なパラメータ(テストによって異なります)を入力し、解こうとしているパラメータ(通常はntotal(総サンプルサイズ)またはnpergroup(各グループのサンプル数)のピリオド(SASでは欠損データを表す)を入力します。 この目的ではSASよりもG*Powerの方が使いやすいと思いますので、パワー分析にSASを使うことはお勧めしません。
⇐ 前のトピック|次のトピック ⇒ 目次
このページの最終更新日は2015年7月20日です。 そのアドレスはhttp://www.biostathandbook.com/power.htmlです。 It may be cited as:
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. このWebページには、印刷版の40~44ページの内容が含まれています。
©2014 by John H. McDonald. このコンテンツであなたが望むことはおそらくできます。詳細は許可のページをご覧ください。