Learning Objectives
このセクションの終わりには、以下のことができるようになります。
- 減衰調和運動の動きを説明する
- 減衰調和振動の運動方程式を書く
- 駆動された、または強制された、減衰調和運動の動きを説明する
- 強制された、減衰調和運動の運動方程式を書く
現実の世界では、振動が真のSHMに従うことはほとんどありません。 通常、何らかの摩擦が運動を減衰させるために作用し、その結果、振動が消滅するか、継続するためにはより大きな力が必要となります。
ギターの弦は、弾いてから数秒後には振動しなくなります。
ギターの弦は、弾くと数秒後には振動しなくなります。遊び場のブランコで揺れ続けるには、押し続けなければなりません((図))。 摩擦やその他の非保存的な力を小さくしたり無視したりすることはよくありますが、完全に減衰しない運動はまれです。

図15.24 減衰力を打ち消すためには、ブランコを押し続ける必要があります。 (credit: Bob Mical)
(図)は、質量mが力定数kのばねに取り付けられています。質量は、初期振幅{A}_{0}の位置まで持ち上げられた後、解放されます。 質量は、粘性のある流体中で平衡位置の周りを振動しますが、振幅は振動するたびに小さくなります。 ダンピング量が少ないシステムでは、周期と周波数は一定で、SHMとほぼ同じですが、振幅は図のように徐々に小さくなります。

図15.25 粘性流体中で振動するばね上の質量について、周期は一定ですが、流体による減衰のために振動の振幅は減少します。 この章の前半で説明したように、重りの唯一の寄与は平衡位置を変えることであることに注意してください。 したがって、正味の力はバネの力と減衰力({F}_{D})に等しくなります。 速度の大きさが小さい、つまり質量がゆっくりと振動する場合、減衰力は速度に比例し、運動方向に対して作用します({F}_{D}=text{-}bv)。 したがって、質量にかかる正味の力は
これをxの微分方程式として書くと
この方程式の解を求めるために、(図)に示す位置と時間のプロットを考えます。 この曲線は、指数関数{A}_{0}{e}^{text{-}\pha t}の包絡線の中で振動する余弦曲線に似ています(ここで\pha =frac{b}{2m})。 この解は
これが実際に解であることを証明するための練習として残されています。 正しい解であることを証明するために、時間に対する1次および2次導関数を取り、(図)に代入します。 これにより、(Figure)が以下の場合に解となることがわかります。
SHMを受ける質量の角周波数は、力の定数の平方根を質量で割ったものに等しいことを思い出してください。 これはしばしば固有角周波数と呼ばれ、次のように表されます
減衰調和運動の角周波数は
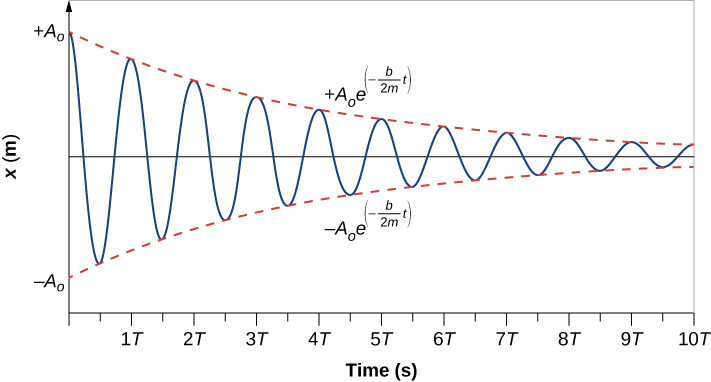
図15.26 粘性流体中のバネの上で振動する質量の位置対時間。
減衰調和運動の説明を始めたときに、減衰は小さくなければならないと述べたことを思い出してください。 2 つの質問が思い浮かびます。 なぜダンピングは小さくなければならないのか? また、小さいとはどの程度の大きさなのか? システムの減衰量を徐々に増やしていくと、周期と周波数に影響が出始めます。これは、減衰が前後の動きに逆らって、それを遅くするためです。 ダンピングが非常に大きい場合、システムは振動すらせず、ゆっくりと平衡状態に向かっていきます。 角周波数は次のようになります。
bが大きくなると、\frac{k}{m}-{(\frac{b}{2m})}^{2}は小さくなり、最終的にはb=sqrt{4mk}のときに0になります。
(図)はダンピング量を変えたときの調和振動子の変位を示しています。
(図)はダンピング量を変えたときの調和振動子の変位を示しています。ダンピング定数が小さいとき、b<sqrt{4mk}。 とすると、運動の振幅は指数関数的に減衰しながら振動します。 この系は、曲線(a)のように、アンダーダンピングされていると言われます。 多くの系はアンダーダンピングであり、ばねの上で振動する質量のように、振幅が指数関数的に減少しながら振動します。 減衰は非常に小さいかもしれませんが、最終的には質量は静止します。 減衰定数がb=Sqrt{4mk}であれば、システムは臨界状態にあると言えます。 となると、曲線(b)のように、システムは臨界的に減衰していると言えます。 臨界減衰系の例としては、自動車のショックアブソーバーなどが挙げられます。 振動ができるだけ早く減衰するのが有利です。 ここでは、システムは振動せずに、できるだけ早く平衡状態に漸近します。 (図)の曲線(c)は、b>sqrt{4mk}がオーバーダンピングされた系です。

図15.27 粘性流体中の質量とバネからなる3つの系の位置と時間の関係。 (a) 減衰が小さい場合 (b<sqrt{4mk}) は、質量は振動し、エネルギーが非保存的な力によって散逸するにつれて、ゆっくりと振幅を失います。 リミットケースは(b)で、ダンピングが(b=sqrt{4mk})の場合です。
このようなシステムは急速に平衡状態に戻り、また平衡状態を維持するため、臨界ダンピングがしばしば望まれます。 さらに、臨界ダンピングされたシステムに一定の力を加えると、システムは新しい平衡位置に最短時間で移動し、新しい位置でオーバーシュートしたり振動したりすることはありません。
理解度チェック
なぜ完全に減衰しない調和振動子はそれほど珍しいのでしょうか?
概要
- 減衰した調和振動子には、エネルギーを散逸させる非保存的な力があります。
- 臨界減衰は、オーバーシュートすることなく、できるだけ早くシステムを平衡に戻します。
- 減衰不足のシステムは、平衡位置を通って振動します。
- 減衰過剰のシステムは、臨界的に減衰されたシステムよりも、よりゆっくりと平衡に向かって動きます。
Conceptual Questions
減衰調和振動子の例を挙げてください。
それぞれの条件で、車がぶつかった後、どのように跳ねるか。
(a)オーバーダンピング
(b)アンダーダンピング
(c)臨界ダンピング
ほとんどの調和振動子はダンピングされており、無駆動の場合、最終的には停止します。 なぜでしょうか
問題
軽く減衰した振動子の振幅は、1サイクルの間に3.0%減少します。 各サイクルで失われる振動子の機械的エネルギーの割合は?
用語解説
批判的に減衰された状態で、振動子の減衰により、振動せずに平衡位置にできるだけ早く戻ること。 臨界減衰状態とは,振動子の減衰により,振動せずに平衡状態にできるだけ早く戻る状態をいう。 SHMで振動するシステムの自然角周波数 SHMで振動するシステムの自然角周波数 オーバーダンピング状態とは,振動子の減衰により,振動せずに平衡状態にできるだけ早く戻る状態をいう。 振動子が平衡に向かって、臨界減衰系よりもゆっくりと移動する状態 振動子の減衰により、減衰した調和振動子の振動の振幅が時間とともに減少し、最終的にゼロに近づく状態
div