![]()
![]()

二項分布は、離散的な確率分布
を与えます。 二項分布は、![]()
![]()
![]()
![]()
![]() で偽となる場合)p)となります。) したがって、二項分布は次のように与えられます
で偽となる場合)p)となります。) したがって、二項分布は次のように与えられます
|
(1)
|
|||
|
(2)
|
ここで![]()
![]()
![]()
![]() 回の成功の分布を示しています。
回の成功の分布を示しています。
二項分布はWolfram LanguageではBinomialDistributionとして実装されています。
二項分布で観測される![]() より多くの成功を得る確率は
より多くの成功を得る確率は
where
![]()
![]() は不完全ベータ関数です。
は不完全ベータ関数です。
二項分布の特性関数は
|
(5)
|
(Papoulis 1984, p. 154). 瞬間的な分布のモーメント生成関数![]() は
は
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
平均値は
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
0に関するモーメントは
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
従って、平均に関するモーメントは
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
スキューネスとクルトシスエクスセスは
|
(22)
|
|||
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
最初のキュムラントは
|
(26)
|
そしてそれに続くキュムラントは recurrencerelation
|
(27)
|
平均偏差は次のように与えられます。 平均偏差は次のように与えられます
|
(28)
|
特別な場合![]() については、次のようになります。 これは次のようになります
については、次のようになります。 これは次のようになります
|
(29)
|
|||
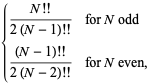 |
(30)
|
ここで、![]()
![]() , 2, …の場合、最初のいくつかの値は、したがって、1/2, 1/2, 3/4, 3/4, 15/16, 15/16, …となります。 となります(OEIS A086116およびA086117)。 一般的なケースは次のように与えられます
, 2, …の場合、最初のいくつかの値は、したがって、1/2, 1/2, 3/4, 3/4, 15/16, 15/16, …となります。 となります(OEIS A086116およびA086117)。 一般的なケースは次のように与えられます
|
(31)
|
Steinhaus(1999, pp. 25-28)は、大きさ![]()
![]()
![]()
![]() を無作為に分配した後に考察しています。
を無作為に分配した後に考察しています。
|
(32)
|
![]() とすると、以下の表にまとめた結果が得られます。
とすると、以下の表にまとめた結果が得られます。
| 0 | 23.3591 |
| 1 | 23.7299 |
| 2 | 11.8650 |
| 3 | 3.89221 |
| 3 | 3.89221 |
| 4 | 0.942162 |
| 5 | 0.942162 |
| 5 | 0.179459 |
| 6 | 0.0280109 |
| 7 | 0.0036840 |
| 8 | |
| 9 | |
| 9 | |
| 10 | |
大きな![]()
![]() について展開することで得ることができます。 i.e.,
について展開することで得ることができます。 i.e., ![]()
![]() とすると、
とすると、
|
(33)
|
where
|
(34)
|
しかし、私たちは最大値について展開しています。
|
(35)
|
これは、![]()
![]() と書けます。 さて、(◇)の対数をとると
と書けます。 さて、(◇)の対数をとると
大きな![]()
![]() ではスターリングの近似を用いることができる
ではスターリングの近似を用いることができる
|
(37)
|
ソ
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
|||
|
(41)
|
|||
|
(42)
|
and
|
(43)
|
![]()
![]() nを解きます。
nを解きます。
|
(44)
|
|
(45)
|
|
(47)
|
![]() なので。 これで、拡張の項を見つけることができます
なので。 これで、拡張の項を見つけることができます
|
(48)
|
|||
|
(49)
|
|||
|
(50)
|
|||
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
|||
|
(55)
|
|||
|
(56)
|
|||
|
(57)
|
|||
|
(58)
|
|||
|
(59)
|
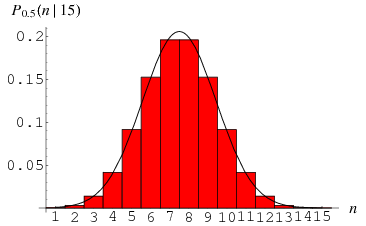
さて、分布を連続的なものとして扱います。
各項は前の項より小さいオーダー![]()
![]() 以上の項は無視できます。
以上の項は無視できます。
|
(61)
|
確率を正規化する必要があります。 そこで
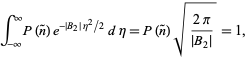 |
and
|
(63)
|
|||
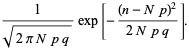 |
(64)
|
![]() を定義します。
を定義します。
|
(65)
|
これは、正規分布です。 したがって、二項分布は、![]()
![]()
![]() が小さくても)正規分布で近似されます。
が小さくても)正規分布で近似されます。
![]()
![]()
![]()
![]() を持つポアソン分布に収束します。
を持つポアソン分布に収束します。
![]()
![]()
![]()
![]()
![]()
![]() の条件付き確率は
の条件付き確率は
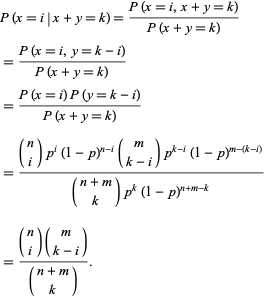 |
これが超幾何学的分布であることに注意してください
。