Heading

Interquartile Rangeとは

Interquartile Rangeとは、データセットの中で「中間の50％」がどこにあるかを示す尺度です。 範囲がデータセットの最初と最後の位置を示す指標であるのに対し、四分位範囲は値の大部分がどこにあるかを示す指標です。

四分位間範囲の公式は、第 1 四分位から第 3 四分位を引いたものです：

Contents (click to skip to the page section):

手で解く:

1. 手で式を解く（奇数の集合）
2. 偶数の集合の場合はどうするか
3. 奇数の集合の四分位範囲を求める。 第二の方法
4. 箱ひげ図の四分位範囲。 求め方

テクノロジーを利用する。

1. Minitabでの四分位範囲
2. Excelでの四分位範囲
3. SPSSでの四分位範囲
4. TI83での四分位範囲
5. TI89でのQ1、Q3とIQR

一般的な情報です。

1. 四分位範囲とは何ですか?
2. 四分位範囲の公式とは
3. 正規分布のテストとしてのIQR
4. 四分位範囲は何に使われるのか
5. 四分位範囲の歴史

手書きで公式を解く

以下のビデオを見るか、手順を読んでみてください。 それでも問題が解決しない場合は、Chegg.comのチューターをご利用ください。

Steps:

• Step 1: 数字を順番に並べます。
  1、2、5、6、7、9、12、15、18、19、27.
• Step 2: 中央値を求めます。
  1、2、5、6、7、9、12、15、18、19、27.
• Step 3: 中央値より上と下の数字を括弧で囲います。
  統計的には必要ありませんが、Q1とQ3を見つけやすくします。
  （1、2、5、6、7）、9、（12、15、18、19、27）。
• Step 4: Find Q1 and Q3
  Q1をデータの下半分の中央値と考え、Q3をデータの上半分の中央値と考えます。
  (1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27)。 Q1＝5、Q3＝18となります。
• ステップ5：Q3からQ1を引いて四分位範囲を求めます。
  18 – 5 = 13となります。

解説が気に入った方は、ぜひご覧ください。

What if I Have an Even Set of Numbers?

例題です。 以下のデータセットのIQRを求めてください。

• Step 1: 数字を順番に並べる：
  3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
• Step 2: データの中心に印をつける：
  3, 5, 7, 8, 9, | 11, 15, 16, 20, 21.
• ステップ3：ステップ2で作ったマークの上下にある数字を括弧で囲むと、Q1とQ3がわかりやすくなります。
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).
• Step 4: Q1とQ3を求める
  Q1はデータの下半分の中央値（真ん中）、Q3はデータの上半分の中央値（真ん中）です。
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7、Q3 = 16です。
• Step 5: Q3からQ1を引きます。
  16 – 7 = 9です。
  これがIQRです。

Back to Top

奇数の集合に対する四分位範囲を見つける。 別の方法

すでにご存知かもしれませんが、統計学には「決まったもの」はありません。ある統計学者は、奇数の集合に対する四分位範囲を求めるとき、両四分位に中央値を含めます。 例えば、次のような数字の集合では
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
これで偶数の集合が2つになりますので、上記の手順でIQRを求めることができます。
トップへ戻る

Box Plotの四分位範囲。

ビデオを見るか、以下の手順をお読みください：

Box Plot interquartile range: 求め方

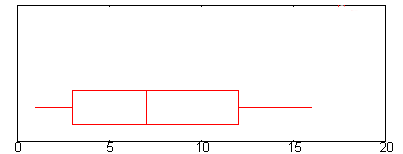
例題です。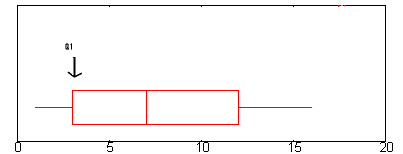

上のグラフでは、Q1はおよそ2.6の位置にあります。

Step 2: Find Q3.
Q3はボックスプロット上では「ボックス」の右端で表されます。

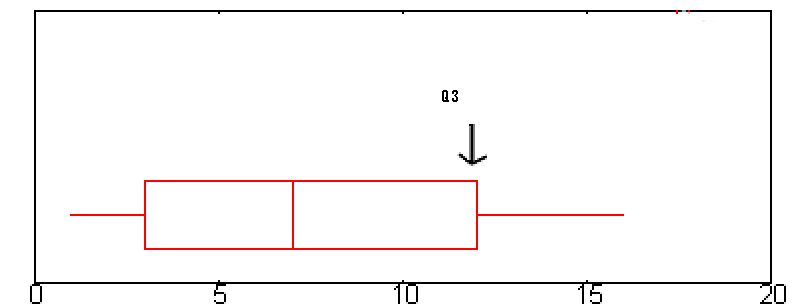
Q3はこのグラフでは約12です。

以上です！

トップへ戻る

Interquartile Range in Minitab

ステップバイステップの説明を読むか、以下のビデオバージョンをご覧ください。

Interquartile Range in Minitab: 手順

例題です。 次のデータセットのグレードポイント平均（GPA）について、Minitabで四分位範囲を求めます：
グレードポイント平均（GPA）：1（3.2）、1（3.1）、2（3.5）、2（2.0）、3（1.9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5(3.3), 6(3.4), 6(2.6), 6(2.5), 7(2.0), 7(1.5), 8(4.0), 8(2.0).

ステップ1: Minitabのワークシートにデータを入力します。 1列または2列にデータを入力します。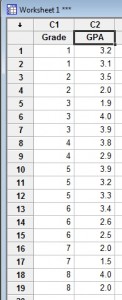

ステップ2：「統計」→「基本統計」→「記述統計の表示」をクリックして、記述統計メニューを開きます。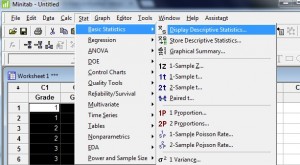

Step 3: 左側のウィンドウで変数名をクリックし、「選択」ボタンをクリックして右側のウィンドウに変数名を移します。

ステップ4：「統計」ボタンをクリックします。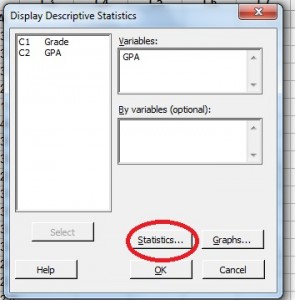

ステップ5：「四分位範囲」にチェックを入れます。”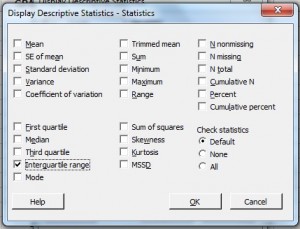
.

Step 6: “OK “ボタンをクリックします（新しいウィンドウが開いて結果が表示されます）。 このデータセットのGPAのIQRは1.8です。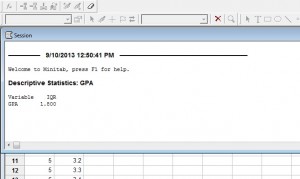

以上です。

ヒント: 記述的な統計情報がウィンドウに表示されない場合は、ツールバーの “Window” をクリックし、次に “Tile” をクリックします。

トップへ戻る

四分位範囲の求め方 Excel 2007

Excel 2007で四分位範囲を求めるには、ビデオを見るか、以下の手順を読んでください:

手順：
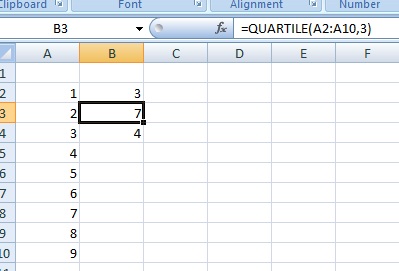
ステップ1：データをワークシート上のExcelの1つの列に入力します。 例えば、セルA2からA10にデータを入力します。

Step 2: 空白のセルをクリックして（例えば、セルB2をクリック）、「=QUARTILE(A2:A10,1)」と入力します。 A2:A10は、データセットの実際の値に置き換える必要があります。 たとえば、データをB2からB50に入力した場合、式は=QUARTILE(B2:B50,1)となります。 このExcelの数式(A2:A10,1)の「1」は、第1四分位（つまり、データセットの25％の位置にある点）を表しています。

ステップ3：2つ目の空白セルをクリックし（たとえば、セルB3をクリック）、「=QUARTILE(A2:A10,3)」と入力します。 A2:A10をデータセットの実際の値に置き換えます。 このExcelの数式(A2:A10,3)の「3」は、第3四分位値(すなわち、データセットの75%に位置する点)を表しています。

ステップ4：3番目の空白セル(たとえば、セルB4をクリック)をクリックし、「=B3-B2」と入力します。 ステップ2と3の四分位関数が異なる場所にある場合は、セルの参照を変更します。

ステップ5：「Enter」キーを押します。 Excelは、ステップ4でクリックしたセルにIQRを返します

以上です！

トップへ戻る

SPSSで四分位範囲を求める方法

多くの技術と同様に、SPSSにもIQRを計算する方法がいくつかあります。 しかし、最も直感的に見つけられる方法（「記述統計 > 頻度」）をクリックすると、驚くべきことに、IQRはリストアップされません（ただし、第1、第2、第3四分位値はリストアップされます）。 この方法では、第1四分位から第3四分位を引いてIQRを求めることができます。 しかし、SPSSで四分位範囲を求める最も簡単な方法は、”Explore “コマンドを使うことです。

ビデオを見るか、以下の手順をお読みください：

Steps

Step 1: SPSSで新しいデータファイルを開きます。 ファイル」をクリックし、「新規」にマウスオーバーして「データ」をクリックします。

Step 2: データをワークシートの列に入力します。 列数は必要に応じていくつでも使用できますが、空白の行やデータ間のスペースを残さないようにしてください。 ご覧ください。

Step 3: “Analyze “をクリックして、”Descriptive Statistics “にマウスオーバーします。

Step 4: 変数名(これは列の見出しの格好の名前です)をクリックし、上矢印をクリックして、変数を「従属リスト」ボックスに移動します。

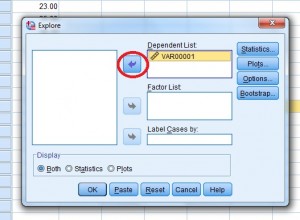
The “Explore” variables dialog box.

Step 5: “OK “をクリックします。 四分位範囲が「Descriptives」ボックスに表示されます。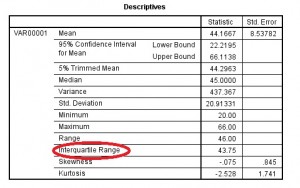

ヒント：この例では、データシートに入力されたリストは1つだけですが、データの入力方法によっては、複数のリストを選択できる場合があります。 先に進む前に、正しい変数 (列名) を選択していることを確認してください。 より印象的な変数名にしたい場合は、ワークシートの一番左下にある「変数表示」ボタンをクリックして、列のタイトルを変更します。
Back to Top

Interquartile Rangeとは

セット内のすべてのデータを数直線上の点として想像してください。 例えば、3、7、28のデータがある場合、それらは0を中心に、0より無限に下と0より無限に上に伸びる数直線上の点だと想像してください。 数直線上にプロットすると、データセットの最小のデータポイントと最大のデータポイントが、データセットのすべてのデータポイントを含む数直線上の空間の区間の境界（つまり、下限と上限）を作ります。

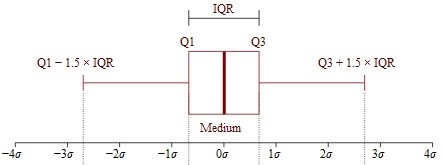
四分位範囲とは、データセットの真ん中の50％の長さのことです。 Box and whiskers image by Jhguch at en.wikipedia

IQRを正式な言葉で知りたい場合、IQRは次のように計算されます。

IQRは、正式には次のように計算されます。 四分位数とは、データの集合を4等分する方法を示す言葉です（quarterと考えてください）。

IQRの例

データポイント1、3、5、7、8、10、11、13を含むセットがある場合、第1四分位値は4、第2四分位値は7.5、第3四分位値は10.5となります。 これらの点を数直線上に描くと、これらの3つの数字が数直線を1から13までの4分の1に分けていることがわかります。 したがって、このデータセットのIQRは、10.5から4を引いた6.5となります。 第1四分位値と第3四分位値は、25%と75%と呼ばれることもありますが、これは、データセットを4分の1ではなく、パーセントで分割した場合に相当する数値だからです。

トップへ戻る

TI83を使用した四分位範囲

ビデオを見るか、以下の手順を読んでください:

このウェブサイトにある便利なオンライン四分位範囲計算機を使用することができますが、小テストやテストではその選択肢がないかもしれません。 ほとんどの教官は、テストでのTI-83の使用を許可しており、AP統計学の試験でも許可されている数少ない電卓の1つです。

例題: 世界のトップ 10 ビル (2009 年現在) の高さについて、TI 83 の四分位範囲を求めます。 高さ（単位：フィート）は

Steps

Step 1: 上記のデータを TI 83 電卓のリストに入力します。 STATボタンを押して、ENTERを押します。 最初の数字（2717）を入力し、ENTERを押します。

Step 2：STATボタンを押します。

Step 3：右矢印ボタン（矢印キーはキーパッドの右上にあります）を押して、”Calc. “を選択します。”

Step 4：ENTERを押して、”1-Var Stats “をハイライトします。

Step 5：もう一度ENTERを押して、Statsのリストを表示します。

Step 6：矢印キーでリストをスクロールして、Q1とQ3を見つけます。 その数字を書き留めます。

1. 矢印キーを使用して、ハイライトしたい
   テキストの先頭にカーソルを置きます。
2. TI キーボードを使用して、Shift キーを押したまま、矢印キーを使用してテキストをハイライトします。

コピー＆ペーストのメニューが表示され、データをコピー＆ペーストすることができます。

Step 7:Q3からQ1を引いてIQRを求める（strong>この数字では624フィート）

以上で完了です。
トップへ戻る

Q1、Q3、四分位範囲TI 89の求め方

ビデオを見るか、以下の手順を読んでください:

例題: 次の数字のリストについて、Q1、Q3、IQRを求めます。 1, 9, 2, 3, 7, 8, 9, 2.

Step 1: APPSを押します。 Stats/List Editor」にスクロールします（スクロールにはキーパッドの矢印キーを使用します）。 ENTERを押します。

Step 2: リストエディターのデータを消去：F1 8を押します。

Step 3: ALPHA 9 ALPHA 1 ENTERを押します。

Step 4: 数字を1つずつ入力していきます。 それぞれの入力の後に、ENTERキーを押します。

Step 5: F4を押し、ENTERを押します（1-var stats画面）。

Step 6: 電卓に「IQ」と呼ばれるリストの統計を取りたいことを、「List: 」ボックスにALPHA 9 ALPHA 1と入力して伝えます。 電卓は自動的にカーソルをそこに置いてくれるはずです。

Step 7:結果を読んでみましょう。 Q1はQ1Xと表示されます（この例ではQ1X=2）。 Q3はQ3Xと表示されています（Q3X=8.5）。 IQRを求めるには、ホーム画面でQ3からQ1を引きます。

以上です！

トップへ戻る

四分位範囲の計算式とは

IQRの計算式は次のとおりです：
IQR = Q3 – Q1

ここでQ3は上位四分位、Q1は下位四分位です。

IQR as a test for normal distribution

母集団が正規分布を持っているかどうかをテストするために、平均値と標準偏差を用いてinterquartile range formulaを使用します。 母集団が正規分布しているかどうかを判断する式は以下の通りです：
Q1 – (σ z1) + X
Q3 – (σ z3) + X
ここで、Q1は第1四分位、Q3は第3四分位、σは標準偏差、zは標準スコア（「zスコア」）、Xは平均値です。 母集団が正規分布しているかどうかを判断するには、両方の式を解き、結果を比較します。 もし、結果と第1四分位または第3四分位との間に有意な差があれば、その母集団は正規分布していません。

トップへ戻る

Interquartile Rangeは何に使われるのか

IQRは、あるデータセットのデータポイントがデータセットの平均からどれだけ広がっているかを測定するために使われます。 IQRが大きければ大きいほど、データポイントが広がっていることになり、逆にIQRが小さければ小さいほど、データポイントが平均の周りに集まっていることになります。 IQRの範囲は、データセット内のデータポイントがどれだけ広がっているかを測定するために使用される多くの測定方法の1つです。
Back to Top

Where Does the term Interquartile Range comes from?

“Interquartile Range “という言葉は誰が作ったのでしょうか?

歴史

イギリスの医師、Sir Donald MacAlisterは、1879年に出版された『the Law of the Geometric Mean』の中で、lower quartileとhigher quartileという言葉を使っていました。 Proc. R. Soc. XXIX, p. 374: “

医師でありながら数学の才能に恵まれ、1877年にはケンブリッジ大学の数学の最終試験で最高点を獲得しました。

マカリスターの論文「幾何平均の法則」は、実はフランシス・ギャルトン（ギャルトン板の発明者）の質問に答えたものでした。 しかし、1882年になって、ギャルトン（「人体測定委員会の報告」）は、上四分位値と下四分位値を使い、確率誤差の2倍と定義した「四分位範囲」という言葉を使いました。 ギャルトンは単なる統計学者ではなく、人類学者、地理学者、原始人、心理測定学者でもあり、340冊以上の著書を残している。

Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, pp.20-21, 1993.

——————————————————————————

宿題やテストの問題で助けが必要ですか？ Chegg Studyでは、その分野の専門家からステップバイステップで質問に対する解決策を得ることができます。 Cheggチューターとの最初の30分は無料です。