レッスンインデックスに戻る|レッスンを順番にこなす|印刷用ページ
階乗
階乗はとてもシンプルなものです。 それはただの積で、感嘆符で示されています。 例えば、「4階乗」は「4!」と書き、1×2×3×4=24を意味します。 一般に、n! は、1からnまでのすべての整数の積を意味し、n!=1×2×3×…×nとなります。 これはもう覚えてください。 0!=1です)
- 6!を評価します。
1×2×3×4×5×6 = 720
多くの(ほとんどの?)電卓が階乗の評価をしてくれます。
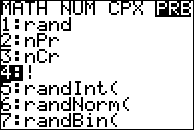

「!」ボタンの有無を確認するか、または取扱説明書を確認してください。 “ボタンを探すか、取扱説明書を確認してください。
- 12を単純化する! Copyright © Elizabeth Stapel 2004-2011 All Rights Reserved
12! = 1×2×3×4×… ああ、これはもうだめだ。

12! = 479001600
Advertisement
組み合わせや順列、確率などを行うようになると、分子や分母に階乗がある式を簡略化することになります。 例えば、
- 次のように簡略化します。
![]()
電卓でこんなことができます:

階乗の定義から計算することもできます:
![]()
どちらの場合も、6! ÷ 4! = 30
前の問題で、たくさんの数字を打ち消すことができたことに注目してください。
- 次のように簡略化されます。
![]()
すぐに、17!と14!の両方に共通する1から14までの因子をキャンセルすることができます。
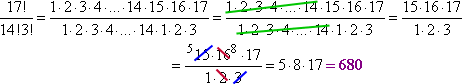
途中でギャップ (エリプシス、またはトリプル ピリオド) を残すことで、書かなければならないことを短くしたことに注目してください。 このギャップとキャンセルのプロセスは、後で便利になるでしょう (微積分のように、このテクニックをたくさん使うことになるでしょう)。 例えば、
- 次のように簡略化されます:
![]()
数字ではなく変数を扱っているので、私の電卓ではこれを評価できません。 手作業でこれを単純化する必要があります。 これを行うために、私は、相殺できるものを持つために十分な数の因子を使用して、階乗を書き出します。 数」の問題に戻って考えてみると、連続した整数は 1 単位ずつ離れているので、積 (n + 2) の因子は次のような形になります。×(n – 1)×(n)×(n + 1)×(n + 2)
因子のリストを「n – 1」まで遡ることで、相殺できる因子のリストを作成しました:
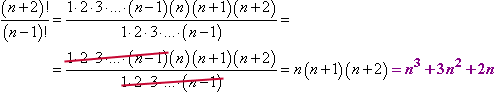
そのキャンセルを処理する方法に注目してください。 私は、重複する因子をキャンセルできる場所がわかるように、階乗式を十分に拡張しました。 nが何であるかわからなくても、キャンセルすることができました。
階乗の最後にあるゼロの数を見つける方法については (「23 の最後にはゼロがいくつあるか? after you multiply it out」のように)、このノートを見てください。
Top|Return to Index
|
Cite this article as: |
Stapel, Elizabeth. “Factorials.” Purplemath. Available from 2016
|