Następny: 8.5 Cykle energetyczne Rankine’a Up: 8. Cykle energetyczne z Previous: 8.3 Cykl Carnota Spis treści
Do tej pory rozważaliśmy tylko gazy idealne i chcielibyśmy pokazać, że właściwości ![]()
![]()
![]() , itd. są prawdziwymi zmiennymi stanu i że 1. i 2. prawo termodynamiki obowiązuje, gdy medium robocze nie jest gazem idealnym (tj. medium dwufazowym). Eleganckim sposobem na zrobienie tego jest rozważenie cyklu Carnota dla medium dwufazowego. Stwierdzenie faktu, że wszystkie silniki Carnota pracujące pomiędzy dwiema danymi temperaturami mają taką samą sprawność, jest jednym ze sposobów stwierdzenia 2. prawa termodynamiki. Ciecz robocza nie musi być gazem idealnym i może być czynnikiem dwufazowym zmieniającym fazy.
, itd. są prawdziwymi zmiennymi stanu i że 1. i 2. prawo termodynamiki obowiązuje, gdy medium robocze nie jest gazem idealnym (tj. medium dwufazowym). Eleganckim sposobem na zrobienie tego jest rozważenie cyklu Carnota dla medium dwufazowego. Stwierdzenie faktu, że wszystkie silniki Carnota pracujące pomiędzy dwiema danymi temperaturami mają taką samą sprawność, jest jednym ze sposobów stwierdzenia 2. prawa termodynamiki. Ciecz robocza nie musi być gazem idealnym i może być czynnikiem dwufazowym zmieniającym fazy.
Pomysł polega na tym, aby uruchomić silnik Carnota pomiędzy temperaturami ![]() i
i![]() dla czynnika dwufazowego i pozwolić mu przejść zmianę fazy. Możemy wtedy wyprowadzić ważną zależność znaną jako równanie Clausiusa-Clapeyrona, które daje nachylenie krzywej ciśnienia pary. Następnie możemy zmierzyć krzywą prężności pary dla różnych substancji i porównać zmierzone nachylenie z równaniem Clausiusa-Clapeyrona. Można to potraktować jako eksperymentalny dowód ogólnej ważności pierwszego i drugiego prawa termodynamiki!
dla czynnika dwufazowego i pozwolić mu przejść zmianę fazy. Możemy wtedy wyprowadzić ważną zależność znaną jako równanie Clausiusa-Clapeyrona, które daje nachylenie krzywej ciśnienia pary. Następnie możemy zmierzyć krzywą prężności pary dla różnych substancji i porównać zmierzone nachylenie z równaniem Clausiusa-Clapeyrona. Można to potraktować jako eksperymentalny dowód ogólnej ważności pierwszego i drugiego prawa termodynamiki!
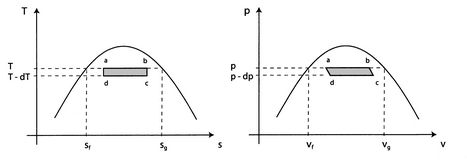
Rozważmy nieskończenie mały cykl Carnota ![]() przedstawiony na Rysunku 8.8. Ciepło jest absorbowane pomiędzy stanami
przedstawiony na Rysunku 8.8. Ciepło jest absorbowane pomiędzy stanami![]() i
i ![]() . Aby odparować arbitralną ilość masy,
. Aby odparować arbitralną ilość masy, ![]() , potrzebna jest ilość ciepła
, potrzebna jest ilość ciepła
| (8..1) |
muszą być dostarczone do systemu. Na podstawie 1. i 2. prawa termodynamiki sprawność cieplną dla cyklu Carnota można zapisać jako
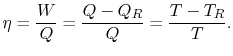 |
Stąd, dla rozważanego powyżej cyklu nieskończonego,
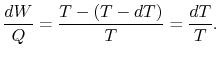 |
(8..2) |
Prace wzdłuż ![]() i
i ![]() prawie znoszą się tak, że praca netto jest różnicą pomiędzy pracą wzdłuż
prawie znoszą się tak, że praca netto jest różnicą pomiędzy pracą wzdłuż ![]() i
i ![]() , a
, a ![]() może być postrzegana jako obszar zamknięty prostokątem
może być postrzegana jako obszar zamknięty prostokątem ![]() :
:
| (8..3) |
Substituting Equations (8.1) i(8.3) do (8.2) oneobtains
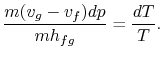 |
Porządkując wyrazy otrzymujemy równanie Clausiusa-Clapeyron equation,które definiuje nachylenie krzywej ciśnienia pary:
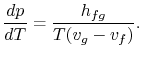 |
(8..4) |
Piękno polega na tym, że znaleźliśmy ogólny związek między doświadczalnie mierzalnymi wielkościami z pierwszych zasad (1. i 2. prawo termodynamiki).
Aby wykreślić zależność Clausiusa-Clapeyrona i porównać ją z doświadczalnie zmierzonymi krzywymi ciśnienia pary, musimy zintegrować równanie (8.4). Aby to zrobić, ciepło parowania i objętości właściwe muszą być znanymi funkcjami temperatury. Jest to ważny problem w chemii fizycznej, ale nie będziemy się nim tutaj dalej zajmować, poza wspomnieniem, że jeśli
- zmienne ciepło parowania można zaniedbać,
- założono, że faza parowa jest gazem idealnym, i
- objętość właściwa cieczy jest mała w porównaniu z objętością fazy parowej,
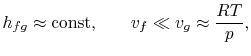 |
Integracja może być łatwo przeprowadzona8.1. Dokonując tych przybliżeń, nierówność Clausiusa-Clapeyronequation staje się
 |
Przeprowadzając całkowanie, otrzymane wyrażenie jest następujące
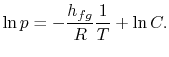 |
Należy zauważyć, że że krzywe prężności pary są liniami prostymi, jeżeli ![]() jest przedstawiony na wykresie w stosunku do
jest przedstawiony na wykresie w stosunku do ![]() i że nachylenie krzywych jest
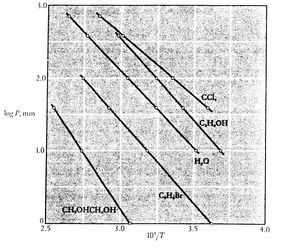
i że nachylenie krzywych jest![]() , bezpośrednio związane z ciepłem parowania.Rysunki 8.9, 8.9, i 8.22 przedstawiają krzywe ciśnienia pary dla różnych substancji. Fakt, że wszystkie znane substancje w obszarze dwufazowym spełniają równanie Clausiusa-Clapeyrona, świadczy o ogólnej ważności 1. i 2. prawa termodynamiki!
, bezpośrednio związane z ciepłem parowania.Rysunki 8.9, 8.9, i 8.22 przedstawiają krzywe ciśnienia pary dla różnych substancji. Fakt, że wszystkie znane substancje w obszarze dwufazowym spełniają równanie Clausiusa-Clapeyrona, świadczy o ogólnej ważności 1. i 2. prawa termodynamiki!

Następny: 8.5 Cykle energetyczne Rankine’a Up: 8. Cykle energetyczne z Previous: 8.3 Cykl Carnota Spis treści
UnifiedTP