Heading

Factorials to bardzo proste rzeczy. Są to po prostu iloczyny, oznaczone wykrzyknikiem. Na przykład, „czynnik czwarty” jest zapisywany jako „4!” i oznacza 1×2×3×4 = 24. W ogólności, n! („enn factorial”) oznacza iloczyn wszystkich liczb całkowitych od 1 do n; to znaczy, n! = 1×2×3×…×n.

(Z różnych powodów, 0! jest zdefiniowane jako równe 1, a nie 0. Zapamiętaj to teraz: 0! = 1.)

• Oszacuj 6!

1×2×3×4×5×6 = 720

Wiele (większość?) kalkulatorów może obliczyć czynnik za Ciebie. Na przykład, komenda factorial jest dostępna w menu „prawdopodobieństwo” na jednym z moich kalkulatorów:

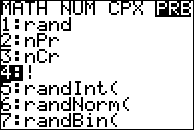
Poszukaj przycisku ” ! „, lub sprawdź instrukcję obsługi.

• Uprość 12! Copyright © Elizabeth Stapel 2004-2011 All Rights Reserved

12! = 1×2×3×4×… Och, do diabła z tym. Where’s my calculator…?



12! = 479001600

Kiedy zaczniesz robić kombinacje, permutacje i prawdopodobieństwo, będziesz upraszczał wyrażenia, które mają współczynniki w licznikach i mianownikach. Na przykład:

• Uprość następujące wyrażenia:

Mogę to zrobić w moim kalkulatorze:

Mogę też działać na podstawie definicji czynnika:



W obu przypadkach 6! ÷ 4! = 30

Zauważ, jak udało mi się anulować kilka liczb w poprzednim zadaniu. Jest to spowodowane tym, jak definiowane są współczynniki, a ta własność może bardzo uprościć twoją pracę.

• Uprość poniższe:

Od razu mogę anulować czynniki od 1 do 14, które będą wspólne zarówno dla 17! jak i 14! Następnie mogę uprościć to, co pozostało, aby otrzymać:

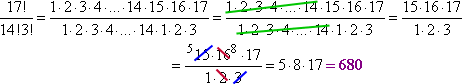
Zauważ, jak skróciłem to, co miałem do napisania, zostawiając lukę („elipsę”, czyli potrójną kropkę) w środku. Ten proces „odstępu i anulowania” przyda Ci się później (np. w rachunku, gdzie będziesz często używał tej techniki), zwłaszcza gdy masz do czynienia z wyrażeniami, z którymi Twój kalkulator sobie nie radzi. Na przykład:

• Uprość następujące wyrażenie:

Mój kalkulator nie może tego dla mnie obliczyć, ponieważ mam do czynienia ze zmiennymi, a nie z liczbami. Będę musiał uprościć to ręcznie. Aby to zrobić, wypiszę współczynniki, używając wystarczająco dużo czynników, aby mieć rzeczy, które mogą się odwołać. Myśląc z powrotem do „liczbowych” problemów słownych, kolejne liczby całkowite są oddalone od siebie o jedną jednostkę, więc czynniki w produkcie (n + 2)! mają postać:

1×2×3×4×…×(n – 1)×(n)×(n + 1)×(n + 2)

Poprzez cofnięcie się w dół listy czynników aż do „n – 1”, stworzyłem listę czynników, które mogą się anulować:

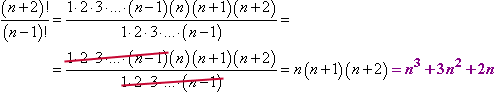
Zwróć uwagę na sposób, w jaki poradziłem sobie z tym anulowaniem. Rozszerzyłem wyrażenia czynnikowe na tyle, że mogłem zobaczyć, gdzie mogę anulować zduplikowane czynniki. Nawet jeśli nie miałem pojęcia, jakie może być n, wciąż mogłem anulować. Zapisz tę technikę w swoim mózgu, ponieważ nawet jeśli nie potrzebujesz jej teraz, prawie na pewno będziesz jej potrzebował później.

Aby uzyskać informacje na temat znajdowania liczby zer na końcu wyrażenia czynnikowego (jak „Ile zer jest na końcu 23! po pomnożeniu?”), zajrzyj do tej notatki.

Top | Return to Index

Cytuj ten artykuł jako:

Stapel, Elizabeth. „Factorials.” Purplemath. Dostępne od https://www.purplemath.com/modules/factorial.htm Stapel Elżbieta „Factorials”. Dostęp 2016