Heading

W rzeczywistym świecie oscylacje rzadko są zgodne z prawdziwym SHM. Pewnego rodzaju tarcie zazwyczaj działa tłumiąco na ruch, tak że zamiera on lub wymaga większej siły, aby go kontynuować. W tym rozdziale przeanalizujemy kilka przykładów tłumionego ruchu harmonicznego i zobaczymy, jak zmodyfikować równania ruchu, by opisać ten bardziej ogólny przypadek.

Struny gitary przestają drgać kilka sekund po ich zerwaniu. Aby nadal huśtać się na huśtawce na placu zabaw, trzeba ją pchać ((rysunek)). Mimo, że często możemy sprawić, że tarcie i inne siły niekonserwatywne są małe lub pomijalne, całkowicie nietłumiony ruch jest rzadkością. W rzeczywistości, możemy nawet chcieć tłumić oscylacje, tak jak w przypadku amortyzatorów samochodowych.

Rysunek 15.24 Aby przeciwdziałać siłom tłumiącym, trzeba ciągle pompować huśtawkę. (credit: Bob Mical)

(Rysunek) przedstawia masę m przymocowaną do sprężyny o stałej siły k. Masa jest podnoszona do położenia {A}_{0} , amplitudy początkowej, a następnie zwalniana. Masa oscyluje wokół położenia równowagi w cieczy o lepkości, ale amplituda maleje przy każdym oscylacji. Dla układu z niewielkim tłumieniem okres i częstotliwość są stałe i prawie takie same jak dla SHM, ale amplituda stopniowo maleje, jak pokazano na rysunku. Dzieje się tak, ponieważ niekonserwatywna siła tłumiąca usuwa energię z układu, zwykle w postaci energii cieplnej.

Rysunek 15.25 Dla masy na sprężynie oscylującej w lepkiej cieczy, okres pozostaje stały, ale amplitudy oscylacji maleją z powodu tłumienia spowodowanego przez ciecz.

Rozważmy siły działające na masę. Zauważmy, że jedynym wkładem masy jest zmiana położenia równowagi, co zostało omówione we wcześniejszej części rozdziału. Zatem siła netto jest równa sile sprężyny i sile tłumienia ({F}_{D}) . Jeżeli wielkość prędkości jest mała, czyli masa drga powoli, to siła tłumiąca jest proporcjonalna do prędkości i działa przeciwnie do kierunku ruchu ({F}_{D}=}bv) . Siła netto działająca na masę wynosi zatem

Pisząc to jako równanie różniczkowe w x, otrzymujemy

Aby wyznaczyć rozwiązanie tego równania, rozważmy wykres zależności położenia od czasu przedstawiony na (rys.). Krzywa przypomina krzywą kosinusową oscylującą w obwiedni funkcji wykładniczej {A}_{0}{e}^{tekst{-} t} gdzie alfa =frac{b}{2m} . Rozwiązaniem jest

Jako ćwiczenie pozostawiamy udowodnienie, że jest to, w rzeczywistości, rozwiązanie. Aby udowodnić, że jest to właściwe rozwiązanie, należy wziąć pierwszą i drugą pochodną względem czasu i podstawić je do (Rysunek). Okazuje się, że (Rysunek) jest rozwiązaniem, jeśli

Przypomnijmy, że częstotliwość kątowa masy poddawanej SHM jest równa pierwiastkowi kwadratowemu ze stałej siły podzielonej przez masę. Jest to często określane jako naturalna częstotliwość kątowa, która jest przedstawiana jako

Częstotliwość kątowa dla ruchu harmonicznego tłumionego przyjmuje postać

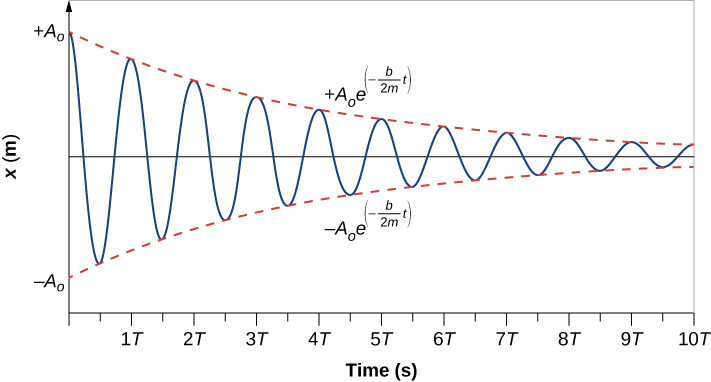
Rysunek 15.26 Położenie względem czasu dla masy oscylującej na sprężynie w lepkiej cieczy. Zauważmy, że krzywa wydaje się być funkcją cosinusową wewnątrz obwiedni wykładniczej.

Przypomnijmy, że kiedy rozpoczynaliśmy ten opis tłumionego ruchu harmonicznego, stwierdziliśmy, że tłumienie musi być małe. Nasuwają się dwa pytania. Dlaczego tłumienie musi być małe? I jak małe jest małe? Jeśli stopniowo zwiększamy ilość tłumienia w układzie, okres i częstotliwość zaczynają ulegać zmianie, ponieważ tłumienie przeciwstawia się, a więc spowalnia ruch tam i z powrotem. (Siła netto jest mniejsza w obu kierunkach). Jeśli tłumienie jest bardzo duże, układ nawet nie drga – powoli zmierza do równowagi. Częstotliwość kątowa jest równa

Wraz ze wzrostem b, \frac{k}{m}-{(\frac{b}{2m})}^{2} staje się mniejsza i ostatecznie osiąga zero, gdy b= \sqrt{4mk} . Jeśli b jest większe, to ^{k}{m}-{(^frac{b}{2m})}^{2} staje się liczbą ujemną, a ^sqrt{frac{k}{m}-{(^frac{b}{2m})}^{2}} jest liczbą złożoną.

(Rysunek) pokazuje przemieszczenie oscylatora harmonicznego dla różnych wartości tłumienia. Gdy stała tłumiąca jest mała, b<sqrt{4mk} , układ oscyluje, a amplituda ruchu maleje wykładniczo. Mówi się, że taki układ jest niedotłumiony, jak na krzywej (a). Wiele układów jest niedotłumionych i oscyluje, podczas gdy amplituda maleje wykładniczo, np. masa drgająca na sprężynie. Tłumienie może być dość małe, ale w końcu masa się zatrzymuje. Jeżeli stała tłumienia wynosi b=sqrt{4mk} , to mówi się, że układ jest krytycznie tłumiony, jak na krzywej (b). Przykładem układu krytycznie tłumionego są amortyzatory w samochodzie. Korzystne jest, aby oscylacje zanikały tak szybko jak to możliwe. W tym przypadku układ nie oscyluje, lecz asymptotycznie zbliża się do stanu równowagi tak szybko, jak to możliwe. Krzywa (c) na rysunku przedstawia układ nadmiernie wytłumiony, w którym b> ∑sqrt{4mk}. Układ nadmiernie tłumiony będzie zbliżał się do stanu równowagi w dłuższym okresie czasu.

Rysunek 15.27 Położenie w funkcji czasu dla trzech układów składających się z masy i sprężyny w lepkiej cieczy. (a) Jeżeli tłumienie jest małe (b< ), masa oscyluje, powoli tracąc amplitudę, ponieważ energia jest rozpraszana przez siłę(y) niekonserwatywną(e). Przypadkiem granicznym jest przypadek (b), w którym tłumienie wynosi (b=sqrt{4mk}) . (c) Jeżeli tłumienie jest bardzo duże (b>

Tłumienie krytyczne jest często pożądane, ponieważ taki układ szybko powraca do równowagi i również pozostaje w równowadze. Ponadto, stała siła przyłożona do układu z tłumieniem krytycznym powoduje przesunięcie układu do nowego położenia równowagi w możliwie najkrótszym czasie bez przekroczenia lub oscylacji wokół nowego położenia.

Sprawdź swoje zrozumienie

Dlaczego całkowicie nietłumione oscylatory harmoniczne są tak rzadkie?

Pokaż rozwiązanie

Tarcie często wchodzi w grę, gdy obiekt jest w ruchu. Tarcie powoduje tłumienie w oscylatorze harmonicznym.

Podsumowanie

• Tłumione oscylatory harmoniczne mają niekonserwatywne siły, które rozpraszają ich energię.
• Tłumienie krytyczne powoduje powrót układu do stanu równowagi tak szybko, jak to możliwe, bez przekroczenia punktu równowagi.
• Układ niedostatecznie wytłumiony będzie oscylował przez położenie równowagi.
• Układ nadmiernie wytłumiony porusza się wolniej w kierunku równowagi niż taki, który jest krytycznie wytłumiony.

Pytania koncepcyjne

Podaj przykład wytłumionego oscylatora harmonicznego. (Są one bardziej powszechne niż nietłumione lub proste oscylatory harmoniczne.)

Pokaż rozwiązanie

Amortyzator samochodowy.

Jak samochód odbiłby się po uderzeniu w każdym z tych warunków?

(a) overdamping

(b) underdamping

(c) critical damping

Większość oscylatorów harmonicznych jest tłumiona i, jeśli nie są wysterowane, w końcu się zatrzymują. Dlaczego?

Pokaż rozwiązanie

Drugie prawo termodynamiki mówi, że perpetuum mobile jest niemożliwe. W końcu uporządkowany ruch układu maleje i wraca do stanu równowagi.

Problemy

Amplituda lekko tłumionego oscylatora maleje o 3,0% podczas każdego cyklu. Jaki procent energii mechanicznej oscylatora jest tracony w każdym cyklu?

Pokaż rozwiązanie

9%

Glossary

krytycznie tłumiony stan, w którym tłumienie oscylatora powoduje jego możliwie szybki powrót do położenia równowagi bez oscylowania tam i z powrotem wokół tego położenia naturalna częstotliwość kątowa częstotliwość kątowa układu oscylującego w SHM stan nadmiernie wytłumiony, w którym tłumienie oscylatora powoduje jego powrót do równowagi bez oscylacji; oscylator porusza się wolniej w kierunku równowagi niż w systemie krytycznie tłumionym stan niedotłumiony, w którym tłumienie oscylatora powoduje, że amplituda oscylacji tłumionego oscylatora harmonicznego zmniejsza się w czasie, ostatecznie zbliżając się do zera