⇐ Poprzedni temat|Następny temat ⇒ Spis treści
Przed przeprowadzeniem eksperymentu należy wykonać analizę mocy, aby oszacować liczbę obserwacji potrzebną do uzyskania dużej szansy na wykrycie poszukiwanego efektu.
Wprowadzenie
Podczas projektowania eksperymentu dobrze jest oszacować wielkość próby, która będzie potrzebna. Jest to szczególnie ważne, jeśli proponujesz wykonanie czegoś bolesnego dla ludzi lub innych kręgowców, gdzie szczególnie ważne jest zminimalizowanie liczby osobników (bez uczynienia próby tak małej, że cały eksperyment będzie stratą czasu i cierpienia), lub jeśli planujesz bardzo czasochłonny lub kosztowny eksperyment. Dla wielu testów statystycznych opracowano metody pozwalające oszacować wielkość próby potrzebnej do wykrycia określonego efektu lub oszacować wielkość efektu, który można wykryć przy określonej wielkości próby.
Aby przeprowadzić analizę mocy, należy określić wielkość efektu. Jest to wielkość różnicy między hipotezą zerową a hipotezą alternatywną, którą mamy nadzieję wykryć. W przypadku stosowanych i klinicznych badań biologicznych może istnieć bardzo konkretna wielkość efektu, który chcemy wykryć. Na przykład, jeśli testujesz nowy szampon dla psów, dział marketingu w Twojej firmie może Ci powiedzieć, że produkcja nowego szamponu będzie opłacalna tylko wtedy, gdy sprawi, że sierść psów będzie średnio o co najmniej 25% bardziej błyszcząca. Byłaby to wielkość efektu i używałbyś jej przy podejmowaniu decyzji, ile psów musiałbyś przepuścić przez reflektometr dla psów.
Prowadząc podstawowe badania biologiczne, często nie wiesz, jak dużej różnicy szukasz, i pokusą może być użycie największej próbki, na jaką cię stać, lub użycie próbki o podobnej wielkości do innych badań w twojej dziedzinie. Powinieneś jednak przeprowadzić analizę mocy przed przeprowadzeniem eksperymentu, aby zorientować się, jakiego rodzaju efekty mógłbyś wykryć. Na przykład, niektórzy antyszczepionkowcy zaproponowali, aby rząd Stanów Zjednoczonych przeprowadził duże badanie nieszczepionych i szczepionych dzieci, aby sprawdzić, czy szczepionki powodują autyzm. Nie jest jasne, jaka wielkość efektu byłaby interesująca: 10% więcej autyzmu w jednej grupie? 50% więcej? dwa razy więcej? Jednak analiza mocy pokazuje, że nawet jeśli badanie objęłoby każde nieszczepione dziecko w Stanach Zjednoczonych w wieku od 3 do 6 lat i taką samą liczbę dzieci szczepionych, musiałoby być o 25% więcej autyzmu w jednej grupie, aby istniała duża szansa na zaobserwowanie znaczącej różnicy. Bardziej wiarygodne badanie, obejmujące 5000 nieszczepionych i 5000 szczepionych dzieci, wykryłoby znaczącą różnicę przy wysokiej mocy tylko wtedy, gdyby w jednej grupie było trzy razy więcej autyzmu niż w drugiej. Ponieważ jest mało prawdopodobne, że istnieje tak duża różnica w autyzmie między dziećmi szczepionymi i nieszczepionymi, i ponieważ brak znalezienia związku w takim badaniu nie przekonałby antyszczepionkowców, że nie ma żadnego związku (nic nie przekonałoby ich, że nie ma żadnego związku – to właśnie czyni z nich kokainistów), analiza mocy mówi, że tak duże, kosztowne badanie nie byłoby warte zachodu.
Parametry
W analizie mocy bierze udział cztery lub pięć liczb. Musisz wybrać wartości dla każdej z nich przed wykonaniem analizy. Jeśli nie masz dobrego powodu, aby użyć konkretnej wartości, możesz wypróbować różne wartości i sprawdzić wpływ na wielkość próby.
Wielkość efektu
Wielkość efektu to minimalne odchylenie od hipotezy zerowej, które masz nadzieję wykryć. Na przykład, jeśli leczysz kury czymś, co masz nadzieję zmieni stosunek płci ich piskląt, możesz zdecydować, że minimalna zmiana w proporcji płci, której szukasz, wynosi 10%. Można by wtedy powiedzieć, że wielkość efektu wynosi 10%. Jeśli testujesz coś, co sprawi, że kury będą znosić więcej jaj, wielkość efektu może wynosić 2 jaja miesięcznie.
Okresowo, będziesz miał dobry ekonomiczny lub kliniczny powód do wyboru określonej wielkości efektu. Jeśli testujesz dodatek do paszy dla kurcząt, który kosztuje 1,50$ miesięcznie, interesuje cię tylko to, czy będzie on produkował więcej niż 1,50$ dodatkowych jaj każdego miesiąca; wiedza, że dodatek produkuje dodatkowe 0,1 jajka miesięcznie nie jest dla ciebie użyteczną informacją i nie musisz projektować eksperymentu, aby się tego dowiedzieć. Ale dla większości podstawowych badań biologicznych, wielkość efektu jest po prostu ładną okrągłą liczbą, którą wyciągnąłeś z tyłka. Powiedzmy, że przeprowadzasz analizę mocy dla badań nad mutacją w regionie promotora, aby sprawdzić, czy wpływa ona na ekspresję genu. Jak dużej zmiany w ekspresji genów szukasz: 10%? 20%? 50%? To dość arbitralna liczba, ale będzie miała ogromny wpływ na liczbę transgenicznych myszy, które oddadzą swoje drogie, małe życia za twoją naukę. Jeśli nie masz dobrego powodu, by szukać określonej wielkości efektu, możesz równie dobrze przyznać się do tego i narysować wykres z wielkością próby na osi X i wielkością efektu na osi Y. G*Power zrobi to za Ciebie.
Alfa
Alfa to poziom istotności testu (wartość P), prawdopodobieństwo odrzucenia hipotezy zerowej, nawet jeśli jest ona prawdziwa (fałszywy wynik pozytywny). Zwykła wartość to alfa=0.05. Niektóre kalkulatory mocy używają alfa jednoogonowego, co jest mylące, ponieważ alfa dwuogonowe jest znacznie bardziej powszechne. Upewnij się, że wiesz, którego używasz.
Beta lub moc
Beta, w analizie mocy, jest prawdopodobieństwem przyjęcia hipotezy zerowej, nawet jeśli jest ona fałszywa (fałszywie ujemna), gdy rzeczywista różnica jest równa minimalnej wielkości efektu. Moc testu to prawdopodobieństwo odrzucenia hipotezy zerowej (uzyskania istotnego wyniku), gdy rzeczywista różnica jest równa minimalnej wielkości efektu. Moc jest równa 1-beta. Nie ma wyraźnego konsensusu co do wartości, którą należy zastosować, więc jest to kolejna liczba, którą wyciągasz z tyłka; moc 80% (równoważna z betą 20%) jest prawdopodobnie najbardziej powszechna, podczas gdy niektórzy używają 50% lub 90%. Koszt fałszywego wyniku negatywnego powinien mieć wpływ na wybór mocy; jeśli naprawdę chcesz być pewien, że wykryjesz wielkość efektu, będziesz chciał użyć wyższej wartości mocy (niższej bety), co spowoduje większą wielkość próby. Niektóre kalkulatory mocy proszą o podanie wartości beta, podczas gdy inne proszą o podanie wartości mocy (1-beta); należy być bardzo pewnym, że rozumie się, której wartości należy użyć.
Odchylenie standardowe
Dla zmiennych pomiarowych, potrzebujesz również oszacowania odchylenia standardowego. Gdy odchylenie standardowe staje się większe, trudniej jest wykryć znaczącą różnicę, więc będziesz potrzebował większej wielkości próby. Twoje oszacowanie odchylenia standardowego może pochodzić z eksperymentów pilotażowych lub z podobnych eksperymentów w opublikowanej literaturze. Jest mało prawdopodobne, że po przeprowadzeniu eksperymentu Twoje odchylenie standardowe będzie dokładnie takie samo, więc Twój eksperyment będzie w rzeczywistości nieco bardziej lub mniej silny niż przewidywałeś.
Dla zmiennych nominalnych odchylenie standardowe jest prostą funkcją wielkości próby, więc nie musisz go osobno szacować.
Jak to działa
Szczegóły analizy mocy są różne dla różnych testów statystycznych, ale podstawowe koncepcje są podobne; tutaj użyję dokładnego testu dwumianowego jako przykładu. Wyobraź sobie, że badasz złamania nadgarstków i twoja hipoteza zerowa brzmi, że połowa ludzi, którzy łamią jeden nadgarstek łamie prawy nadgarstek, a połowa lewy. Decydujesz, że minimalna wielkość efektu wynosi 10%; jeśli odsetek osób, które łamią prawy nadgarstek wynosi 60% lub więcej, lub 40% lub mniej, chcesz mieć znaczący wynik z dokładnego testu dwumianowego. Nie mam pojęcia, dlaczego wybrałeś 10%, ale to jest to, czego użyjesz. Alfa wynosi 5%, jak zwykle. Chcesz, aby moc wynosiła 90%, co oznacza, że jeśli odsetek złamanych prawych nadgarstków naprawdę wynosi 40% lub 60%, chcesz mieć wielkość próbki, która przyniesie znaczący (P<0,05) wynik 90% czasu, a nieistotny wynik (który byłby fałszywym negatywem w tym przypadku) tylko 10% czasu.
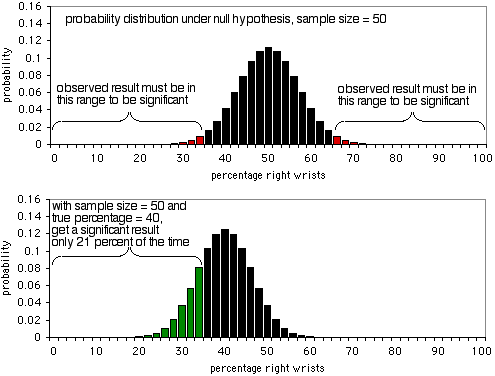

Pierwszy wykres przedstawia rozkład prawdopodobieństwa przy hipotezie zerowej, przy liczebności próby 50 osób. Jeśli hipoteza zerowa jest prawdziwa, zobaczysz mniej niż 36% lub więcej niż 64% ludzi łamiących prawe nadgarstki (fałszywy wynik pozytywny) około 5% czasu. Jak pokazuje drugi wykres, jeśli prawdziwy procent wynosi 40%, dane z próbki będą mniejsze niż 36 lub większe niż 64% tylko przez 21% czasu; prawdziwy wynik pozytywny otrzymamy tylko przez 21% czasu, a fałszywy wynik negatywny przez 79% czasu. Oczywiście, próbka o wielkości 50 jest zbyt mała dla tego eksperymentu; przyniosłaby znaczący wynik tylko w 21% przypadków, nawet jeśli stosunek złamanych prawych nadgarstków do lewych wynosi 40:60.
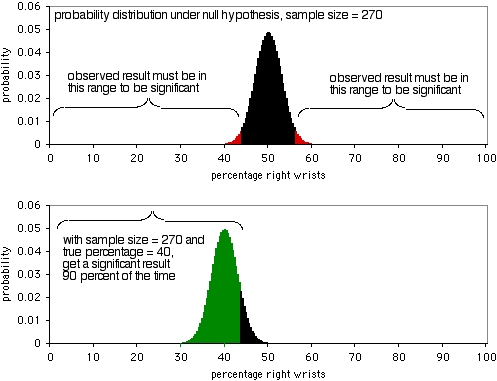

Następny wykres przedstawia rozkład prawdopodobieństwa przy hipotezie zerowej, przy liczebności próby 270 osób. Aby obserwowany wynik był istotny na poziomie P<0,05, musiałoby być mniej niż 43,7% lub więcej niż 56,3% osób łamiących prawe nadgarstki. Jak pokazuje drugi wykres, jeśli prawdziwy procent wynosi 40%, dane z próbki będą tak skrajne przez 90% czasu. Próbka o wielkości 270 jest całkiem dobra dla tego eksperymentu; przyniosłaby znaczący wynik w 90% przypadków, gdyby stosunek złamanych prawych nadgarstków do lewych wynosił 40:60. Jeśli stosunek złamanych prawych do lewych nadgarstków jest bardziej oddalony od 50:50, będziesz miał jeszcze większe prawdopodobieństwo uzyskania znaczącego wyniku.
Przykłady
Planujesz skrzyżować groch, który jest heterozygotą dla żółtego/zielonego koloru grochu, gdzie żółty jest dominujący. Oczekiwana proporcja u potomstwa to 3 żółte: 1 zielony. Chcesz wiedzieć, czy żółty groch jest w rzeczywistości bardziej lub mniej dopasowany, co może objawiać się jako inna proporcja żółtego grochu niż oczekiwana. Arbitralnie zdecydowałeś, że chcesz mieć wielkość próby, która wykryje znaczącą (P<0.05) różnicę, jeśli jest 3% więcej lub mniej żółtego groszku niż oczekiwano, z mocą 90%. Przetestujesz dane za pomocą dokładnego testu dwumianowego dobroci dopasowania, jeśli wielkość próby jest wystarczająco mała, lub testu G dobroci dopasowania, jeśli wielkość próby jest większa. Analiza mocy jest taka sama dla obu testów.
Używając G*Power, jak opisano dla dokładnego testu dobroci dopasowania, wynik jest taki, że potrzeba 2109 roślin grochu, jeśli chcesz uzyskać znaczący (P<0.05) wynik 90% czasu, jeśli prawdziwa proporcja żółtego grochu wynosi 78%, a 2271 grochu, jeśli prawdziwa proporcja wynosi 72% żółtego. Ponieważ byłbyś zainteresowany odchyleniem w obu kierunkach, używasz większej liczby, 2271. To dużo grochu, ale uspokajamy się, że nie jest to liczba niedorzeczna. Jeśli chcesz wykryć różnicę 0,1% między oczekiwaną a obserwowaną liczbą żółtych groszków, możesz obliczyć, że będziesz potrzebował 1 970 142 groszków; jeśli to jest to, co musisz wykryć, analiza wielkości próbki mówi Ci, że będziesz musiał uwzględnić robota sortującego groszek w swoim budżecie.
Przykładowe dane dla dwupróbkowego testu t pokazują, że średni wzrost w sekcji 2 p.m. Biologicznej Analizy Danych wynosił 66,6 cala, a średni wzrost w sekcji 5 p.m. wynosił 64,6 cala, ale różnica nie jest znacząca (P=0,207). Chcesz wiedzieć, ilu uczniów musiałbyś przebadać, aby mieć 80% szans na to, że tak duża różnica będzie znacząca. Używając programu G*Power, tak jak to opisano na stronie poświęconej testowi t dla dwóch prób, wpisz 2.0 dla różnicy średnich. Używając funkcji STDEV w Excelu, oblicz odchylenie standardowe dla każdej próbki w oryginalnych danych; wynosi ono 4,8 dla próbki 1 i 3,6 dla próbki 2. Wprowadź 0,05 dla alfa i 0,80 dla mocy. Wynik to 72, co oznacza, że jeśli uczniowie z godziny 17.00 naprawdę byli o dwa cale niżsi niż uczniowie z godziny 14.00, potrzeba 72 uczniów w każdej klasie, aby wykryć znaczącą różnicę w 80% przypadków, jeśli prawdziwa różnica naprawdę wynosi 2,0 cale.
Jak przeprowadzać analizy mocy
G*Power
G*Power jest doskonałym darmowym programem, dostępnym dla Maca i Windows, który przeprowadza analizy mocy dla wielu różnych testów. Wyjaśnię, jak używać G*Power do analizy mocy dla większości testów w tym podręczniku.
R
Salvatore Mangiafico’s R Companion ma przykładowe programy R do wykonywania analiz mocy dla wielu testów w tym podręczniku; przejdź do strony poświęconej poszczególnym testom i przewiń na sam dół, aby znaleźć program do analizy mocy.
SAS
SAS ma PROC POWER, który można wykorzystać do analiz mocy. Wprowadzasz potrzebne parametry (które różnią się w zależności od testu) i wprowadzasz okres (który symbolizuje brakujące dane w SAS) dla parametru, który rozwiązujesz (zazwyczaj ntotal, całkowita wielkość próby lub npergroup, liczba prób w każdej grupie). Uważam, że G*Power jest łatwiejszy w użyciu niż SAS do tego celu, więc nie zalecam używania SAS do analiz mocy.
⇐ Poprzedni temat|Następny temat ⇒ Spis treści
Ta strona została ostatnio zmieniona 20 lipca 2015. Jej adres to http://www.biostathandbook.com/power.html. Może być cytowana jako:
McDonald, J.H. 2014. Handbook of Biological Statistics (3rd ed.). Sparky House Publishing, Baltimore, Maryland. Ta strona internetowa zawiera treść stron 40-44 w wersji drukowanej.
©2014 by John H. McDonald. Prawdopodobnie możesz zrobić z tą treścią, co chcesz; zobacz stronę z zezwoleniami, aby uzyskać szczegółowe informacje.