Równanie Darcy’ego-Weisbacha, do obliczania strat tarcia w rurze, używa bezwymiarowej wartości znanej jako współczynnik tarcia (znany również jako współczynnik tarcia Darcy’ego-Weisbacha lub współczynnik tarcia Moody’ego) i jest on cztery razy większy niż współczynnik tarcia Fanninga.
Wykres współczynnika tarcia / wykres Moody’ego
Wykres współczynnika tarcia lub wykres Moody’ego jest wykresem względnej chropowatości (e/D) rury względem liczby Reynolda. Niebieskie linie wykreślają współczynnik tarcia dla przepływu w całkowicie turbulentnym obszarze wykresu, podczas gdy prosta czarna linia wykreśla współczynnik tarcia dla przepływu w całkowicie laminarnym obszarze wykresu.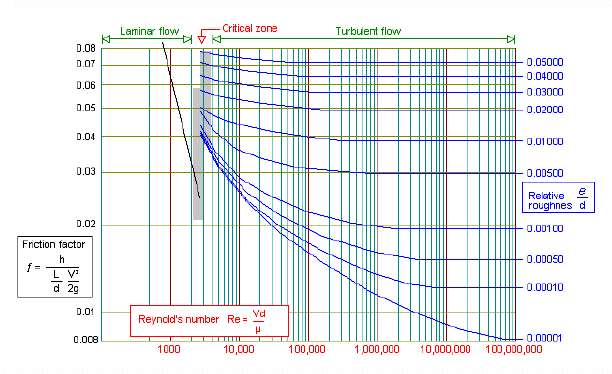
W 1944 roku LF Moody wykreślił dane z równania Colebrooka, a uzyskany wykres stał się znany jako wykres Moody’ego lub czasami jako wykres współczynnika tarcia. To właśnie ten wykres po raz pierwszy umożliwił użytkownikowi uzyskanie w miarę dokładnego współczynnika tarcia dla warunków przepływu turbulentnego, w oparciu o liczbę Reynoldsa i względną chropowatość rury.
Współczynnik tarcia dla przepływu laminarnego
Współczynnik tarcia dla przepływu laminarnego jest obliczany poprzez podzielenie 64 przez liczbę Reynoldsa.
Współczynnik tarcia (dla przepływu laminarnego) = 64 / Re
Przepływ krytyczny
Gdy przepływ występuje pomiędzy warunkami przepływu laminarnego i turbulentnego (Re 2300 do Re 4000), stan przepływu jest znany jako krytyczny i jest trudny do przewidzenia. W tym przypadku przepływ nie jest ani w pełni laminarny, ani w pełni turbulentny. Jest to kombinacja tych dwóch warunków przepływu.
Współczynnik tarcia dla przepływu turbulentnego
Współczynnik tarcia dla przepływu turbulentnego jest obliczany przy użyciu równania Colebrooka-White’a:
Równanie Colebrooka-White’a
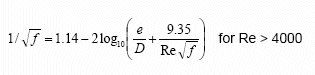
Z uwagi na niejawne tworzenie równania Colebrooka-White’a, obliczenie współczynnika tarcia wymaga iteracyjnego rozwiązania za pomocą metod numerycznych.
Współczynnik tarcia jest następnie wykorzystywany we wzorze Darcy’ego-Weisbacha do obliczania strat spowodowanych tarciem cieczy w rurze.