Heading

W roku 1072 n.e. Omar Khayyam udokumentował najdokładniejszą długość roku, jaką kiedykolwiek obliczono – liczba ta jest nadal wystarczająco dokładna dla większości celów we współczesnym świecie. Khayyam był astronomem, astrologiem, lekarzem, filozofem i matematykiem: wniósł wybitny wkład w algebrę. Jego poezja jest lepiej znana na Zachodzie niż jakikolwiek inny poeta spoza Zachodu.

Sam człowiek pozostaje czymś w rodzaju enigmy. Różni biografowie opisują go jako lubiącego zabawę, pijącego wino agnostyka, zoroastrianina, sufickiego muzułmanina, ortodoksyjnego sunnitę i wyznawcę starożytnej filozofii greckiej. Wszyscy zgadzają się, że był on wybitnym intelektualistą.

Początki

Omar Khayyam urodził się 18 maja 1048 roku w wielkim mieście handlowym Nishapur w północnej Persji. Dziś miasto to znajduje się w Iranie. Ojcem Omara był Ebrahim Khayyami, bogaty lekarz. Imię matki Omara nie jest znane. Niektórzy autorzy piszą, że ojciec Omara zarabiał na życie produkując namioty, ponieważ Khayyami oznacza twórcę namiotów. Jednak, choć wielu Anglików nosi nazwisko Smith, nie oznacza to, że ich ojcowie spędzali całe dnie na młotkowaniu gorącego metalu na kowadle.

Rodzina Omara była muzułmanami. Jego ojciec był zrelaksowany w kwestii religii, zatrudniając matematyka Bahmanyara bin Marzbana, wyznawcę starożytnej perskiej religii zoroastryzmu, jako nauczyciela Omara. Bahmanyar był uczniem wielkiego lekarza, naukowca i filozofa Awicenny i przekazał Omarowi gruntowne wykształcenie w dziedzinie nauki, filozofii i matematyki. Khawjah al-Anbari uczył Omara astronomii, prowadząc go przez Almagest Ptolemeusza.

W wieku kilkunastu lat Omar pracował w gabinecie ojca, ucząc się medycyny.

Omar Khayyam obchodził osiemnaste urodziny w 1066 roku. W tym samym roku na niebie pojawiła się kometa Halleya, armia normańska Wilhelma Zdobywcy najechała Anglię, a ojciec Omara, Ebrahim, zmarł. Kilka miesięcy po śmierci Ebrahima zmarł również nauczyciel Omara, Bahmanyar.

To był koniec pewnej ery w życiu Omara Khayyama. Nadszedł czas, by uporządkować sprawy rodzinne i ruszyć w dalszą drogę.

Samarkanda

Omar Khayyam dołączył do jednej z regularnych karawan odbywających trzymiesięczną podróż z Nishapuru do wielkiego miasta Samarkandy, które obecnie znajduje się w Uzbekistanie. Samarkanda była centrum nauki, a Khayyam przybył tam prawdopodobnie w 1068 roku, w wieku 20 lat.

W Samarkandzie nawiązał kontakt ze starym przyjacielem swojego ojca, Abu Tahirem, który był gubernatorem i głównym sędzią miasta. Tahir, dostrzegając niezwykły talent Khayyama do liczb, dał mu pracę w swoim biurze. Wkrótce Khayyam otrzymał posadę w królewskim skarbcu.

Podczas pobytu w Samarkandzie Khayyam dokonał znacznego postępu w algebrze.

Wkład Omara Khayyama do nauki

Algebra

W szkole średniej uczymy się o równaniach w postaci ax2 + bx + c = 0; nazywamy je równaniami kwadratowymi. Równania sześcienne mają postać ax3 + bx2 + cx + d = 0. Naturalnie, równania sześcienne są trudniejsze do rozwiązania niż czworokątne.

Khayyam słusznie przypuszczał, że nie jest możliwe rozwiązywanie równań sześciennych za pomocą tradycyjnych starożytnych greckich narzędzi geometrycznych: liniału i kompasu. Konieczne są inne metody.

W wieku 22 lat, w 1070 roku, Khayyam opublikował jedno ze swoich największych dzieł: Treatise on Demonstration of Problems of Algebra and Balancing. Pokazał w nim, że równanie sześcienne może mieć więcej niż jedno rozwiązanie. Pokazał również, jak można wykorzystać przecięcia odcinków stożkowych, takich jak parabole i okręgi, do uzyskania geometrycznych rozwiązań równań sześciennych. Archimedes rozpoczął prace w tej dziedzinie ponad tysiąc lat wcześniej, kiedy rozważał problem znalezienia stosunku objętości jednej części kuli do drugiej. Khayyam rozpatrywał ten problem w sposób bardziej ogólny, metodyczny.

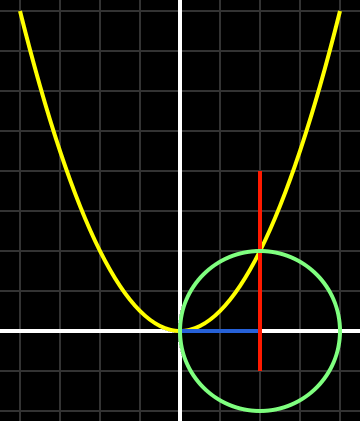
W języku współczesnej matematyki rozwiązanie Khayyama równania x3 + a2x = b zawiera parabolę o równaniu x2 = ay, okrąg o średnicy b/a2 oraz pionową linię przechodzącą przez punkt przecięcia. Rozwiązanie jest określone przez odległość na osi x między początkiem a (czerwoną) linią pionową. Obraz autorstwa Pietera Kuipera.

W rozwiązaniach Khayyama unikano ujemnych współczynników i ujemnych pierwiastków, ponieważ liczby ujemne nie były uznawane w matematyce islamskiej. (Niektóre kultury, jednakże, włączyły liczby ujemne do matematyki – na przykład Brahmagupta wprowadził liczby ujemne do matematyki indyjskiej 400 lat wcześniej.)

Ale osiągnięcie Khayyama było wspaniałe, był on osobiście rozczarowany, że musiał użyć geometrii do rozwiązania równań sześciennych – miał nadzieję odkryć algorytm używając tylko algebry.

Traktat o demonstracji problemów algebry i równowagi ustanowił Khayyama matematykiem pierwszej rangi, a jego reputacja szybko rozprzestrzeniła się w całej Persji.

Po przełomie Chajjama nastąpił niewielki postęp w dziedzinie równań sześciennych aż do 1535 roku, kiedy Niccolo Tartaglia znalazł ogólne rozwiązania wszystkich równań sześciennych.

Algebra Chajjama nie była systemem liter i znaków, którego używamy dzisiaj. Jego algebra była wyrażona w słowach. Tak więc tam, gdzie dziś piszemy:

Rozwiąż dla x:

x2 + 6 = 5x

Khayyam napisał: Ile wynosi taki kwadrat, że po dodaniu do niego 6 dirhamów staje się on równy pięciu pierwiastkom z tego kwadratu?

Połączenie algebry i geometrii

Algebra i geometria zostały z powodzeniem połączone przez Pierre’a de Fermata i René Descartes’a w latach 1600, co zaowocowało nowoczesnym układem współrzędnych x-y.

Praca Khayyama z kubikami upewniła go, że algebra i geometria są powiązane, i zacytował on Elementy Euklidesa, aby poprzeć ten pomysł:

Ktokolwiek myśli, że algebra jest sztuczką w uzyskiwaniu niewiadomych, myśli na próżno. Nie należy zwracać uwagi na to, że algebra i geometria różnią się wyglądem. Algebry są faktami geometrycznymi, których dowodzą twierdzenia 5 i 6 z księgi drugiej Elementów Euklidesa.

Długość roku

W 1073 r. Khayyam otrzymał zaproszenie do perskiego miasta Isfahan, stolicy imperium Seldżuków, aby przygotować kalendarz, który działałby w sposób uporządkowany i byłby dokładny na zawsze – była to epoka, w której regularnie zmieniano długości lat.

Zaproszenie Chajjama pochodziło od dwóch najpotężniejszych ludzi w imperium Seldżuków, którego częścią była Persja: byli to Malik Szah, sułtan imperium, i Nizam al-Mulk, jego wezyr.

Khayyam zwerbował innych utalentowanych naukowców, by towarzyszyli mu w Isfahanie w 1074 roku. Tam otrzymał niezwykle wysoką pensję i cieszył się uprzywilejowanym stylem życia. Malik Shah zapłacił Khayyamowi za założenie obserwatorium, którego początkowym celem było prowadzenie obserwacji nieba przez 30 lat, w czasie których Saturn, najodleglejsza znana wówczas planeta, miał zakończyć orbitę.

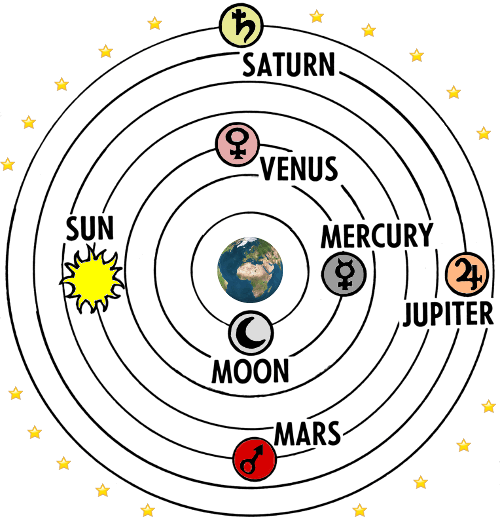
Wszechświat Ptolemeusza – model przyjęty przez Omara Khayyama.

Podczas pobytu w Isfahanie, Khayyam zmierzył długość roku – a konkretnie długość roku zwrotnikowego – z niezwykłą dokładnością i precyzją.

Khayyam stwierdził, że 1,029,983 dni składa się na 2,820 lat. Daje to długość roku zwrotnikowego równą 365,2422 dni z dokładnością do siedmiu cyfr znaczących. Chociaż modne stało się podawanie większej liczby miejsc po przecinku niż ta, podana przez Khayyama liczba 1,029,983 dni zawiera siedem cyfr znaczących, więc nie ma sensu podawać więcej niż ta liczba cyfr znaczących w wyliczonej długości roku.

Dzisiaj wiemy, że długość roku zwrotnikowego zmienia się w rzeczywistości aż o 30 minut z roku na rok. Średnia podawana dziś długość roku zwrotnikowego wynosi 365,242189 dnia, co przy siedmiu cyfrach znaczących daje 365,2422 dnia – dokładnie taką samą liczbę, do jakiej doszedł Chajjam prawie tysiąc lat temu. Długość roku zwrotnikowego również nieznacznie wzrasta w miarę upływu czasu, choć nie na tyle między erą Khayyama a naszą, by było to zauważalne w skali siedmiu cyfr znaczących.

Malik Shah wprowadził nowy kalendarz Khayyama w Imperium Seldżuków 15 marca 1079 roku. Był on używany aż do XX wieku.

Postulat równoległości

13 ksiąg Elementów Euklidesa opublikowanych w około 300 roku p.n.e. było prawdopodobnie najbardziej wpływowymi książkami w całej historii matematyki. Elementy zostały zbudowane na pięciu postulatach geometrycznych – innymi słowy, pięciu rzeczach, które uznano za prawdziwe w geometrii: na przykład, że wszystkie kąty proste są sobie równe.

Piątym z pięciu postulatów Euklidesa był postulat równoległości. Postulat równoległości przez tysiąclecia był dla matematyków źródłem zdziwienia, irytacji i radości. Radość była zwykle krótkotrwała, należała do matematyków, którzy myśleli, że udowodnili postulat, a potem rozczarowali się, gdy w ich „dowodzie” znaleziono błąd.

Euklides rozważał linię prostą przecinającą dwie inne linie proste. Przyjrzał się sytuacji, gdy kąty wewnętrzne (pokazane na poniższym rysunku) sumują się do mniej niż 180 stopni. W takich okolicznościach stwierdził, że dwie proste ostatecznie spotkają się po stronie dwóch kątów, które sumują się do mniej niż 180 stopni.

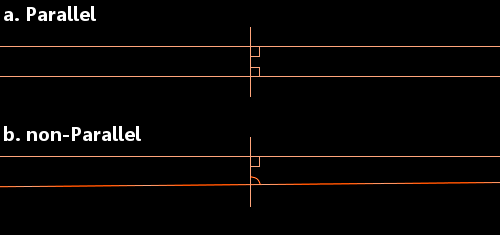
a. Gdy każdy z kątów ma 90 stopni, to proste są równoległe.
b. Jeżeli jeden lub oba kąty są mniejsze niż 90 stopni, to proste się spotkają.

Od czasu opublikowania Elementów matematycy próbowali wykorzystać pierwsze cztery postulaty Euklidesa do udowodnienia postulatu równoległości. Byli skazani na porażkę. Teraz wiemy, że nie da się udowodnić postulatu równoległości za pomocą innych postulatów Euklidesa.

Próba Omara Khayyama była interesująca. W swoich Objaśnieniach trudności w postulatach z Elementów Euklidesa prosi czytelników, by rozważyli prostą AB:

Poprosił czytelników, by rozważyli dwie równe proste prostopadłe do AB i widzi trzy możliwe układy, które mogą dać figury czteroboczne:

Potem odrzuca możliwość, że kąty C i/lub D mogą być czymkolwiek innym niż kątami prostymi, a na powyższym obrazku tylko środkowa opcja jest możliwa. Uważa więc, że udowodnił postulat równoległości. W rzeczywistości, nie zrobił tego, wszystko co zrobił to stwierdził to w inny sposób.

Co jest interesujące dla historyków matematyki to fakt, że w pomysłach Khayyama – pokazanych w przybliżeniu na obrazkach powyżej – mogą oni zobaczyć pierwsze przebłyski geometrii nie-euklidesowej.

Kilka osobistych szczegółów i koniec

Pełne szczegóły życia osobistego Khayyama nie są znane. Uważa się, że był żonaty i miał co najmniej jednego syna i jedną córkę.

W 1092 roku Malik Shah i jego wezyr zmarli – pierwszy prawdopodobnie przez otrucie, drugi przez zamach. Khayyam ukrył się w czasie walki o władzę. Jego przetrwanie zależało od tego, czy się nie wychylił. Był osobistym lekarzem Malika Szacha i stał się jego bliskim przyjacielem, co przysporzyło mu wrogów, a poezja Khayyama sugeruje, że jego zachowanie mogło nie być pobożne, co również przysporzyło mu wrogów. Khayyam w rzeczywistości nie opublikował żadnej poezji za życia. Niektóre z jego rozmyślań potencjalnie zagroziłyby jego życiu.

Po walce o władzę minęło około 20 lat, zanim Khayyam został w pełni zrehabilitowany i w wieku 64 lat pojawił się ponownie w towarzystwie wpływowych ludzi. Odmówił jednak nauczania. Jeden z jego wierszy sugeruje, dlaczego tak może być:

Omar Khayyam zmarł w wieku 83 lat w swoim rodzinnym mieście Nishapur 4 grudnia 1131 roku. Został pochowany w wybranym przez siebie grobowcu w sadzie, w którym dwa razy do roku opadały kwiaty.

Poezja Khayyama została spopularyzowana w 1800 roku przez przekłady Edwarda FitzGeralda w Rubajjacie Omara Khayyama. Khayyam stał się tak podziwiany na Zachodzie, że w 1963 r. szach Iranu kazał ekshumować jego grób i przenieść szczątki Khayyama do ogromnego, specjalnie wybudowanego mauzoleum w Nishapur, gdzie turyści mogli oddać hołd wielkiemu poecie.

Zakończmy jednym z najbardziej znanych i sugestywnych quatrains Khayyam’a:

Autor strony: The Doc
Obrazy cyfrowo ulepszone i pokolorowane przez tę stronę. © Wszelkie prawa zastrzeżone.

Cytuj tę stronę

Proszę użyć następującego cytatu zgodnego z MLA:

"Omar Khayyam." Famous Scientists. famousscientists.org. 5 Nov. 2016. Web. <www.famousscientists.org/omar-khayyam/>.

Published by FamousScientists.org

Dalsza lektura
Edward FitzGerald (tłumacz)
The Rubaiyat of Omar Khayyam
Howard Willford Bell, 1901

Victor J. Katz
A History of Mathematics: An Introduction
HarperCollins College Publishers, New York, 1993

Roshdi Rashed (Editor)
Encyclopedia of the History of Arabic science
Routledge, 1996

History of Astronomy – Middle East
ephemeris.com, 2003

Hazhir Teimourian
Omar Khayyam: Poet, Rebel, Astronomer
The History Press, 2008

Mehdi Aminrazavi
The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam
Oneworld Publications, 2013