Metoda mnożników Lagrange’a jest narzędziem pracy ekonomisty przy rozwiązywaniu problemów optymalizacyjnych. Technika ta jest centralnym punktem teorii ekonomii, ale niestety zazwyczaj jest źle nauczana.
Większość podręczników koncentruje się na mechanicznym wypisywaniu wzorów, pozostawiając studentów niezrozumiałych co do tego, dlaczego to właściwie działa na początku. W tym wpisie wyjaśnię prosty sposób na zobaczenie, dlaczego mnożniki Lagrange’a robią to, co robią – to znaczy, rozwiązują problemy optymalizacji z ograniczeniami poprzez użycie pół-tajemniczej funkcji Lagrangianu.
Kilka informacji
Zanim zobaczysz, dlaczego ta metoda działa, musisz wiedzieć coś o gradientach. Dla funkcji jednej zmiennej istnieje – zazwyczaj – jedna pierwsza pochodna. Dla funkcji n zmiennych, istnieje n pierwszych pochodnych. Gradient jest po prostu wektorem, który zbiera wszystkie częściowe pierwsze pochodne funkcji w jednym miejscu.
Każdy element gradientu jest jedną z częściowych pierwszych pochodnych funkcji. Łatwym sposobem myślenia o gradiencie jest to, że jeśli wybierzemy punkt na jakiejś funkcji, to daje nam to „kierunek”, w którym zmierza funkcja. Jeśli nasza funkcja jest oznaczona
notacja dla gradientu f to
Najważniejszą rzeczą, jaką należy wiedzieć o gradientach, jest to, że zawsze wskazują one w kierunku największego nachylenia funkcji w danym punkcie. Aby to zobrazować, spójrzmy na poniższy rysunek. Ilustruje on sposób działania gradientów dla funkcji dwóch zmiennych x1 i x2.
Funkcja f na rysunku tworzy wzgórze. W kierunku szczytu narysowałem dwa obszary, w których utrzymujemy stałą wysokość f na pewnym poziomie a. Nazywamy je krzywymi poziomymi f i oznaczamy f = a1 oraz f = a2.
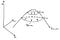
Wyobraź sobie, że stoisz na jednym z tych równych łuków. Pomyśl o szlaku turystycznym na zboczu góry. Stojąc na szlaku, w którym kierunku góra jest najbardziej stroma? Wyraźnie najbardziej stromy kierunek jest prosto w górę wzgórza, prostopadle do szlaku. Na rysunku strzałkami zaznaczono te ścieżki najbardziej stromego wzniesienia. To są nachylenia
w różnych punktach wzdłuż krzywych poziomów. Tak jak najbardziej strome wzniesienie jest zawsze prostopadłe do naszego szlaku, tak nachylenia f są zawsze prostopadłe do jego krzywych poziomicowych.
To jest kluczowa idea: krzywe poziomicowe są tam, gdzie
i
Jak działa metoda
Aby zobaczyć jak działają mnożniki Lagrange’a, spójrzmy na poniższy rysunek. Narysowałem na nim ponownie funkcję f z góry wraz z ograniczeniem g = c. Na rysunku ograniczeniem jest płaszczyzna przecinająca nasze zbocze. Narysowałem również kilka krzywych poziomych funkcji f.

Naszym celem jest wspiąć się tak wysoko na wzgórze, jak to tylko możliwe, biorąc pod uwagę, że nie możemy się poruszać wyżej niż tam, gdzie ograniczenie g = c przecina wzgórze.
Na rysunku granica, na której ograniczenie przecina funkcję, jest zaznaczona grubą linią. Wzdłuż tej linii znajdują się najwyższe punkty, które możemy osiągnąć bez przekraczania ograniczenia. To oczywiste miejsce, w którym należy zacząć szukać ograniczonego maksimum.
Wyobraźmy sobie wędrówkę od lewej do prawej po linii ograniczenia. W miarę jak nabieramy wysokości, przechodzimy przez różne krzywe poziomu f. Na rysunku zaznaczyłem dwie z nich. Wyobraźmy sobie, że na każdej krzywej poziomej sprawdzamy jej nachylenie – czyli nachylenie linii stycznej do niej – i porównujemy je z nachyleniem na ograniczeniu, na którym stoimy.
Jeśli nasze nachylenie jest większe od krzywej poziomej, możemy dotrzeć do wyższego punktu na wzgórzu, jeśli będziemy poruszać się w prawo. Jeśli nasze nachylenie jest mniejsze niż krzywa poziomu – powiedzmy, w prawo, gdzie nasza linia ograniczenia maleje – musimy cofnąć się w lewo, aby osiągnąć wyższy punkt.
Gdy osiągniemy punkt, w którym nachylenie linii ograniczenia jest równe nachyleniu krzywej poziomu, przenieśliśmy się tak wysoko, jak to możliwe. To znaczy, że osiągnęliśmy nasze ograniczone maksimum. Każdy ruch od tego punktu spowoduje, że będziemy spadać w dół. Na rysunku punkt ten jest oznaczony dużą strzałką skierowaną w stronę szczytu.
W tym punkcie krzywa poziomu f = a2 i ograniczenie mają takie samo nachylenie. Oznacza to, że są one równoległe i skierowane w tym samym kierunku. Ale jak widzieliśmy powyżej, nachylenia są zawsze prostopadłe do krzywych poziomicowych. Jeśli więc te dwie krzywe są równoległe, to ich nachylenia również muszą być równoległe.
To oznacza, że nachylenia f i g wskazują w tym samym kierunku i różnią się co najwyżej o pewien skalar. Nazwijmy ten skalar „lambda”. Mamy wtedy,
Rozwiązując dla zera, otrzymujemy
To jest warunek, który musi się spełnić, gdy osiągniemy maksimum f z zastrzeżeniem ograniczenia g = c. Teraz, jeśli jesteśmy sprytni, możemy napisać jedno równanie, które uchwyci tę ideę. W tym miejscu pojawia się znane równanie Lagrangiana:
albo bardziej jednoznacznie,
Aby zobaczyć, jak działa to równanie, obserwujemy, co się dzieje, gdy postępujemy zgodnie ze zwykłą procedurą Lagrangiana. Po pierwsze, znajdziemy trzy częściowe pierwsze pochodne L,
i ustawić je równe zero. Oznacza to, że musimy ustawić gradient L równy zero. Aby znaleźć gradient L, bierzemy trzy pochodne cząstkowe L względem x1, x2 i lambda. Następnie umieszczamy każdą z nich jako element wektora 3 x 1. To daje nam następujące wyniki:
Przypomnijmy, że mamy tutaj dwie „zasady” do przestrzegania. Po pierwsze, gradienty f i g muszą być skierowane w tym samym kierunku, lub
Po drugie, musimy spełnić nasze ograniczenie, lub
Pierwszy i drugi element gradientu L sprawiają, że pierwsza zasada jest przestrzegana. To znaczy, wymuszają
zapewniając, że gradienty f i g skierowane są w tym samym kierunku. Trzeci element gradientu L jest po prostu sztuczką mającą na celu upewnienie się, że g = c, co jest naszym ograniczeniem. W funkcji Lagrangiana, kiedy bierzemy częściową pochodną w odniesieniu do lambda, to po prostu zwraca nam z powrotem nasze oryginalne równanie ograniczenia.
W tym momencie mamy trzy równania w trzech niewiadomych. Możemy więc rozwiązać je dla optymalnych wartości x1 i x2, które maksymalizują f z zastrzeżeniem naszego ograniczenia. I gotowe.
Więc wniosek jest taki, że mnożniki Lagrange’a to tak naprawdę tylko algorytm, który znajduje miejsca, gdzie gradient funkcji wskazuje w tym samym kierunku, co gradienty jej ograniczeń, jednocześnie spełniając te ograniczenia.
Jak w większości dziedzin matematyki, kiedy już zobaczysz sedno rzeczy – w tym przypadku, że optymalizacja to tak naprawdę tylko wspinaczka po wzgórzach, którą każdy rozumie – rzeczy są o wiele prostsze, niż większość ekonomistów uważa, że są.
Więcej o