![]()
![]()

Rozkład dwumianowy daje dyskretny rozkład prawdopodobieństwa ![]() uzyskania dokładnie
uzyskania dokładnie ![]() sukcesów z
sukcesów z ![]() prób Bernoulliego (gdzie wynik każdej próby Bernoulliego jest prawdziwy z prawdopodobieństwem
prób Bernoulliego (gdzie wynik każdej próby Bernoulliego jest prawdziwy z prawdopodobieństwem ![]() i fałszywy z prawdopodobieństwem
i fałszywy z prawdopodobieństwem ![]() ). Rozkład dwumianowy jest więc dany przez
). Rozkład dwumianowy jest więc dany przez
|
(1)
|
|||
|
(2)
|
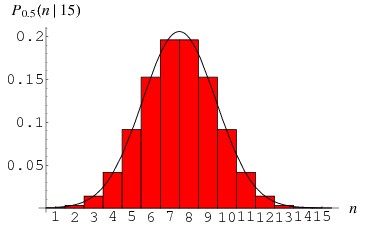
gdzie ![]() jest współczynnikiem dwumianowym. Powyższy wykres przedstawia rozkład
jest współczynnikiem dwumianowym. Powyższy wykres przedstawia rozkład ![]() sukcesów z
sukcesów z ![]() prób z
prób z ![]() .
.
Rozkład dwumianowy jest zaimplementowany w języku Wolframa jako BinomialDistribution.
Prawdopodobieństwo uzyskania większej liczby sukcesów niż ![]() obserwowane w rozkładzie dwumianowym wynosi
obserwowane w rozkładzie dwumianowym wynosi
|
(3)
|
gdzie
|
(4)
|
![]() to funkcja beta, a
to funkcja beta, a ![]() jest niekompletną funkcją beta.
jest niekompletną funkcją beta.
Funkcja charakterystyczna dla rozkładu dwumianowego wynosi
|
(5)
|
(Papoulis 1984, p. 154). Moment-Funkcja generująca moment ![]() dla tego rozkładu wynosi
dla tego rozkładu wynosi
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
Średnia wynosi
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
Momenty wokół 0 wynoszą
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
więc momenty wokół średniej są
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
Kośność i kurtoza wynoszą
|
(22)
|
|||
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
Pierwszą kumulantą jest
|
(26)
|
i kolejne kumulanty są dane przez zależność rekurencyjną
|
(27)
|
Odchylenie średnie odchylenie jest dane przez
|
(28)
|
Dla szczególnego przypadku ![]() , jest to równe
, jest to równe
|
(29)
|
|||
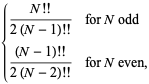 |
(30)
|
gdzie ![]() jest podwójnym czynnikiem. Dla
jest podwójnym czynnikiem. Dla ![]() , 2, …, pierwsze kilka wartości to zatem 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, …. (OEIS A086116 i A086117). Ogólny przypadek jest dany przez
, 2, …, pierwsze kilka wartości to zatem 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, …. (OEIS A086116 i A086117). Ogólny przypadek jest dany przez
|
(31)
|
Steinhaus (1999, pp. 25-28) rozważa oczekiwaną liczbę kwadratów ![]() zawierających daną liczbę ziaren
zawierających daną liczbę ziaren ![]() na tablicy o rozmiarze
na tablicy o rozmiarze ![]() po losowym rozkładzie
po losowym rozkładzie ![]() ziaren,
ziaren,
|
(32)
|
Przyjęcie ![]() daje wyniki zestawione w poniższej tabeli.
daje wyniki zestawione w poniższej tabeli.
| 0 | 23.3591 |
| 1 | 23.7299 |
| 2 | 11.8650 |
| 3 | 3.89221 |
| 4 | 0.942162 |
| 5 | 0.179459 |
| 6 | 0.0280109 |
| 7 | 0.0036840 |
| 8 | |
| 9 | |
| 10 | |
Przybliżenie do rozkładu dwumianowego dla dużych ![]() można uzyskać poprzez rozwinięcie wokół wartości
można uzyskać poprzez rozwinięcie wokół wartości ![]() gdzie
gdzie ![]() jest maksimum, i.e., gdzie
jest maksimum, i.e., gdzie ![]() . Ponieważ funkcja logarytmu jest monotoniczna, możemy zamiast tego wybrać rozwinięcie logarytmu. Niech
. Ponieważ funkcja logarytmu jest monotoniczna, możemy zamiast tego wybrać rozwinięcie logarytmu. Niech ![]() , wtedy
, wtedy
|
(33)
|
gdzie
|
(34)
|
Ale my rozszerzamy się o maksimum, więc z definicji,
|
(35)
|
To oznacza również, że ![]() jest ujemne, więc możemy napisać
jest ujemne, więc możemy napisać ![]() . Teraz, biorąc logarytm z (◇) daje
. Teraz, biorąc logarytm z (◇) daje
|
(36)
|
Dla dużych ![]() i
i ![]() możemy skorzystać z przybliżenia Stirlinga
możemy skorzystać z przybliżenia Stirlinga
|
(37)
|
Więc
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
|||
|
(41)
|
|||
|
(42)
|
i
|
(43)
|
Aby znaleźć ![]() , ustawić to wyrażenie na 0 i rozwiązać dla
, ustawić to wyrażenie na 0 i rozwiązać dla ![]() ,
,
|
(44)
|
|
(45)
|
|
(46)
|
|
(47)
|
ponieważ ![]() . Możemy teraz znaleźć wyrażenia w rozwinięciu
. Możemy teraz znaleźć wyrażenia w rozwinięciu
|
(48)
|
|||
|
(49)
|
|||
|
(50)
|
|||
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
|||
|
(55)
|
|||
|
(56)
|
|||
|
(57)
|
|||
|
(58)
|
|||
|
(59)
|
Teraz traktując rozkład jako ciągły,
|
(60)
|
Ponieważ każdy termin jest rzędu ![]() mniejszego od poprzedniego, możemy zignorować pierwiastki wyższe niż
mniejszego od poprzedniego, możemy zignorować pierwiastki wyższe niż ![]() , więc
, więc
|
(61)
|
Prawdopodobieństwo musi być znormalizowane, więc
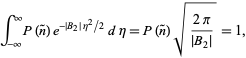 |
(62)
|
i
|
(63)
|
|||
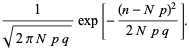 |
(64)
|
Definiowanie ![]() ,
,
|
(65)
|
który jest rozkładem normalnym. Rozkład dwumianowy jest zatem aproksymowany rozkładem normalnym dla dowolnego ustalonego ![]() (nawet jeśli
(nawet jeśli ![]() jest małe), ponieważ
jest małe), ponieważ ![]() jest przyjmowany do nieskończoności.
jest przyjmowany do nieskończoności.
Jeśli ![]() i
i ![]() w taki sposób, że
w taki sposób, że ![]() , to rozkład dwumianowy zbiega do rozkładu Poissona ze średnią
, to rozkład dwumianowy zbiega do rozkładu Poissona ze średnią ![]() .
.
Pozwólmy ![]() i
i ![]() być niezależnymi dwumianowymi zmiennymi losowymi charakteryzowanymi przez parametry
być niezależnymi dwumianowymi zmiennymi losowymi charakteryzowanymi przez parametry ![]() i
i ![]() . Prawdopodobieństwo warunkowe
. Prawdopodobieństwo warunkowe ![]() biorąc pod uwagę, że
biorąc pod uwagę, że ![]() wynosi
wynosi
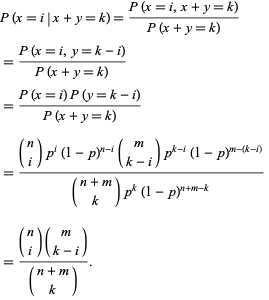 |
(66)
|
Zauważ, że jest to rozkład hipergeometryczny.