Heading

What is an Interquartile Range?

Zakres międzykwartylowy jest miarą tego, gdzie znajduje się „środkowa pięćdziesiątka” w zbiorze danych. Podczas gdy zakres jest miarą tego, gdzie początek i koniec są w zestawie, zakres międzykwartylowy jest miarą tego, gdzie leży większość wartości. Dlatego właśnie jest on preferowany w stosunku do wielu innych miar rozrzutu przy raportowaniu takich rzeczy jak wyniki szkolne lub wyniki SAT.

Wzór na zakres międzykwartylowy to pierwszy kwartyl odjęty od trzeciego kwartyla:

Zawartość (kliknij, aby przejść do sekcji strony):

Rozwiązanie ręczne:

1. Rozwiąż wzór ręcznie (nieparzysty zestaw liczb).
2. A co jeśli mam parzysty zestaw liczb?
3. Znajdź przedział międzykwartylowy dla nieparzystego zestawu liczb: Druga Metoda
4. Rozstęp międzykwartylowy na wykresie kołowym: Jak go znaleźć

Używanie technologii:

1. Rozstęp międzykwartylowy w programie Minitab
2. Rozstęp międzykwartylowy w programie Excel
3. Rozstęp międzykwartylowy w programie SPSS
4. Rozstęp międzykwartylowy w programie TI83
5. Q1, Q3 i IQR w programie TI89

Informacje ogólne:

1. Co to jest przedział międzykwartylowy?
2. Co to jest wzór na przedział międzykwartylowy?
3. IQR jako test na rozkład normalny
4. Do czego służy przedział międzykwartylowy?
5. Historia przedziału międzykwartylowego.

Rozwiąż wzór ręcznie.

Zobacz film lub przeczytaj kroki poniżej. Jeśli nadal masz trudności, skorzystaj z pomocy korepetytorów na Chegg.com. Twoje pierwsze 30 minut jest darmowe!

Kroki:

• Krok 1: Ułóż liczby w kolejności.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
• Krok 2: Znajdź medianę.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
• Krok 3: Umieść nawiasy wokół liczb powyżej i poniżej mediany.
  Nie jest to konieczne statystycznie, ale ułatwia zauważenie Q1 i Q3.
  (1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27).
• Krok 4: Znajdź Q1 i Q3
  Pomyśl o Q1 jako o medianie w dolnej połowie danych i pomyśl o Q3 jako o medianie dla górnej połowy danych.
  (1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27). Q1 = 5 i Q3 = 18.
• Krok 5: Odejmij Q1 od Q3, aby znaleźć przedział międzykwartylowy.
  18 – 5 = 13.

Podoba Ci się wyjaśnienie? Sprawdź podręcznik Practically Cheating Statistics Handbook, który zawiera setki innych wyjaśnień krok po kroku, takich jak to!

Co jeśli mam parzysty zestaw liczb?

Przykładowe pytanie: Znajdź IQR dla następującego zbioru danych: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.

• Krok 1: Ułóż liczby w kolejności.
  3, 5, 7, 8, 9, 11, 15, 16, 20, 21.
• Krok 2: Zrób znak w środku danych:
  3, 5, 7, 8, 9, | 11, 15, 16, 20, 21.
• Krok 3: Umieść nawiasy wokół liczb powyżej i poniżej znaku, który zrobiłeś w kroku 2. Dzięki temu Q1 i Q3 będą łatwiejsze do zauważenia.
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).
• Krok 4: Znajdź Q1 i Q3
  Q1 jest medianą (środkiem) dolnej połowy danych, a Q3 jest medianą (środkiem) górnej połowy danych.
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 i Q3 = 16.
• Krok 5: Odejmij Q1 od Q3.
  16 – 7 = 9.
  To jest twój IQR.

Back to Top

Znajdź przedział międzykwartylowy dla nieparzystego zestawu liczb: Alternatywna metoda

Jak być może już wiesz, nic nie jest „ustalone w kamieniu” w statystyce: kiedy niektórzy statystycy znajdują przedział międzykwartylowy dla zestawu liczb nieparzystych, włączają medianę do obu kwartyli. Na przykład, w następującym zestawie liczb: 1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27 niektórzy statystycy podzieliliby go na dwie połowy, włączając medianę (9) do obu połówek:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Prowadzi to do dwóch połówek z parzystym zestawem liczb, więc możesz wykonać powyższe kroki, aby znaleźć IQR.
Back to Top

Rozstęp międzykwartylowy na wykresie kołowym: Jak go znaleźć

Oglądnij film lub przeczytaj kroki poniżej:

Rozstęp międzykwartylowy na wykresie skrzynkowym: Jak go znaleźć

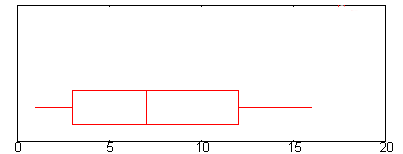
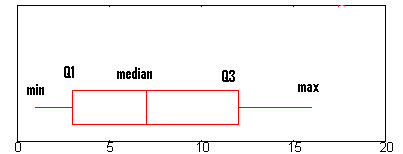
Przykładowe pytanie: Znajdź przedział międzykwartylowy dla powyższego wykresu pudełkowego.

• Krok 1: Znajdź Q1.Q1 jest reprezentowany przez lewą krawędź „pudełka” (w punkcie, w którym zatrzymuje się wisker).
  

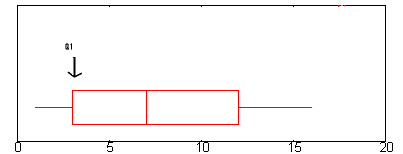
  Na powyższym wykresie Q1 znajduje się w przybliżeniu na poziomie 2,6. (Pełne wyjaśnienie Q1 znajduje się tutaj: Podsumowanie pięciu liczb.)

• Krok 2: Znajdź Q3.
  Q3 jest reprezentowane na wykresie typu boxplot przez prawą krawędź „pudełka”.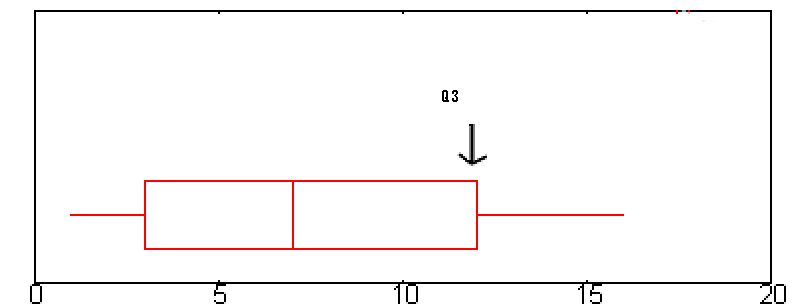
  
  Q3 wynosi około 12 na tym wykresie.
• Krok 3: Odejmij liczbę, którą znalazłeś w kroku 1 od liczby, którą znalazłeś w kroku 3.
  To da Ci przedział międzykwartylowy. 12 – 2,6 = 9,4.

To wszystko!

Back to Top

Interquartile Range in Minitab

Przeczytaj dalej, aby uzyskać wskazówki krok po kroku, lub obejrzyj poniższą wersję wideo.

Przedział kwartyli w programie Minitab: Steps

Przykładowe pytanie: Znajdź w programie Minitab przedział międzykwartylowy dla średniej ocen (GPA) w następującym zbiorze danych:
Grade Point Average (GPA): 1(3,2), 1(3,1), 2(3,5), 2(2,0), 3(1.9), 3(4,0), 3(3,9), 4(3,8), 4(2,9), 5(3,9), 5(3,2), 5(3,3), 6(3,4), 6(2,6), 6(2,5), 7(2,0), 7(1,5), 8(4,0), 8(2,0).

Krok 1: Wpisz dane do arkusza programu Minitab. Wprowadź dane w jednej lub dwóch kolumnach.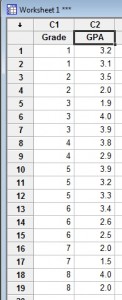

Krok 2: Kliknij przycisk „Stat”, kliknij przycisk „Basic Statistics”, a następnie kliknij polecenie „Display Descriptive Statistics”, aby otworzyć menu Descriptive Statistics.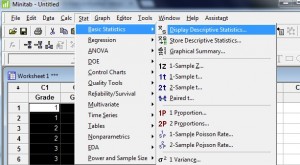

Krok 3: Kliknij nazwę zmiennej w lewym oknie, a następnie kliknij przycisk „Wybierz”, aby przenieść nazwę zmiennej do prawego okna.

Krok 4: Kliknij przycisk „Statystyka”.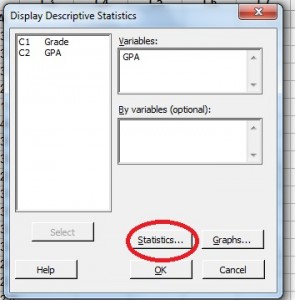

Krok 5: Zaznacz „Interquartile Range.”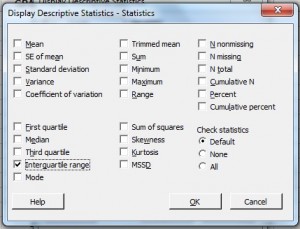
.

Krok 6: Kliknij przycisk „OK” (otworzy się nowe okno z wynikiem). IQR dla GPA w tym konkretnym zestawie danych wynosi 1,8.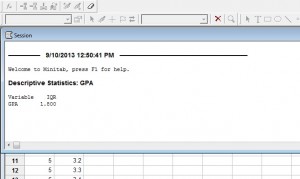

To wszystko!

Wskazówka: Jeśli statystyki opisowe nie są wyświetlane w oknie, kliknij przycisk „Okno” na pasku narzędzi, a następnie kliknij przycisk „Kafelki”. Kliknij okno Sesja (tam pojawiają się statystyki opisowe), a następnie przewiń w górę, aby zobaczyć swoje wyniki.

Back to Top

Jak znaleźć przedział międzykwartylowy Excel 2007

Zobacz film lub przeczytaj poniższe kroki, aby znaleźć przedział międzykwartylowy w programie Excel 2007:

Kroki:
Krok 1: Wprowadź dane do pojedynczej kolumny arkusza Excel. Na przykład wpisz swoje dane w komórkach od A2 do A10. Nie zostawiaj żadnych luk w danych.

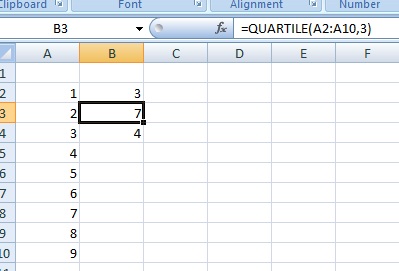
Krok 2: Kliknij pustą komórkę (na przykład komórkę B2), a następnie wpisz =QUARTILE(A2:A10,1). Będziesz musiał zastąpić A2:A10 rzeczywistymi wartościami z twojego zestawu danych. Na przykład, jeśli wpisałeś swoje dane do komórek od B2 do B50, równanie ma postać =QUARTILE(B2:B50,1). Cyfra „1” w formule Excel(A2:A10,1) reprezentuje pierwszy kwartyl (tj. punkt leżący na 25% zestawu danych).

Krok 3: Kliknij drugą pustą komórkę (np. komórkę B3), a następnie wpisz =QUARTILE(A2:A10,3). Zastąp A2:A10 rzeczywistymi wartościami z Twojego zestawu danych. Cyfra „3” w formule Excela (A2:A10,3) reprezentuje trzeci kwartyl (czyli punkt leżący na 75% zestawu danych).

Krok 4: Kliknij trzecią pustą komórkę (na przykład kliknij komórkę B4), a następnie wpisz =B3-B2. Jeśli funkcje kwartyli z kroku 2 i 3 znajdują się w różnych miejscach, zmień odwołania do komórek.

Krok 5: Naciśnij klawisz „Enter”. Excel zwróci IQR w komórce, którą kliknąłeś w kroku 4

To wszystko!

Back to Top

Jak znaleźć przedział międzykwartylowy w SPSS

Jak większość technologii, SPSS ma kilka sposobów na obliczenie IQR. Jednakże, jeśli klikniesz na najbardziej intuicyjny sposób, w jaki spodziewasz się go znaleźć („Statystyki opisowe > Częstości”), niespodzianką jest to, że nie wyświetli on IQR (chociaż wyświetli pierwszy, drugi i trzeci kwartyl). Możesz wybrać tę trasę, a następnie odjąć trzeci kwartyl od pierwszego, aby uzyskać IQR. Jednak najłatwiejszym sposobem znalezienia przedziału międzykwartylowego w SPSS jest użycie polecenia „Eksploruj”. Jeśli masz już wpisane dane do arkusza, przejdź do kroku 3.

Obejrzyj film lub przeczytaj kroki poniżej:

Kroki

Krok 1: Otwórz nowy plik danych w SPSS. Kliknij „Plik”, najedź myszką na „Nowy”, a następnie kliknij „Dane.”

Krok 2: Wpisz swoje dane do kolumn w arkuszu. Możesz użyć tylu kolumn, ile potrzebujesz, ale nie zostawiaj pustych wierszy ani spacji pomiędzy danymi. Zobacz: How to Enter Data into SPSS.

Krok 3: Kliknij „Analyze,” następnie najedź myszką na „Descriptive Statistics.” Kliknij „Eksploruj”, aby otworzyć okno dialogowe „Eksploruj”.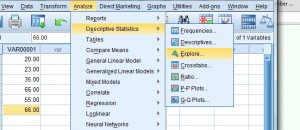

Krok 4: Kliknij nazwę zmiennej (to tylko fantazyjna nazwa nagłówka kolumny), a następnie kliknij górną strzałkę, aby przenieść zmienną do pola „Lista zmiennych zależnych”.

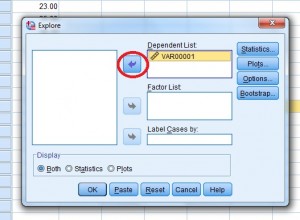
Okno dialogowe „Eksploruj” zmienne.

Krok 5: Kliknij przycisk „OK”. Rozstęp międzykwartylowy jest wymieniony w polu Descriptives.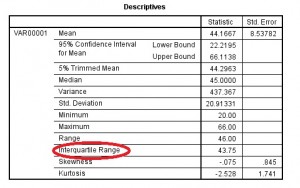

Wskazówka: Ten przykład ma tylko jedną listę wpisaną do arkusza danych, ale możesz mieć kilka do wyboru w zależności od sposobu wprowadzania danych. Upewnij się, że wybrałeś właściwą zmienną (nazwy kolumn) zanim przejdziesz dalej. Jeśli chcesz, aby nazwy zmiennych były bardziej zapadające w pamięć, zmień tytuł kolumny, klikając przycisk „widok zmiennej” znajdujący się na samym dole po lewej stronie arkusza. Wpisz nową nazwę zmiennej, a następnie wróć do widoku danych, klikając przycisk „widok danych”.
Back to Top

Co to jest przedział międzykwartylowy?

Wyobraź sobie wszystkie dane w zbiorze jako punkty na linii liczbowej. Na przykład, jeśli w zbiorze danych znajdują się 3, 7 i 28, wyobraź sobie je jako punkty na linii liczbowej, która jest wyśrodkowana na 0, ale rozciąga się zarówno nieskończenie poniżej, jak i powyżej zera. Po naniesieniu na tę linię liczbową, najmniejszy punkt danych i największy punkt danych w zbiorze danych tworzą granice (tj. dolną i górną granicę) przedziału przestrzeni na linii liczbowej, który zawiera wszystkie punkty danych w zbiorze. Rozstęp międzykwartylowy (IQR) to długość środkowych 50% tego przedziału przestrzeni.

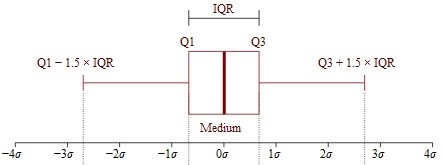
Rozstęp międzykwartylowy to środkowe 50% zbioru danych. Box and whiskers image by Jhguch at en.wikipedia

Jeśli chcesz wiedzieć, że IQR jest w kategoriach formalnych, IQR oblicza się jako: Różnica między trzecim lub górnym kwartylem a pierwszym lub dolnym kwartylem. Kwartyl jest terminem używanym do opisania sposobu podziału zestawu danych na cztery równe porcje (pomyśl o ćwiartce).

Przykład IQR

Jeśli masz zbiór zawierający punkty danych 1, 3, 5, 7, 8, 10, 11 i 13, pierwszy kwartyl to 4, drugi to 7.5, a trzeci to 10.5. Narysuj te punkty na linii liczbowej, a zobaczysz, że te trzy liczby dzielą linię liczbową na ćwiartki od 1 do 13. W związku z tym IQR dla tego zestawu danych wynosi 6,5, obliczone jako 10,5 minus 4. Pierwszy i trzeci kwartyl są również czasami nazywane 25. i 75. percentylem, ponieważ są to równoważne liczby, gdy zbiór danych jest podzielony na procenty, a nie na ćwiartki.

Back to Top

Zakres międzykwartylowy przy użyciu TI83

Obejrzyj wideo lub przeczytaj kroki poniżej:

Możesz użyć kalkulatora przedziału międzykwartylowego online na tej stronie, ale może to nie być możliwe w quizie lub teście. Większość instruktorów pozwala na używanie TI-83 na testach, a nawet jest to jeden z niewielu kalkulatorów dozwolonych na egzaminie AP Statistics. Znalezienie przedziału międzykwartylowego TI 83 nie wymaga niczego więcej niż wprowadzenia listy danych i naciśnięcia kilku przycisków.

Przykładowy problem: Znajdź przedział międzykwartylowy TI 83 dla wysokości 10 najlepszych budynków na świecie (stan na 2009 rok). Wysokości, (w stopach) to: 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272.

Kroki

Krok 1: Wprowadź powyższe dane do listy na kalkulatorze TI 83. Naciśnij przycisk STAT, a następnie naciśnij klawisz ENTER. Wprowadź pierwszą liczbę (2717), a następnie naciśnij ENTER. Kontynuuj wprowadzanie liczb, naciskając ENTER po każdym wpisie.

Krok 2: Naciśnij przycisk STAT.

Krok 3: Naciśnij przycisk strzałki w prawo (przyciski strzałek znajdują się w prawym górnym rogu klawiatury), aby wybrać „Calc.”

Krok 4: Naciśnij ENTER, aby podświetlić „1-Var Stats.”

Krok 5: Naciśnij ENTER ponownie, aby wyświetlić listę statystyk.

Krok 6:Przewiń listę za pomocą klawiszy strzałek, aby znaleźć Q1 i Q3. Zapisz te numery. Mógłbyś skopiować i wkleić te liczby, ale niestety Texas Instruments nie ułatwia tego:

1. Użyj klawiszy strzałek, aby umieścić kursor na początku tekstu, który chcesz podświetlić.
2. Na klawiaturze TI naciśnij i przytrzymaj klawisz Shift, a następnie użyj klawiszy strzałek, aby podświetlić tekst.
3. Zwolnij klawisz Shift i klawisz strzałek.

Menu kopiowania i wklejania powinno się pojawić, umożliwiając skopiowanie i wklejenie danych. Musiałbyś to robić dwa razy (za każdym razem wracając do ekranu HOME), więc znacznie szybciej jest po prostu zapisać liczby.

Krok 7:Odejmij Q1 od Q3, aby znaleźć IQR (strong>624 stopy dla tego zestawu liczb).

To wszystko!
Back to Top

How to Find Q1, Q3 and the Interquartile Range TI 89

Zobacz film lub przeczytaj kroki poniżej:

Przykładowy problem: Znajdź Q1, Q3, oraz IQR dla następującej listy liczb: 1, 9, 2, 3, 7, 8, 9, 2.

Krok 1: Naciśnij APPS. Przewiń do Stats/List Editor (użyj klawiszy strzałek na klawiaturze, aby przewinąć). Naciśnij ENTER. Jeśli nie masz edytora statystyk/list możesz go ściągnąć tutaj.

Krok 2: Wyczyść edytor list z danych: naciśnij F1 8.

Krok 3: Naciśnij ALPHA 9 ALPHA 1 ENTER. W ten sposób nazwiesz swoją listę „IQ.”

Krok 4: Wprowadź swoje numery, jeden po drugim. Po każdym wpisie naciśnij klawisz ENTER. Dla naszej grupy liczb wpisz
1,9,2,3,7,8,9,2

Krok 5: Wciśnij F4, a następnie ENTER (aby wyświetlić ekran statystyk 1-warstwowych).

Krok 6: Powiedz kalkulatorowi, że chcesz statystyki dla listy o nazwie „IQ”, wpisując ALPHA 9 ALPHA 1 w polu „Lista:”. Kalkulator powinien automatycznie ustawić kursor w tym miejscu. Naciśnij ENTER dwa razy.

Krok 7:Przeczytaj wyniki. Q1 jest zapisane jako Q1X (w naszym przykładzie Q1X=2). Q3 jest zapisane jako Q3X (Q3X=8,5). Aby znaleźć IQR, odejmij Q1 od Q3 na ekranie głównym. IQR wynosi 8,5-2=6,5.

To wszystko!

Back to Top

Czym jest Formuła Rozstępu Międzykwartylowego?

Sformułowanie IQR to:
IQR = Q3 – Q1

Gdzie Q3 jest górnym kwartylem, a Q1 dolnym kwartylem.

IQR jako test na rozkład normalny

Użyj wzoru na zakres międzykwartylowy wraz ze średnią i odchyleniem standardowym, aby sprawdzić, czy populacja ma rozkład normalny. Wzory pozwalające określić, czy populacja ma rozkład normalny, czy nie, są następujące:
Q1 – (σ z1) + X
Q3 – (σ z3) + X
Gdzie Q1 to pierwszy kwartyl, Q3 to trzeci kwartyl, σ to odchylenie standardowe, z to wynik standardowy („z-score”), a X to średnia. Aby stwierdzić, czy populacja ma rozkład normalny, należy rozwiązać oba równania, a następnie porównać wyniki. Jeśli istnieje znacząca różnica między wynikami a pierwszym lub trzecim kwartylem, to populacja nie jest normalnie rozłożona.

Back to Top

Do czego służy przedział międzykwartylowy?

IQR służy do pomiaru, jak bardzo punkty danych w zbiorze są oddalone od średniej zbioru danych. Im wyższy IQR, tym bardziej rozłożone są punkty danych; dla kontrastu, im mniejszy IQR, tym bardziej skupione są punkty danych wokół średniej. Zakres IQR jest jedną z wielu miar używanych do pomiaru rozproszenia punktów danych w zbiorze danych. Najlepiej używać go wraz z innymi miarami, takimi jak mediana i całkowity zakres, aby zbudować pełny obraz tendencji zbioru danych do skupiania się wokół swojej średniej.
Back to Top

Skąd pochodzi termin „Rozstęp Międzykwartylowy”?

Kto wymyślił termin „Rozstęp Międzykwartylowy”? Aby się tego dowiedzieć, musimy cofnąć się do XIX wieku.

Historia

Brytyjski lekarz Sir Donald MacAlister użył terminów lower quartile i higher quartile w publikacji z 1879 roku, The Law of the Geometric Mean. Proc. R. Soc. XXIX, s. 374: „”Ponieważ te dwie miary, wraz ze średnią, dzielą krzywą obiektu na cztery równe części, proponuję nazwać je odpowiednio 'wyższym kwartylem' i 'niższym kwartylem'.”

Pomimo że z zawodu był lekarzem, był uzdolniony matematycznie i osiągnął najwyższy wynik w końcowych egzaminach z matematyki na Uniwersytecie Cambridge w 1877 roku. Znał dziewiętnaście języków, w tym angielski, czeski i szwedzki.

Praca Macalistera, Prawo średniej geometrycznej, była właściwie odpowiedzią na pytanie Francisa Galtona (wynalazcy tablicy Galtona). Jednak dopiero w 1882 roku Galton („Report of the Anthropometric Committee”) użył wartości górnego i dolnego kwartyla oraz terminu „interquartile range” – zdefiniowanego jako dwukrotność błędu prawdopodobnego. Galton był nie tylko statystykiem – był także antropologiem, geografem, proto-geneteistą i psychometrykiem, który wydał ponad 340 książek. Ukuł również terminy statystyczne „korelacja” i „regresja w kierunku średniej”

Gonick, L. i Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, s. 20-21, 1993.

—————————————————————————–

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązanie swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!