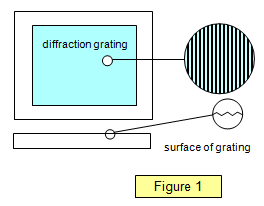
Jeśli liczba szczelin w przeszkodzie jest duża, poprawia się ostrość wzoru, maksima stają się węższe. Przeszkody z dużą liczbą szczelin (więcej niż, powiedzmy, 20 na milimetr) są nazywane siatkami dyfrakcyjnymi. Zostały one po raz pierwszy opracowane przez Fraunhofera pod koniec XVIII wieku i składały się z cienkiego srebrnego drutu nawiniętego na dwie równoległe śruby, co dawało około 30 przeszkód na milimetr. d tego czasu wprowadzono wiele ulepszeń, w 1882 roku Rowland użył diamentu do wyznaczania cienkich linii na szkle, grzbiety działały jak szczeliny, a linijki jak przeszkody (patrz rysunek 1). Używając tej metody możliwe jest uzyskanie siatek dyfrakcyjnych z 3000 linii na milimetr, chociaż „grube” siatki z około 500 liniami na milimetr są lepsze do ogólnego użytku.
W wielu szkołach dwa typy są w powszechnym użyciu, jeden z 300 liniami na mm, a drugi z 80 liniami na mm.
Siatki odbiciowe są również używane, gdzie obraz rozproszony jest oglądany po odbiciu od orzeczonej powierzchni. Bardzo dobrym przykładem siatki dyfrakcyjnej odbiciowej jest płyta CD. Płyta DVD z drobniejszymi liniami daje znacznie szerszy wzór dyfrakcyjny.
Teoria fal i siatka dyfrakcyjna
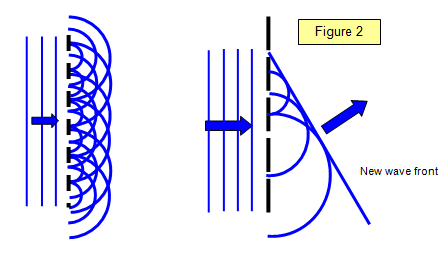
Rysunek 2 pokazuje konstrukcję Huygensa dla siatki. Widać jak okrągłe fale rozproszone z każdej szczeliny sumują się w pewnych kierunkach dając falę rozproszoną, która ma płaski czoło tak jak fale uderzające w kratę od lewej strony. Ta płaska fala powstaje przez narysowanie linii, która spotyka wszystkie małe okrągłe fale i jest nazywana obwiednią wszystkich tych małych fal wtórnych.
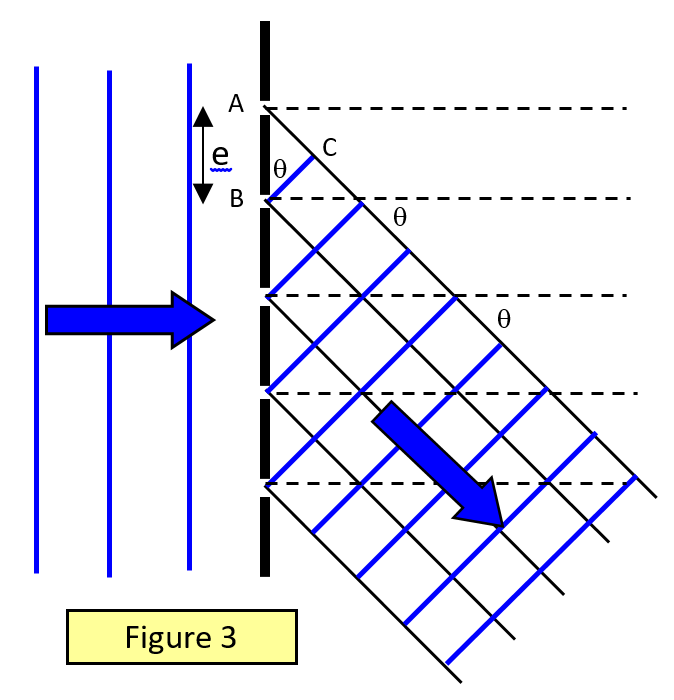
Wzór na siatkę dyfrakcyjną
Rozważmy równoległą wiązkę światła padającą normalnie na siatkę dyfrakcyjną o odstępie między liniami e (odstęp między liniami jest odwrotnością liczby linii na jednostkę długości). Rozważmy światło, które ulega dyfrakcji pod kątem q do normalnej i pochodzi z odpowiednich punktów na sąsiednich szczelinach (Rysunek 3).
Dla maksimum różnica dróg = AC = mλ
Ale AC = e sinθ. Dlatego dla maksimum:
mλ = e sinθ
gdzie m = 0, 1, 2,3….
Liczba m jest znana jako rząd widma, to znaczy, że widmo pierwszego rzędu powstaje dla m = 1, i tak dalej.
Jeśli używane jest światło o pojedynczej długości fali, takie jak z lasera, wtedy pojawia się seria ostrych linii, po jednej linii na każdy rząd widma. W przypadku źródła światła białego powstaje seria widm, przy czym światło o najkrótszej długości fali ma najmniejszy kąt dyfrakcji.
W wyprowadzeniu powyższego wzoru założyliśmy, że padająca wiązka jest pod kątem prostym do powierzchni kraty. Jeżeli tak nie jest, należy uwzględnić ten fakt. Najprostszym sposobem jest zmierzenie pozycji widma pierwszego rzędu po obu stronach środka, zapisanie kąta pomiędzy tymi pozycjami, a następnie zmniejszenie go o połowę, jak pokazano na rysunku 4.
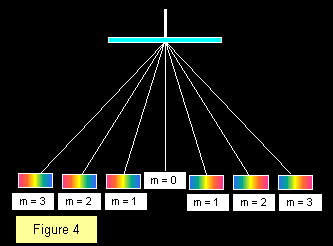
Liczba rzędów widm widocznych z daną kratą zależy od odstępu między kratami, więcej widm jest widocznych z grubszymi kratami. Obiegowa strona kraty powinna być zawsze skierowana w kierunku przeciwnym do padającego światła, aby uniknąć błędów spowodowanych zmianą kierunku z powodu załamania światła w szkle. Schemat przedstawia centralną białą falę z trzema widmami po obu stronach, co daje w sumie siedem obrazów.
(Zob. przykładowy problem)
1. Oblicz długość fali światła monochromatycznego, w którym obraz drugiego rzędu ulega dyfrakcji pod kątem 25o przy użyciu siatki dyfrakcyjnej o 300 liniach na milimetr.
Odstępy między siatkami (e) = 10-3/300 m = 3.3×10-6 m
Długość fali (l) = esin25/2 = /2 = 6.97×10-7 m = 697 nm
2. Oblicz maksymalną liczbę rzędów widocznych przy użyciu siatki dyfrakcyjnej o 500 liniach na milimetr, stosując światło o długości fali 600 nm.
Maksymalny kąt dyfrakcji = 90o e = 10-3/500 = 2×10-6 m
Więc m = esinq/l = 2×10-6/600×10-9 = 3,33
Więc maksymalna liczba rzędów = 3, a w sumie można zobaczyć siedem obrazów źródła (po trzy z każdej strony obrazu centralnego).
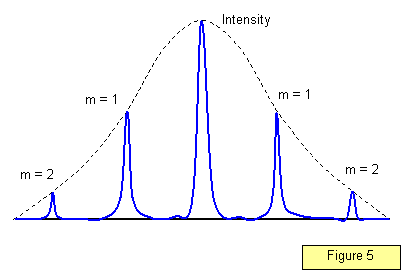
Rozkład natężenia we wzorze dyfrakcyjnym dla dużej liczby szczelin pokazany jest na rysunku 5. Zauważ, że maksima stają się znacznie ostrzejsze; im większa liczba szczelin na metr, tym lepiej zdefiniowane są maksima.
Dyfrakcja światła kadmu lub rtęci jest wykorzystywana do wyznaczania separacji dwóch linii na układzie scalonym. Otrzymano następujące wyniki dla obrazów dyfrakcyjnych drugiego rzędu dla różnych długości fali. Wykorzystaj je do wykreślenia odpowiedniego wykresu liniowego, a następnie wyznacz średnią odległość między przewodami na obwodzie.
| Długość fali/nm | Kąt dyfrakcji (o) |
| 468 | 28.0 |
| 480 | 28.7 |
| 509 | 31.0 |
| 546 | 33.0 |
| 577 | 35.5 |
| 644 | 40.0 |