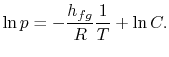Next: 8.5 Rankine Power Cycles Up: 8. Power Cycles with Previous: 8.3 The Carnot Cycle Contents Index
até agora só consideramos os gases ideais e gostaríamos de saber como as propriedades 
, etc. são verdadeiras variáveis de estado e que a 1ª e 2ª leis da termodinâmica se mantêm quando o workingmedium não é um gás ideal (ou seja, um meio de duas fases). Uma forma elegante de o fazer é considerar um ciclo Carnot para um meio bifásico. Afirmar o facto de que todos os motores Carnot operados entre duas temperaturas dadas têm a mesma eficiência é uma forma de afirmar a 2ª lei da termodinâmica. O fluido de trabalho não precisa de ser um gás ideal e pode ser um meio com duas fases de mudança.
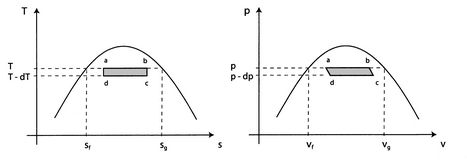
p> A ideia é fazer funcionar um motor Carnot entre temperaturas 
e
para um meio bifásico e deixá-lo passar por uma mudança de fase. Podemos então derivar uma importante relação conhecida como a equação deClausius-Clapeyron, que dá a inclinação da curva de pressão do vapor. Poderíamos então medir a curva de pressão de vapor para várias substâncias e comparar a inclinação medida com a equação deClausius-Clapeyron. Isto pode então ser visto como prova anexperimental da validade geral da 1ª e 2ª leis da termodinâmica!div>
caption> Figura 8.8:Ciclo de Carnot concebido para testar a validade das leis da termodinâmicaítulo>>br>
/div>>br>>>/div>>p>considerar o ciclo infinitesimal de Carnot 
mostrado emFigure 8.8. O calor é absorvido entre estados
e 
. Para vaporizar uma quantidade arbitrária de massa, 
, a quantidade de calor
 |
(8..1) |
m must be supplied to the system. Da 1ª e 2ª leis da termodinâmica a eficiência térmica para um ciclo de Carnot pode ser escrita como
 |
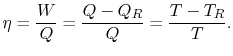Hence, para o ciclo infinitesimal considerado acima,
 |
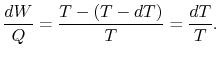(8..2) |
>br> O trabalho ao longo 
e 
quase cancelar de tal forma que o trabalho em rede seja a diferença entre o trabalho ao longo de 
e 
, e 
pode ser vista como a área delimitada pelo rectângulo :
 |
|
| (8..3) |
>br>Substituting Equations (8.1) e(8.3) em (8.2) oneobtains
 |
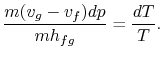br>Termos de rearranjo produzem o Clausius-Equação de Clapeyron,que define o declive da curva de pressão do vapor:
 |
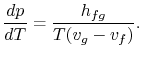(8…4) |
A beleza é que encontrámos uma relação geral entre quantidades experimentalmente mensuráveis dos primeiros princípios (1ª e 2ª leis da termodinâmica).
Para traçar a relação Clausius-Clapeyron e compará-la com as curvas de pressão de vapor medidas experimentalmente, precisamos de integrar a Equação (8.4). Para tal, o aquecimento da vaporização e os volumes específicos têm de ser conhecidos da temperatura. Este é um problema importante em físico-química, mas não o prosseguiremos aqui, excepto para mencionar que se
- variações no calor de vaporização podem ser negligenciadas,
- a fase de vapor é assumida como sendo um gás ideal, e
- o volume específico do líquido é pequeno em comparação com o da fase de vapor,
 |
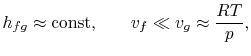a integração pode ser prontamente realizada8.1. Fazendo estas aproximações, o Clausius…Clapeyronequation torna-se
 |
levando a cabo a integração, a expressão resultante é
Nota que as curvas de pressão de vapor são linhas rectas se 
isplotted versus 
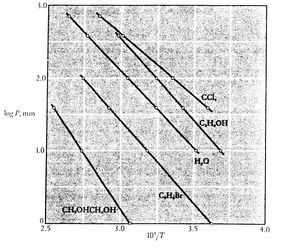
e que a inclinação das curvas é
, directamente relacionados com o calor da vaporização.As figuras 8.9, 8.9 e 8.22 mostram as curvas de pressão de vapor para substâncias variadas. O facto de todas as substâncias conhecidas na região de duas fases cumprirem a equação de Clausius-Clapeyron, proporciona a validade geral da 1ª e 2ª leis da termodinâmica! igura 8.9:Prova Experimental de Clausius-Clapeyron(1) ítulo>>br>>>div>
>br>>>/div>>>div>>>>br>>capítulo> Figura 8.10:Clausius-Clapeyron Experimental Proof(2) >br>
br>>>/div>
Next: 8.5 Rankine Power Cycles Up: 8. Power Cycles with Previous: 8.3 The Carnot Cycle Contents Index
UnifiedTP