Heading

O que é uma Interquartil Range?

A Interquartil Range é uma medida de onde os “cinquenta médios” se encontram num conjunto de dados. Onde um intervalo é uma medida de onde o início e o fim estão num conjunto, um intervalo interquartílico é uma medida de onde se encontra a maior parte dos valores. É por isso que é preferida em relação a muitas outras medidas de dispersão ao relatar coisas como o desempenho escolar ou pontuações SAT.

A fórmula do intervalo interquartil é o primeiro quartil subtraído do terceiro quartil:

Conteúdo (clique para saltar para a secção da página):

Solving by hand:
/p>

1. Solve a fórmula à mão (conjunto ímpar de números).
2. E se eu tiver um conjunto par de números?
3. Encontrar um intervalo interquartil para um conjunto ímpar de números: Segundo Método
4. Box Plot Interquartil de intervalo interquartil: Como encontrá-lo

Utilizar Tecnologia:

1. Gama interquartílico no Minitab
2. Gama interquartílico no Excel
3. Gama interquartílico no SPSS
4. Gama interquartílico na TI83
5. Q1, Q3 e o IQR na TI89

Informação geral:

1. O que é um intervalo interquartílico?
2. Qual é a Fórmula da Gama Interquartil?
3. IQR como Teste para Distribuição Normal
4. Para que é usada uma Gama Interquartil?
5. História da Gama Interquartil.

Solva a fórmula à mão.

Veja o vídeo ou leia os passos abaixo. Se ainda tiver dificuldades, verifique os tutores em Chegg.com. Os seus primeiros 30 minutos são gratuitos!

h2>Passos:

• Passo 1: Ponha os números em ordem.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.
• Passo 2: Encontrar a mediana.
  1, 2, 5, 6, 7, 9, 12, 15, 18, 19, 27.

Passo 3: Colocar parênteses em torno dos números acima e abaixo da mediana.
Não é necessário estatisticamente, mas torna Q1 e Q3 mais fáceis de identificar.
(1, 2, 5, 6, 7), 9, (12, 15, 18, 19, 27).

• Passo 4: Encontrar Q1 e Q3
  Pense em Q1 como uma mediana na metade inferior dos dados e pense em Q3 como uma mediana na metade superior dos dados.
  (1, 2, 5, 6, 7), 9, ( 12, 15, 18, 19, 27). Q1 = 5 e Q3 = 18.
• Passo 5: Subtrair Q1 de Q3 para encontrar o intervalo interquartil.
  18 – 5 = 13.

Tal como a explicação? Veja o Manual de Estatísticas Práticas de Engano, que tem mais centenas de explicações passo-a-passo, tal como esta!

E se eu tiver um Conjunto Par de Números?

P>Pergunta de exemplo: Encontre o IQR para o seguinte conjunto de dados: 3, 5, 7, 8, 9, 11, 15, 16, 20, 21.

• Passo 1: Ponha os números em ordem.
  3, 5, 7, 8, 9, 11, 15, 16, 20, 21.

Passo 2: Faça uma marca no centro dos dados:
3, 5, 7, 8, 9, | 11, 15, 16, 20, 21.

• Passo 3: Colocar parênteses em torno dos números acima e abaixo da marca que fez no Passo 2 faz com que Q1 e Q3 sejam mais fáceis de identificar.
  (3, 5, 7, 8, 9), | (11, 15, 16, 20, 21).

li> Passo 4: Encontrar Q1 e Q3
Q1 é a mediana (o meio) da metade inferior dos dados, e Q3 é a mediana (o meio) da metade superior dos dados.
(3, 5, 7, 8, 9), | (11, 15, 16, 20, 21). Q1 = 7 e Q3 = 16.

• Passo 5: Subtrair Q1 de Q3.
  16 – 7 = 9.
  Este é o seu IQR.

Back to Top

Encontrar um intervalo interquartil para um conjunto ímpar de números: Método alternativo

Como já deve saber, nada é “definido em pedra” nas estatísticas: quando alguns estatísticos encontram um intervalo interquartílico para um conjunto de números ímpares, incluem a mediana em ambos os quartis. Por exemplo, no conjunto de números que se segue: 1, 2, 5, 6, 7, 9, 9, 12, 15, 18, 19, 27 alguns estatísticos dividiriam-no em duas metades, incluindo a mediana (9) em ambas as metades:
(1, 2, 5, 6, 7, 9), (9, 12, 15, 18, 19, 27)
Isto leva a duas metades com um conjunto par de números, pelo que se pode seguir os passos acima para encontrar o IQR.
Voltar para o topo

Box Plot Interquartil: Como encontrá-lo

Veja o vídeo ou leia os passos abaixo:

div>Por favor aceite estatísticas, comercializando cookies para ver este vídeo.

Box Plot Interquartil intervalo interquartil: Como encontrá-lo

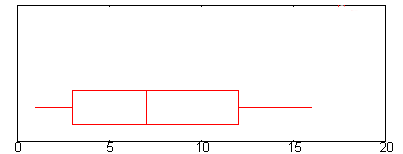
P>Pergunta de amostra: Encontrar o intervalo interquartil para o gráfico da caixa acima.

• Passo 1: Encontrar Q1.Q1 é representado pela extremidade esquerda da “caixa” (no ponto onde o bigode pára).
  

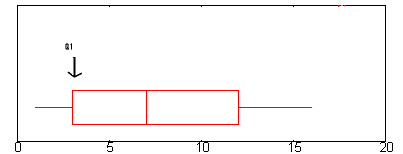
  No gráfico acima, Q1 está aproximadamente em 2.6. (Uma explicação completa de Q1 está aqui: O resumo dos cinco números.)

• Passo 2: Encontrar Q3.
  Q3 é representado numa boxplot pela margem direita da “caixa”.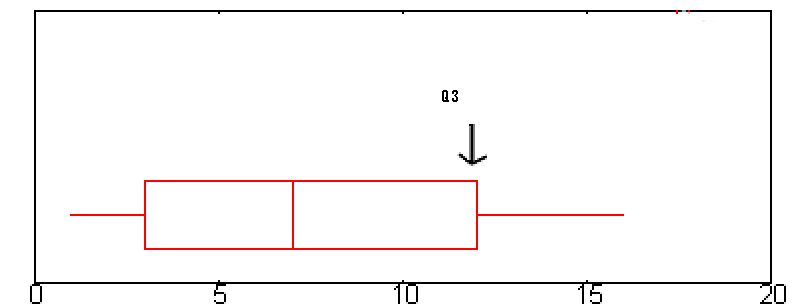
  br>br>Q3 é aproximadamente 12 neste gráfico.
• Passo 3: Subtraia o número que encontrou no passo 1 ao número que encontrou no passo 3.
  Isto dar-lhe-á o intervalo interquartílico. 12 – 2.6 = 9.4.

É isso!

Voltar para o topo

Gama interquartil no Minitab

br>>Leia para instruções passo a passo, ou veja a versão vídeo abaixo.

Gama Interquartílica no Minitab: Passos

P>Pergunta de amostra: Encontre um intervalo interquartílico no Minitab para a Média de Pontos de Classificação (GPA) no seguinte conjunto de dados:
Média de Pontos de Classificação (GPA): 1(3.2), 1(3.1), 2(3.5), 2(2.0), 3(1).9), 3(4.0), 3(3.9), 4(3.8), 4(2.9), 5(3.9), 5(3.2), 5(3.3), 5(3.3), 6(3.4), 6(2.6), 6(2.5), 7(2.0), 7(1.5), 8(4.0), 8(2.0).

Passo 1: Digite os seus dados numa folha de trabalho do Minitab. Introduza os seus dados em uma ou duas colunas.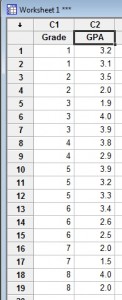

passo 2: Clique em “Stat,” depois clique em “Basic Statistics,” depois clique em “Display Descriptive Statistics,” para abrir o menu Descriptive Statistics.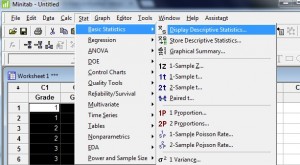

P>Passo 3: Clique num nome de variável na janela da esquerda e depois clique no botão “Seleccionar” para transferir o nome da variável para a janela da direita.

P>Passo 4: Clique no botão “Statistics”.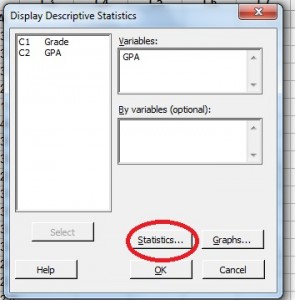

P>Passo 5: Marque “Interquartile Range”.”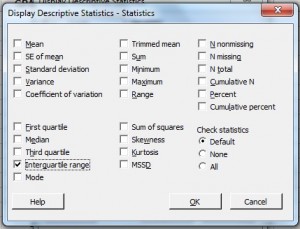
.

passo 6: Clique no botão “OK” (abrirá uma nova janela com o resultado). O IQR para o GPA neste conjunto de dados em particular é 1.8.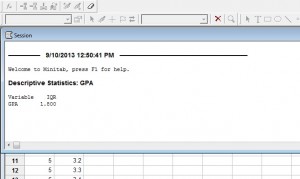

p>É isso!

Tip: Se não vê estatísticas descritivas mostradas numa janela, clique em “Window” na barra de ferramentas, depois clique em “Tile”. Clique na janela Sessão (é aqui que aparece a estatística descritiva) e depois role para cima para ver os seus resultados.

p>Voltar ao Topo

Como encontrar um intervalo interquartílico no Excel 2007

Veja o vídeo ou leia os passos abaixo para encontrar um intervalo interquartílico no Excel 2007:

br>Passos:
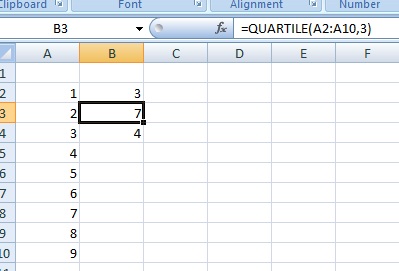
Passo 1: Introduza os seus dados numa única coluna do Excel numa folha de trabalho. Por exemplo, digite os seus dados nas células A2 a A10. Não deixe lacunas nos seus dados.

passo 2: Clique numa célula em branco (por exemplo, clique na célula B2) e depois digite =QUARTILE(A2:A10,1). Terá de substituir A2:A10 pelos valores reais do seu conjunto de dados. Por exemplo, se digitou os seus dados em B2 a B50, a equação é =QUARTILE(B2:B50,1). O “1” nesta fórmula Excel(A2:A10,1) representa o primeiro quartil (isto é, o ponto situado a 25% do conjunto de dados).

P>Passo 3: Clique numa segunda célula em branco (por exemplo, clique na célula B3) e depois digite =QUARTILE(A2:A10,3). Substitua A2:A10 pelos valores reais do seu conjunto de dados. O “3” nesta fórmula Excel (A2:A10,3) representa o terceiro quartil (ou seja, o ponto situado a 75% do conjunto de dados).

Passo 4: Clicar numa terceira célula em branco (por exemplo, clicar na célula B4) e depois digitar =B3-B2. Se as suas funções de quartil do Passo 2 e 3 estiverem em locais diferentes, altere as referências das células.

P>Passo 5: Prima a tecla “Enter”. O Excel devolverá o IQR na célula em que clicou no Passo 4

É isso!

Voltar ao Topo

Como encontrar um intervalo interquartil no SPSS

Como a maioria da tecnologia, o SPSS tem várias formas de calcular o IQR. No entanto, se clicar na forma mais intuitiva que esperaria encontrar (“Descriptive Statistics > Frequencies”), a surpresa é que não irá listar o IQR (embora irá listar o primeiro, segundo e terceiro quartis). Poderia tomar esta rota e depois subtrair o terceiro quartil do primeiro para obter o IQR. No entanto, a forma mais fácil de encontrar o intervalo interquartil no SPSS é utilizando o comando “Explorar”. Se já tiver digitado dados na sua folha de trabalho, salte para o Passo 3.

Veja o vídeo ou leia os passos abaixo:

Passos

Passo 1: Abra um novo ficheiro de dados no SPSS. Clique em “Ficheiro”, passe o rato sobre “Novo” e depois clique em “Dados”

Passo 2: Digite os seus dados em colunas na folha de trabalho. Pode usar tantas colunas quantas precisar, mas não deixe linhas ou espaços em branco entre os seus dados. Veja: Como introduzir dados em SPSS.

P>Passo 3: Clique em “Analisar”, depois passe o rato sobre “Estatística Descritiva”. Clique em “Explore” para abrir a caixa de diálogo “Explore”.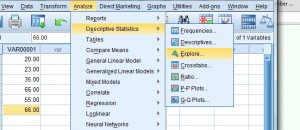

P>Passo 4: Clique no nome da variável (isso é apenas um nome extravagante para o cabeçalho da coluna), depois clique na seta superior para mover a variável para a caixa “Lista Dependente”.

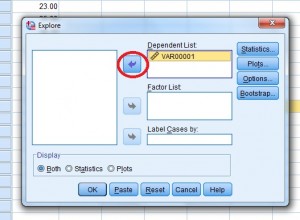
A caixa de diálogo “Explorar” variáveis.

P>Passo 5: Clique em “OK”. O intervalo interquartil está listado na caixa Descritivas.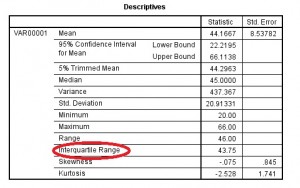

Tip: Este exemplo tem apenas uma lista digitada na folha de dados, mas pode ter várias para escolher, dependendo de como introduziu os seus dados. Certifique-se de seleccionar a variável correcta (nomes de colunas) antes de prosseguir. Se quiser nomes de variáveis mais memoráveis, altere o título da coluna clicando no botão “vista da variável”, no canto inferior esquerdo da folha de trabalho. Escreva o seu novo nome de variável e depois volte à visualização de dados clicando no botão “data view”.
Voltar ao Topo

O que é uma Interquartil Range?

br>Imagine todos os dados de um conjunto como pontos numa linha numérica. Por exemplo, se tiver 3, 7 e 28 no seu conjunto de dados, imagine-os como pontos numa linha numérica centrada em 0, mas que se estende infinitamente abaixo de zero e infinitamente acima de zero. Uma vez traçado nessa linha numérica, o menor ponto de dados e o maior ponto de dados do conjunto de dados criam os limites (ou seja, um limite inferior e um limite superior) de um intervalo de espaço na linha numérica que contém todos os pontos de dados do conjunto. O intervalo interquartil (IQR) é o comprimento dos 50% médios desse intervalo de espaço.

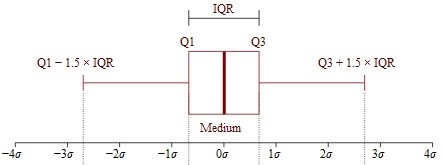
O intervalo interquartil é os 50% médios de um conjunto de dados. Imagem de caixa e bigodes de Jhguch na en.wikipedia

Se quiser saber que o IQR é em termos formais, o IQR é calculado como: A diferença entre o terceiro quartil ou quartil superior e o primeiro quartil ou quartil inferior. Quartil é um termo utilizado para descrever como dividir o conjunto de dados em quatro porções iguais (pensar quarto).

IQR Exemplo

Se tiver um conjunto contendo os pontos de dados 1, 3, 5, 7, 8, 10, 11 e 13, o primeiro quartil é 4, o segundo quartil é 7,5 e o terceiro quartil é 10,5. Desenhe estes pontos numa linha numérica e verá que esses três números dividem a linha numérica nos trimestres de 1 a 13. Como tal, o IQR desse conjunto de dados é 6,5, calculado como 10,5 menos 4. O primeiro e terceiro quartis também são por vezes chamados de percentis 25 e 75 porque esses são os números equivalentes quando o conjunto de dados é dividido em percentagens e não em trimestres.

Back to Top

Interquartil Range usando a TI83

Veja o vídeo ou leia os passos abaixo:

Embora possa usar a calculadora de intervalo interquartil online nifty neste website, isso pode não ser uma opção num questionário ou teste. A maioria dos instrutores permite a utilização de uma TI-83 em testes, e é mesmo uma das poucas calculadoras permitidas no exame AP Statistics. Encontrar o intervalo interquartil TI 83 nada mais envolve do que entrar na sua lista de dados e carregar num par de botões.

Problema de exemplo: Encontre o intervalo interquartil TI 83 para as alturas dos 10 principais edifícios do mundo (a partir de 2009). As alturas, (em pés) são: 2717, 2063, 2001, 1815, 1516, 1503, 1482, 1377, 1312, 1272.

Passos

Passo 1: Introduza os dados acima numa lista na calculadora TI 83. Prima o botão STAT e depois prima ENTER. Introduzir o primeiro número (2717), e depois premir ENTER. Continue a introduzir números, premindo ENTER após cada entrada.

Passo 2: Prima o botão STAT.

Passo 3: Prima o botão de seta para a direita (as teclas de seta encontram-se no canto superior direito do teclado) para seleccionar “Calc.”

P>Passo 4: Prima ENTER para realçar “1-Var Stats”

P>Passo 5: Prima ENTER novamente para trazer uma lista de stats.

Passo 6: Desça a lista com as teclas de setas para encontrar Q1 e Q3. Escreva esses números. Poderia copiar e colar os números mas infelizmente, Texas Instruments não torna isto fácil:

1. Utilizar as teclas de setas para colocar o cursor no início do
   texto que deseja realçar.
2. Utilizar o teclado TI, pressionar e manter pressionada a tecla Shift, e depois utilizar as teclas de setas para realçar o texto.
3. Loquear a tecla Shift e a tecla de setas.

O menu copiar e colar deve aparecer, permitindo-lhe copiar e colar os dados. Teria de fazer isto duas vezes (voltando ao ecrã INÍCIO de cada vez), por isso é muito mais rápido apenas para escrever os números.

P>Passo 7:Subtrair Q1 de Q3 para encontrar o IQR (strong>624 pés para este conjunto de números).

p>É isso!
Voltar ao Topo

Como encontrar Q1, Q3 e o Interquartil TI 89

Veja o vídeo ou leia os passos abaixo:

Problema de amostra: Encontre Q1, Q3, e o IQR para a seguinte lista de números: 1, 9, 2, 3, 7, 8, 9, 2.

Passo 1: Pressione APPS. Desloque-se para Stats/List Editor (use as teclas de setas no teclado para se deslocar). Carregar ENTER. Se não tiver o editor de estatísticas/listas, pode descarregá-lo aqui.

Etapa 2: Limpar o editor de listas de dados: prima F1 8.

Etapa 3: Prima ALPHA 9 ALPHA 1 ENTER. Isto nomeia a sua lista “IQ.”

P>Passo 4: Introduza os seus números, um de cada vez. Siga cada entrada premindo a tecla ENTER. Para o nosso grupo de números, introduza
1,9,2,3,7,8,9,2

Passo 5: Prima F4, depois ENTER (para o ecrã de estatísticas 1-var).

Passo 6: Diga à calculadora que pretende estatísticas para a lista chamada “IQ”, introduzindo ALPHA 9 ALPHA 1 na caixa “Lista:”. A calculadora deve colocar automaticamente o cursor aí para si. Prima ENTER duas vezes.

P>Passo 7:Leia os resultados. Q1 é listado como Q1X (no nosso exemplo, Q1X=2). Q3 é listado como Q3X (Q3X=8,5). Para encontrar o IQR, subtrair Q1 de Q3 no ecrã inicial. O IQR é 8,5-2=6,5,

É isso!

P>Voltar para o topo

O que é a Fórmula do Interquartil?

A fórmula do IQR é:
IQR = Q3 – Q1

Onde Q3 é o quartil superior e Q1 é o quartil inferior.

p>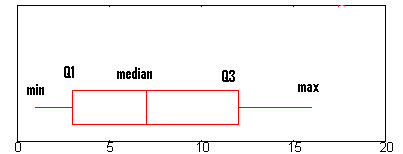

IQR como teste para distribuição normal

br>Utilizar a fórmula do intervalo interquartil com a média e o desvio padrão para testar se uma população tem ou não uma distribuição normal. A fórmula para determinar se uma população tem ou não uma distribuição normal é:
Q1 – (σ z1) + X
Q3 – (σ z3) + X
onde Q1 é o primeiro quartil, Q3 é o terceiro quartil, σ é o desvio padrão, z é a pontuação padrão (“z-score”) e X é a média. Para saber se uma população é normalmente distribuída, resolver ambas as equações e depois comparar os resultados. Se houver uma diferença significativa entre os resultados e o primeiro ou terceiro quartil, então a população não é normalmente distribuída.

Voltar ao Topo

Para que é utilizada uma Interquartil Range For?

br> O IQR é utilizado para medir a distribuição dos pontos de dados num conjunto a partir da média do conjunto de dados. Quanto maior for o IQR, mais espalhados são os pontos de dados; em contraste, quanto menor for o IQR, mais agrupados são os pontos de dados em torno da média. O intervalo IQR é uma das muitas medidas usadas para medir a dispersão dos pontos de dados de um conjunto de dados. É melhor utilizada com outras medições, tais como a mediana e o intervalo total, para construir uma imagem completa da tendência de um conjunto de dados para se agrupar em torno da sua média.
Voltar para o topo

De onde vem o termo Interquartil Range?

Quem inventou o termo “Interquartil Range? Para descobrir isso, temos de voltar ao século XIX.

História

Médico britânico Sir Donald MacAlister utilizou os termos quartil inferior e quartil superior na publicação de 1879, a Lei da Média Geométrica. Proc. R. Soc. XXIX, p. 374: “Como estas duas medidas, com a média, dividem a curva da facilidade em quatro partes iguais, proponho chamar-lhes respectivamente o “quartil superior” e o “quartil inferior””
br>>Al embora um médico por profissão, foi dotado de matemática e alcançou a pontuação mais alta nos exames finais de matemática da Universidade de Cambridge em 1877. Falou dezanove línguas, incluindo inglês, checo e sueco.

p> papel do Macalister, a Lei da Média Geométrica foi na realidade em resposta a uma pergunta apresentada por Francis Galton (inventor do tabuleiro de Galton). Contudo, só em 1882 é que Galton (“Relatório do Comité Antropométrico”) utilizou os valores dos quartis superior e inferior e o termo “intervalo interquartil” – definido como o dobro do erro provável. Galton não era apenas um estatístico – era também um antropólogo, geógrafo, proto-genetista e psicometrista que produziu mais de 340 livros. Ele também cunhou os termos estatísticos “correlação” e “regressão para a média”

Gonick, L. e Smith, W. The Cartoon Guide to Statistics. Nova Iorque: Harper Perennial, pp. 20-21, 1993.

——————————————————————————
p>Need help with a homework or test question? Com o Chegg Study, pode obter soluções passo a passo para as suas perguntas de um especialista na matéria. Os seus primeiros 30 minutos com um tutor do Chegg são gratuitos!