Um algoritmo divide e conquista é uma estratégia de resolução de um grande problema por
- quebrar o problema em sub-problemas menores
- solver os sub-problemas, e
- combiná-los para obter a saída desejada.
Para usar o algoritmo divide e conquista, é utilizada a recursividade. Aprender sobre recorrência em diferentes linguagens de programação:
- Recursão em Java
- Recursão em Python
- Recursão em C++
Como Funcionam os Algoritmos de Dividir e Conquistar?
Aqui estão os passos envolvidos:
- Dividir: Dividir o problema dado em sub-problemas usando recursividade.
- Conquer: Resolver os sub-problemas mais pequenos recursivamente. Se o sub-problema for suficientemente pequeno, então resolva-o directamente.
- Combine: Combine as soluções dos sub-problemas que fazem parte do processo recursivo para resolver o problema real.
Deixe-nos compreender este conceito com a ajuda de um exemplo.
Aqui, vamos ordenar uma matriz utilizando a abordagem dividir e conquistar (ou seja. merge sort).
- Deixe o array dado ser:

Array for merge sort - Dividir o array em duas metades.

Divide o array em duas subpartes br>>b>b>b>b>b>b>b>div, divida cada subparte recursivamente em duas metades até obter elementos individuais.
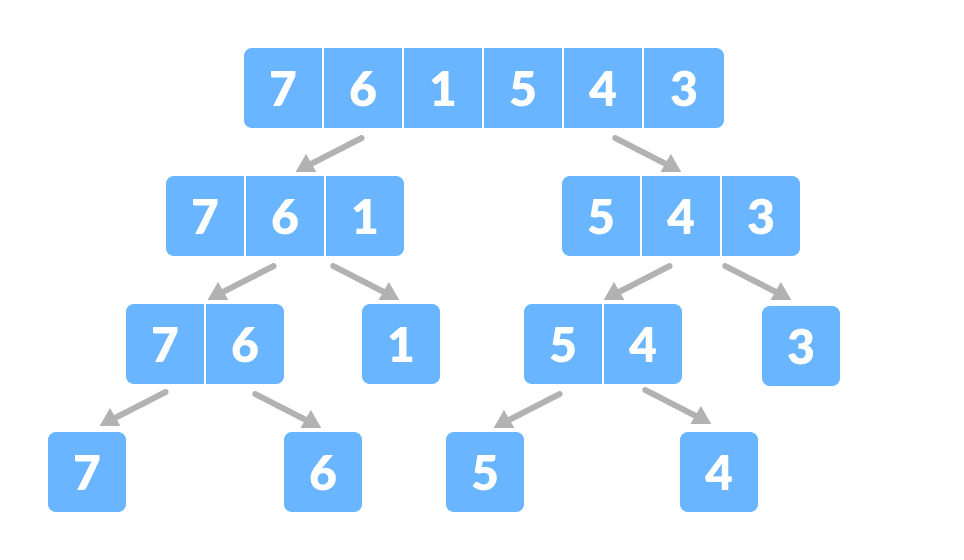
Divida a matriz em subpartes menores - Agora, combine os elementos individuais de uma forma ordenada. Aqui, conquistar e combinar passos vão lado a lado.
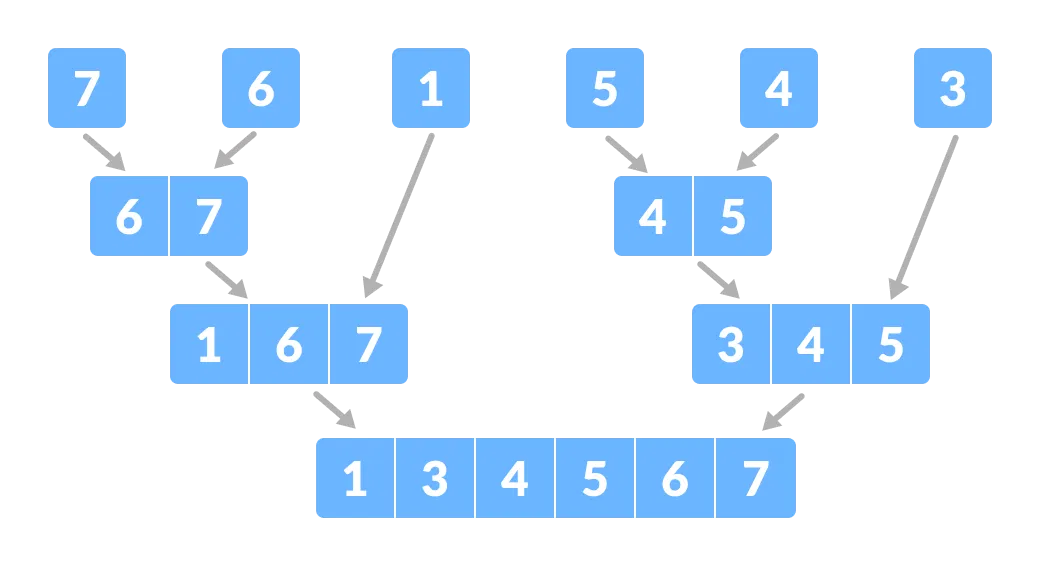
Combinar as subpartes
Complexidade temporal
A complexidade do algoritmo de dividir e conquistar é calculada utilizando o teorema mestre.
T(n) = aT(n/b) + f(n),where,n = size of inputa = number of subproblems in the recursionn/b = size of each subproblem. All subproblems are assumed to have the same size.f(n) = cost of the work done outside the recursive call, which includes the cost of dividing the problem and cost of merging the solutions
Deixe-nos tomar um exemplo para encontrar a complexidade temporal de um problema recursivo.
Para um tipo de fusão, a equação pode ser escrita como:
T(n) = aT(n/b) + f(n) = 2T(n/2) + O(n)Where, a = 2 (each time, a problem is divided into 2 subproblems)n/b = n/2 (size of each sub problem is half of the input)f(n) = time taken to divide the problem and merging the subproblemsT(n/2) = O(n log n) (To understand this, please refer to the master theorem.)Now, T(n) = 2T(n log n) + O(n) ≈ O(n log n)
Abordagem dinâmica de dividir e conquistar Vs
A abordagem dividir e conquistar divide um problema em sub-problemas menores; estes sub-problemas são ainda resolvidos recursivamente. O resultado de cada sub-problema não é armazenado para referência futura, enquanto que, numa abordagem dinâmica, o resultado de cada sub-problema é armazenado para referência futura.
Utilizar a abordagem dividir e conquistar quando o mesmo sub-problema não é resolvido várias vezes. Utilizar a abordagem dinâmica quando o resultado de um subproblema for para ser usado várias vezes no futuro.
Deixe-nos compreender isto com um exemplo. Suponhamos que estamos a tentar encontrar a série Fibonacci. Então,
Abordagem de dividir e conquistar:
fib(n) If n < 2, return 1 Else , return f(n - 1) + f(n -2)
Abordagem dinâmica:
mem = fib(n) If n in mem: return mem else, If n < 2, f = 1 else , f = f(n - 1) + f(n -2) mem = f return f
Numa abordagem dinâmica, mem armazena o resultado de cada sub-capítulo.
Vantagens do Algoritmo Divide and Conquer
- A complexidade para a multiplicação de duas matrizes usando o método ingénuo é O(n3), enquanto que usando a abordagem dividir e conquistar (isto é, a multiplicação da matriz de Strassen) é O(n2.8074). Esta abordagem também simplifica outros problemas, tais como a Torre de Hanói.
li> Esta abordagem é adequada para sistemas de multiprocessamento.li> Faz uso eficiente de caches de memória.
Divide and Conquer Applications
- Binary Search
- Merge Sort
- Quick Sort
- Multiplicação da Matriz de Strassen
- Karatsuba Algorithm



