Construir escadas para o seu deck, pátio ou jardim é uma tarefa incrivelmente difícil.
Antes de colocar as suas ferramentas e começar, precisa de se certificar de que cada degrau será idêntico tanto em tamanho como em forma.
Para o fazer, há muitos parâmetros e medidas que precisa de ter em conta nos seus cálculos.
Mostramos-lhe como isto pode ser feito facilmente. 😉
A nossa calculadora de escadas online pode ajudar a fazer desta tarefa uma brisa.
Simplesmente coloque valores para a corrida e subida totais, juntamente com algumas medidas para os degraus individuais para calcular a disposição da sua escada!
Conteúdo:
Como calcular escadas
Para utilizar a nossa calculadora de escadas, é necessário introduzir, no mínimo, as seguintes medidas:
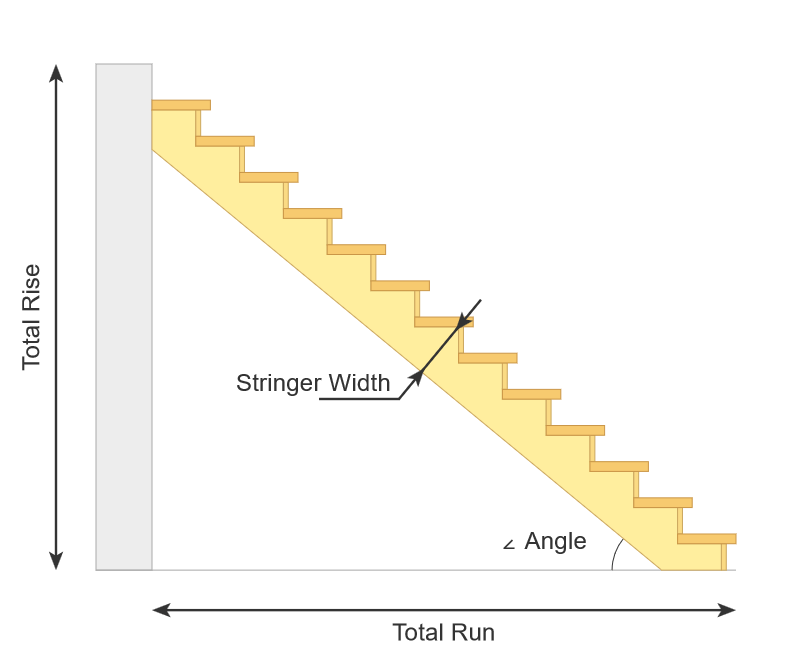
- Total Run – O comprimento horizontal total da stringer
- Total Rise – A altura vertical entre o fundo do primeiro degrau e o topo do degrau final da stringer
- Largura do degrau – A medida total da diagonal entre a borda do degrau e a linha posterior
- Número de degraus necessários
Utilizando estes valores, a nossa calculadora trabalha a elevação vertical de cada passo individual com a fracção:
$Rise = {Total\,Rise Número\,de\,Passos}$$
Além disso, a nossa calculadora permite-lhe escolher entre uma montagem padrão e uma montagem embutida.
A decisão de utilizar uma montagem sobre a outra dependerá da sua situação individual e do seu projecto de bricolage.

Movendo-se através do artigo e explicação, estas fórmulas são bastante abstractas e complicadas.
Para o ajudar a seguir-nos, faremos um exemplo trabalhado.
Isto destina-se aos cálculos, fórmulas e explicações mais fáceis de seguir.
Exemplos de cálculos
- Para ambos os nossos exemplos abaixo, imaginamos que queremos ter 17 degraus a correr até um patamar com uma subida vertical total de 120 polegadas e uma corrida horizontal total de 180 polegadas
- Vamos dizer que temos uma espessura de banda de rodagem de 2 polegadas
- Sobreposição da banda de rodagem de 2 polegadas
- Espessura da banda de rodagem de 1 polegada
- E uma largura da banda de rodagem de 12 polegadas
Leve-nos através dos cálculos do exemplo para primeiro uma montagem padrão, e depois um conjunto de escadas de montagem embutida.
Ao fazê-lo, calcularemos as dimensões dos degraus e da escadaria.
Além disso, mostrar-lhe-emos como a calculadora de strings de escada funciona a subida, corrida, ângulo e comprimento das strings, permitindo-lhe planear eficazmente a disposição da escadaria pretendida.
Seguir estes cálculos, ou simplesmente utilizar a calculadora para fazer o seu projecto de bricolage a uma brisa!
Som bem? 😀
Cálculos de montagem padrão

P>Primeiro, calculamos a elevação vertical de cada degrau:
$Rise = {Total\,Rise Número\,de\,degraus} = {120\,em 17} = 7.06\,in$
Agora, utilizando uma escada de montagem padrão, a subida vertical dos degraus será um degrau a menos do que com uma montagem embutida, porque o degrau final é ocupado pelo terraço. Assim, calculamos:
$$Elevação\,of\,steps = Total\,Elevação – Elevação = 120\,in – 7.06\,in = 112.94\,in$
Agora, se incluirmos a espessura do piso (a espessura do piso em cada degrau), devemos subtrair isto também. A calculadora da escada de plataforma funciona assim:
$$Run\,of\,steps = Total\,Run – (Piso\,Overlap + Riser\,Thickness) = 180\,in – (2\,in + 1\,in) = 177\,in$
Assim, a nossa calculadora da escada de plataforma pode calcular a distância horizontal total entre a borda de cada degrau (não esquecendo que o degrau final é o decking!):
$Run = {Run,of\,of\,steps \,of\,steps} = {177\,in {16} = 11.06\,in$
Agora, se considerarmos um único degrau da escada, a distância horizontal total será dada por:
$Total\,Horizontal\,Distância = Correr + Piso\,Sobreposição + Riser\,Espessura = 11,06\,in + 2\,in + 1\,in = 14,06\,in$
E o ângulo (ou inclinação!) entre a horizontal e a escadaria é calculado por:
$tan\,\alpha_1 = {Subida,de,degraus Corrida,de,degraus} → \alpha_1 = tan^{-1} {Subida,de,degraus {-1} = tan^{-1} {11294,em mais de 177,in = 32,54^o$
Agora, para encontrar o comprimento da corda da escada é necessária alguma Matemática mais complicada. 🧐
P>Cuidado com o exemplo abaixo para o ver em detalhe!
Se considerarmos a stringer, o ângulo entre o degrau esquerdo e o horizontal (α2) é dado subtraindo o ângulo previamente calculado de 90 graus:

$\alpha_2 = 90^o – \alpha_1 = 90^o – 32,54^o = 57.46^o$$
Similiarmente,
$$$=3 = 90^o + \alfa_2 = 90^o + 57,46^o = 147,46^o$$
E
$$$_4 = \alfa_1 = 32,54^o$$
$$\alfa_5 = 90^o + \alfa_1 = 90^o + 32.54^o = 122,54^o$
Além disso, a calculadora é capaz de calcular as dimensões horizontal e vertical do stringer.
Para facilidade de compreensão, mais uma vez, ver a imagem de referência. A calculadora calcula todas estas distâncias usando o método dado abaixo:

$A_1 = Ascensão × pecado\,\alpha_2 = 7.06\,in × sin\,57.46^o = 5.95\,in$$
$A_2 = Stringer\,Width – A_1 = 12\,in – 5.95\,in = 6.05\,in$
$C_2 = \sqrt{Run^2 – {A_1}^2} = \sqrt{(11.06\,in)^2 – (5.95\,in)^2} = 9.32\,in$$
$C_3 = A_1 × tan\,\alpha_2 = 5.95\,in × tan\,57.46^o = 9.33\,in$
$B_1 = \sqrt{Rise^2 – {A_1}^2} = \sqrt{(7.06\,in)^2- (5.95\,in)^2} = 3.8\,in$
$B_2 = A_2 × tan\,\alpha_1 = 6.05\,in × tan\,32.54^o = 3.86\,in$$
$B_3 = (Aumento -Tread\,Espessura) × cos\,\alfa_2 = (7,06\,in – 2\,in) × cos\,57,46^o = 2.72\,in$
$A_3 = (Subida – Piso – Espessura) × cos\,\alfa_1 = (7.06\,in – 2\,in) × cos\,32.54^o = 4.26\,in$
$A_4 = Stringer\,Width – A_3 = 12\,in – 4.27\,in = 7,74\,in$
$C_4 = A_4 × tan\,\alpha_2 = 7,74\,in × tan\,57,46^o = 12.12\,in$$
Finalmente, a calculadora combina os valores acima calculados para calcular o comprimento total dos passos:
$Stringer\,Length = C_3 + B_3 + (Número\,de\,Passos – 1) × (B_1 + C_2) = 9.33\,in + 2,72\,in + (16-1) × (3,8\,in + 9,32\,in) = 208,88\,in$
Cálculos de montagem embutida

p>Calculando a subida, corrida, ângulo e comprimento de stringer para uma montagem embutida é muito semelhante à montagem padrão.
Lembramos simplesmente que o passo final nos leva ao decking.
Como antes, calculamos a subida vertical:
$Subida = {Total\,Subida Número,de\,Passos} = {120\,em 17} = 7.06\,in$$
Não é como a medida padrão de montagem, onde subtraímos o passo final da subida, com uma montagem nivelada temos isso:
$$Rise\,of\,steps = Total\,Rise = 120\,in$
No entanto, no passo superior, não teremos nenhum degrau (porque o passo final é o próprio decking!) Assim, transformamos as fórmulas acima para obter o espaçamento vertical de subida:
$$Rise\,of\,steps = Total\,Rise – Piso,Thickness = 120\,in – 2\,in = 118\,in$
As antes, incluindo o piso ao considerar a corrida dos degraus dá:
$$Run,of,steps = Total\,Run – (Piso,Sobreposição + Riser\,Espessura) = 180\,in – (2\,in + 1\,in) = 177\,in$
Assim, a nossa calculadora calcula a distância horizontal total entre a borda de cada passo.
A diferença aqui é que temos 17 passos, uma vez que o passo final está incluído na montagem nivelada!
$Run = {Run\,of\,steps \over Número\,of\,steps} = {177,in \over 17} = 10.41\,in$
Considerando um único passo, a distância horizontal total será dada por:
$Total\,Horizontal\,Distância = Correr + Piso\,Sobreposição + Riser\,Espessura = 10.41,in + 2,in + 1,in = 13.41,in$
E o ângulo entre a horizontal e a escada é mais uma vez dado por:
$tan,|alpha_1 = {Subida,de,degraus {\a1} → {\a1} {\a1} = tan^{-1} {Subida,de,degraus {\a1} = tan^{-1} {120,in + 177,in} = 34.14^o$
Calcular o comprimento da corda é o mesmo método que para a montagem padrão.
A calculadora calcula primeiro os ângulos:
 /p>
/p>
$$_2 = 90^o – \alfa_1 = 90^o – 34,14^o = 55,86^o$$
$$=3 = 90^o + \alfa_2 = 90^o + 55.86^o = 145.86^o$$
$$$=4 = \alfa_1 = 34.14^o$$
$$\alfa_5 = 90^o + \alfa_1 = 90^o + 34.14^o = 124.14^o$$
E a calculadora calcula o espaçamento para os comprimentos como antes:

$A_1 = Ascensão × pecado\,\alpha_2 = 7.06\,in × sin\,55.86^o = 5.84\,in$$
$A_2 = Stringer\,Width – A_1 = 12\,in – 5.84\,in = 6.16\,in$
$C_2 = \sqrt{Run^2 – {A_1}^2} = \sqrt{(10.41\,in)^2 – (5.84\,in)^2} = 8.62\,in$
$C_3 = A_1 × tan\,\alpha_2 = 5.84\,in × tan\,55.86^o = 8.62\,in$$
$B_1 = \sqrt{Rise^2 – {A_1}^2} = \sqrt{(7.06\,in)^2- (5.84\,in)^2} = 3.96\,in$
$B_2 = A_2 × tan\,\alfa_1 = 6.16\,in × tan\,34.14^o = 4.17\,in$
$B_3 = (Ascensão -Tread\,Espessura) × cos\,\alpha_2 = (7.06\,in – 2\,in) × cos\,55.86^o = 2,84\,in$
$A_3 = (Elevação -Pisa – Espessura) × cos\,\alfa_1 = (7,06\,in – 2\,in) × cos\,34.14^o = 4,19\,in$
$A_4 = Stringer\,Largura – A_3 = 12\,in – 4,19\,in = 7,81\,in$
$C_4 = A_4 × tan\,\alpha_2 = 7.81\,in × tan\,55.86^o = 11.52\,in$
Finalmente, a calculadora calcula o comprimento total de stringer como antes:
$Stringer\,Length = C_3 + B_3 + (Número\,de\,passos – 1) × (B_1 + C_2) = 8.62\,in + 2,84\,in + (17-1) × (3,96\,in + 8,62\,in) = 212,72\,in$
Cuidado! ⚠️
Cuidado de não arredondar a sua resposta antes do cálculo final. Estes pequenos erros de arredondamento podem ter uma grande diferença na resposta final!
Compreendemos que isto é bastante difícil de seguir! Fique descansado, se não compreender isto, não se preocupe.
A calculadora faz tudo isto por si, mudando a ênfase e a preocupação de si para a tecnologia. 😉
Perguntas Frequentemente Feitas
- Que orientações ou regulamentos tenho de considerar ao planear a construção de um conjunto de escadas?
Recomendamos que esteja ciente de todos os regulamentos de construção no seu país de origem.
A nossa calculadora está programada para dar medições precisas dentro da orientação do Council of American Building Officials and International Code Council.
- >li> Quais as propriedades que devem cumprir os regulamentos de construção do meu país de origem para escadas e escadarias?
Você deve verificar com os regulamentos de construção do seu país de origem para uma resposta exacta.
No entanto, um bom guia é que qualquer empresa ou igreja, organização, escritório ou propriedade comercial deve cumprir as normas de escadas do seu país de origem.
Seja cuidadoso – abre-se a potenciais multas substanciais se não cumprir os padrões das escadas.
Utilize a nossa calculadora, faça alguma pesquisa e siga os exemplos acima para se certificar de que os está a cumprir antes de começar!
- E se as minhas medidas de escadas estiverem noutras unidades métricas ou imperiais?
A resposta é muito simples! A nossa calculadora pode trabalhar em muitas unidades diferentes ao mesmo tempo.
O estimador faz as conversões por si usando os seguintes rácios:
$1\,foot = 12\,inches = 0.33\,jardas = 30,48\,centímetros = 0,3048\,metros$
É assim tão fácil! 🙂
- li> As minhas escadas de casa têm de cumprir as normas de governação locais?
Não! Como regra geral, as normas de regulamentação da construção de escadas são aplicáveis a propriedades comerciais que utilizam escadas permanentes, e não aos degraus típicos da casa, temporários ou portáteis para uso pessoal.
- Existe alguma orientação ou conselho sobre quanto tempo as minhas escadas devem ter?
Uma boa orientação é dada pelo Council of American Building Officials e pelo International Code Council.
Estes regulamentos recomendam que a subida das escadas não seja superior a 7,75 polegadas (17,78 cm) e que a escada não seja inferior a 10 polegadas (25 polegadas).4 cm).
Não se esqueça, porém, que isto é para uma propriedade comercial.
Isto pode não ser prático ou necessário para a sua casa, onde as suas escadas não têm de cumprir as mesmas normas comerciais, mas devem ser utilizadas como um guia.
- li> Onde posso encontrar mais informações sobre as normas das escadas para propriedades comerciais?
Há muita informação que pode ser encontrada online.
Recomendamos este website como um óptimo ponto de partida: https://codes.iccsafe.org/content/IBC2018P4/chapter-10-means-of-egress#IBC2018P4_Ch10_Sec1011. A secção 1011 tem muita informação do código de construção internacional de 2018.