O modelo de espaço estatal do sistema Linear de Variação Temporal (LTI) pode ser representado como,
$$$$$$$$/p>
$$Y=CX+DU$$
A primeira e a segunda equações são conhecidas como equação de estado e equação de saída, respectivamente.
Onde,
-
X e $\dot{X}$ são o vector de estado e o vector de estado diferencial, respectivamente.
-
U e Y são respectivamente o vector de entrada e o vector de saída.
-
A é a matriz do sistema.
- p>B e C são as matrizes de entrada e de saída.
- p>D é a matriz de avanço.
Conceitos Básicos do Modelo Espacial do Estado
A seguinte terminologia básica envolvida neste capítulo.
State
É um grupo de variáveis, que resume a história do sistema de modo a prever os valores futuros (outputs).
Variável de Estado
O número de variáveis de estado requerido é igual ao número de elementos de armazenamento presentes no sistema.
Exemplos – corrente fluindo através do indutor, tensão através do condensador
Vector de Estado
É um vector, que contém as variáveis de estado como elementos.
Nos capítulos anteriores, discutimos dois modelos matemáticos dos sistemas de controlo. Estes são o modelo da equação diferencial e o modelo da função de transferência. O modelo do espaço de estados pode ser obtido a partir de qualquer um destes dois modelos matemáticos. Vamos agora discutir estes dois métodos um por um.
Modelo de Espaço de Estado da Equação Diferencial
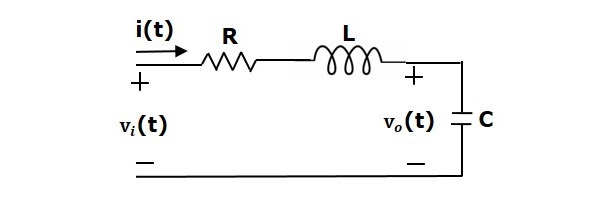
Existem dois elementos de armazenamento (indutor e condensador) neste circuito. Assim, o número de variáveis de estado é igual a dois e estas variáveis de estado são a corrente que flui através do indutor, $i(t)$ e a tensão através do condensador, $v_c(t)$.
Do circuito, a tensão de saída, $v_0(t)$ é igual à tensão através do condensador, $v_c(t)$.
$$v_0(t)=v_c(t)$
Aplicar KVL em torno do circuito.
$$v_i(t)=Ri(t)+L\frac{\i(t)}{d}i(t)}{texto{d}t}+v_c(t)$
$$$$frac{d}i(t)}{d(t)}{d(t)}{d\Frac{Ri(t)}{L}-frac{v_c(t)}{L}+frac{v_i(t)}{L}$$
A voltagem através do condensador é –
$v_c(t)==frac{1}{C} \int i(t) dt$
Diferencie a equação acima com respeito ao tempo.
$$frac{\i(d)}v_c(t)}{\i(t)}=frac{i(t)}{C}$$
State vector, $X==begin{bmatrix}i(t) {v_c(t) {bmatrix}$
Diferencial vector de estado, $dot{X}=begin{bmatrix{bmatrix}frac{d(t)}text{d(t){d(t)t} \\\frac{\text{d}v_c(t)}{\text{d}t} \{bmatrix}$
Podemos organizar as equações diferenciais e a equação de saída na forma padrão do modelo espacial de estado como,
$Y==begin{bmatrix}0 & 1 {bmatrix}begin{bmatrix}i(t) {v_c(t) {bmatrix}$
Onde,
State Space Model from Transfer Function
Considerar os dois tipos de funções de transferência com base no tipo de termos presentes no numerador.
- Função de transferência com termo constante no Numerador.
- Função de transferência com função polinomial de ‘s’ no Numerador.
Função de transferência com termo constante em Numerador
Considerar a seguinte função de transferência de um sistema
$$\frac{Y(s)}{U(s)}=\frac{b_0}{s^n+a_{n-1}s^{n-1}+…+a_1s+a_0}$$
Reorganizar, a equação acima como
$(s^n+a_{n-1}s^{n-1}+…+a_0)Y(s)=b_0 U(s)$
Aplicar a transformação Laplace inversa em ambos os lados.
$\frac{\text{d}^ny(t)}{\text{d}t^n}+a_{n-1}\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}+…+a_1\frac{\frac{d}y(t)}{\frac{d}t}+a_0y(t)=b_0 u(t)$
Let
$$y(t)=x_1$
$\frac{\text{d}y(t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2y(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}y(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^ny(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then,
$\dot{x}_n+a_{n-1}x_n+…+a_1x_2+a_0x_1=b_0 u$
Da equação acima, podemos escrever a seguinte equação de estado.
$$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+b_0 u$
A equação de saída é –
$$y(t)=y=x_1$
O modelo de espaço de estados é –
$$dot{X}=begin{bmatrix}_1dot{x}_1 {x}_2 {x}vdots {x}_dot{x1}dot{x}_n {bmatrix}$
$$Y=\begin{bmatrix}1 && \& 0 & 0 {bmatrix}{begin{bmatrix}x_1 {bmatrix}x_2 {n-1}x_n {bmatrix}$
Aqui, $D==esquerda .$
Exemplo
P>Encontrar o modelo de espaço estatal para o sistema com função de transferência.
$$frac{Y(s)}{U(s)}==frac{1}{s^2+s+1}$$
Reorganizar, a equação acima como,
$(s^2+s+1)Y(s)=U(s)$$
Aplicar a transformação Laplace inversa em ambos os lados.
$$frac{\i}{d}^2y(t)}{\i(t)^2y(t)}{d)t^2}+frac{d}y(t)}{d(t)=u(t)$
Let
$$y(t)=x_1$$
$$frac{\i}{d}y(t)}{\i(t)}=x_2==dot{x}_1$
and $u(t)=u$
Então, a equação de estado é
$$$t{x}_2=-x_1-x_2+u$
A equação de saída é
$y(t)=y=x_1$$
O modelo de espaço de estados é
$Y=\begin{bmatrix}1 & 0 {bmatrix}\begin{bmatrix}x_1 {bmatrix}x_2 \{bmatrix}$$
Função de transferência com função polinomial de ‘s’ em Numerador
Considerar a seguinte função de transferência de um sistema
$$frac{Y(s)}{U(s)}=\frac{b_n s^n+b_{n-1}s^{n-1}+…+b_1s+b_0}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$$
$$$\A direita \frac{Y(s)}{U(s)}=esquerda( \frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}direita )(b_n s^n+b_{n-1}s^{n-1}+….+b_1s+b_0)$
A equação acima está na forma de produto de funções de transferência de dois blocos, que são em cascata.
$$frac{Y(s)}{U(s)}=esquerda(U(s)}{V(s)}{U(s)}{U(s)} \i1}right ) \esquerda(s)(s){Y(s)}{V(s)}{V(s)} \{V(s)}{U(s)}==frac{1}{s^n+a_{n-1}s^{n-1}+…+a_1 s+a_0}$$
$$frac{V(s)}{U(s)}==frac{1}{s^n+a_{n-1}s^{n-1}+…+a_0)V(s)=U(s)$$
Aplique a transformação inversa de Laplace em ambos os lados.
$$frac{\i}{d}^nv(t)}{\i}{\i}{\i}{\i}{n-1}frac{\i}+a_{n-1}frac{\i}{n-1}v(t)}{\i}{n-1}t^{n-1}+…+a_1 {\frac{\d}v(t)}{\d(t)}+a_0v(t)=u(t)$
Let
$v(t)=x_1$
$\frac{\text{d}v((t)}{\text{d}t}=x_2=\dot{x}_1$
$\frac{\text{d}^2v(t)}{\text{d}t^2}=x_3=\dot{x}_2$
$\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}=x_n=\dot{x}_{n-1}$
$\frac{\text{d}^nv(t)}{\text{d}t^n}=\dot{x}_n$
and $u(t)=u$
Then, a equação de estado é
$$$\dot{x}_n=-a_0x_1-a_1x_2-…-a_{n-1}x_n+u$
Consider,
$\frac{Y(s)}{V(s)}=b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0$$
Reorganizar, a equação acima como
$Y(s)=(b_ns^n+b_{n-1}s^{n-1}+…+b_1s+b_0)V(s)$
Aplicar a transformação Laplace inversa em ambos os lados.
$y(t)=b_n\frac{\text{d}^nv(t)}{\text{d}t^n}+b_{n-1}\frac{\text{d}^{n-1}v(t)}{\text{d}t^{n-1}}+…+b_1}frac{\frac{d}v(t)}{\text{d}t}+b_0v(t)$
Ao substituir as variáveis de estado e $y(t)=y$ na equação acima, obterá a equação de saída como,
$y=b_n\dot{x}_n+b_{n-1}x_n+…+b_1x_2+b_0x_1$$
Substituto, $\dot{x}_n$ valor na equação acima.
$y=b_n(-a_0x_1-a_1x_2-…-a_{n-1}x_n+u)+b_{n-1}x_n+…+b_1x_2+b_0x_1$
$y=(b_0-b_na_0)x_1+(b_1-b_na_1)x_2+…+(b_{n-1}-b_na_{n-1})x_n+b_n u$
O modelo espacial estatal é
$$dot{X}=begin{bmatrix}=dot{x}_1 {x}_2 {x}_vdot{x}_dot{x1}dot{x_n {bmatrix}$
$$Y==begin{bmatrix}x_1 {x_2 {n-1}vdots {n-1}x_n {bmatrix}$
If $b_n = 0$, então,
$$Y=\begin{bmatrix}x_1 \x_2 {n-1}vdots \x_{n-1} \x_n {bmatrix}$