![]()
![]()

A distribuição binomial dá a distribuição discreta de probabilidade ![]() de obter exactamente
de obter exactamente ![]() êxitos de
êxitos de ![]() ensaios Bernoulli (onde o resultado de cada ensaio Bernoulli é verdadeiro com probabilidade
ensaios Bernoulli (onde o resultado de cada ensaio Bernoulli é verdadeiro com probabilidade ![]() e falso com probabilidade
e falso com probabilidade ![]() ). A distribuição binomial é portanto dada por
). A distribuição binomial é portanto dada por
|
(1)
|
|||
|
(2)
|
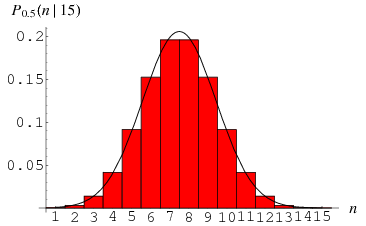
where ![]() é um coeficiente binomial. O gráfico acima mostra a distribuição de
é um coeficiente binomial. O gráfico acima mostra a distribuição de ![]() êxitos de
êxitos de ![]() ensaios com
ensaios com ![]() .
.
p> A distribuição binomial é implementada na Linguagem Wolfram como BinomialDistribuição.
A probabilidade de obter mais sucessos do que o ![]() observado numa distribuição binomial é
observado numa distribuição binomial é
|
(3)
|
where
|
(4)
|
![]() é a função beta, e
é a função beta, e ![]() é a função beta incompleta.
é a função beta incompleta.
A função característica para a distribuição binomial é
|
(5)
|
(Papoulis 1984, p. 154). O momento…função geradora ![]() para a distribuição é
para a distribuição é
|
(6)
|
|||
|
(7)
|
|||
|
(8)
|
|||
|
(9)
|
|||
|
(10)
|
|||
|
(11)
|
A média é
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
Os momentos cerca de 0 são
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
|||
|
(18)
|
sob os momentos sobre o meanare
|
(19)
|
|||
|
(20)
|
|||
|
(21)
|
A skewness e o kurtosisexcess são
|
(22)
|
|||
|
(23)
|
|||
 |
(24)
|
||
|
(25)
|
O primeiro cumulante é
|
(26)
|
e os cumulantes subsequentes são dado pela recurrencerelação
|
(27)
|
The o desvio médio é dado por
|
(28)
|
Para o caso especial ![]() , isto é igual a
, isto é igual a
|
(29)
|
|||
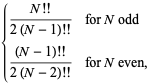 |
(30)
|
where ![]() é um factorial duplo. Para
é um factorial duplo. Para ![]() , 2, …, os primeiros valores são portanto 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 e A086117). O caso geral é dado por
, 2, …, os primeiros valores são portanto 1/2, 1/2, 3/4, 3/4, 15/16, 15/16, … (OEIS A086116 e A086117). O caso geral é dado por
|
(31)
|
Steinhaus (1999, pp. 25-28) considera o número esperado de quadrados ![]() contendo um dado número de grãos
contendo um dado número de grãos ![]() a bordo de tamanho
a bordo de tamanho ![]() após distribuição aleatória de
após distribuição aleatória de ![]() de grãos,
de grãos,
|
(32)
|
Taking ![]() dá os resultados resumidos na tabela seguinte.
dá os resultados resumidos na tabela seguinte.
| 0 | 23.3591 |
| 1 | 23.7299 |
| 2 | 11.8650 |
| 3 | 3.89221 |
| 4 | 0.942162 |
| 5 | 0.179459 |
| 6 | 0.0280109 |
| 7 | 0.0036840 |
| 8 | |
| 9 | |
| 10 | |
Uma aproximação à distribuição binomial para grandes ![]() pode ser obtido através da expansão sobre o valor
pode ser obtido através da expansão sobre o valor ![]() onde
onde ![]() é um máximo, i.e., onde
é um máximo, i.e., onde ![]() . Uma vez que a função logarítmica é monotónica, podemos, em vez disso, optar por expandir o logaritmo. Let
. Uma vez que a função logarítmica é monotónica, podemos, em vez disso, optar por expandir o logaritmo. Let ![]() , then
, then
|
(33)
|
where
|
(34)
|
Mas estamos a expandir ao máximo, portanto, por definição,
|
(35)
|
Isto também significa que ![]() é negativo, para que possamos escrever
é negativo, para que possamos escrever ![]() . Agora, tomando o logaritmo de (◇) dá
. Agora, tomando o logaritmo de (◇) dá
|
(36)
|
Para grande ![]() e
e ![]() podemos usar a aproximação de Stirling
podemos usar a aproximação de Stirling
|
(37)
|
so
|
(38)
|
|||
|
(39)
|
|||
|
(40)
|
|||
|
(41)
|
|||
|
(42)
|
and
|
(43)
|
Para encontrar ![]() , definir esta expressão para 0 e resolver para
, definir esta expressão para 0 e resolver para ![]() ,
,
|
(44)
|
|
(45)
|
|
(46)
|
|
(47)
|
desde ![]() . Podemos agora encontrar os termos na expansão
. Podemos agora encontrar os termos na expansão
|
(48)
|
|||
|
(49)
|
|||
|
(50)
|
|||
|
(51)
|
|||
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
|||
|
(55)
|
|||
|
(56)
|
|||
|
(57)
|
|||
|
(58)
|
|||
|
(59)
|
Agora, tratando a distribuição como contínua,
|
(60)
|
Desde que cada termo seja de ordem ![]() menor que o anterior, podemos ignorar termos superiores a
menor que o anterior, podemos ignorar termos superiores a ![]() , so
, so
|
(61)
|
A probabilidade deve ser normalizada, so
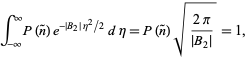 |
(62)
|
and
|
(63)
|
|||
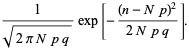 |
(64)
|
Definindo ![]() ,
,
|
(65)
|
que é uma distribuição normal. A distribuição binomial é portanto aproximada por uma distribuição normal para qualquer distribuição fixa ![]() (mesmo que
(mesmo que ![]() seja pequena) como
seja pequena) como ![]() seja levada ao infinito.
seja levada ao infinito.
se ![]() e
e ![]() de tal forma que
de tal forma que ![]() , então a distribuição binomial converge para a distribuição de Poisson com média
, então a distribuição binomial converge para a distribuição de Poisson com média ![]() .
.
p>Let ![]() e
e ![]() ser variáveis binomiais aleatórias independentes caracterizadas por parâmetros
ser variáveis binomiais aleatórias independentes caracterizadas por parâmetros ![]() e
e ![]() . A probabilidade condicional de
. A probabilidade condicional de ![]() dado que
dado que ![]() é
é
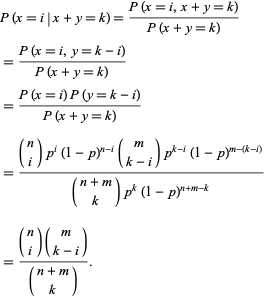 |
(66)
|
Nota que esta é uma distribuição hipergeométrica.